Содержание
- 2. Если множество рациональных чисел дополнить множеством иррациональных чисел, то вместе они составят множество действительных чисел Это
- 3. Каждое действительное число можно изобразить точкой на координатной прямой. Каждая точка координатной прямой имеет действительную координату.
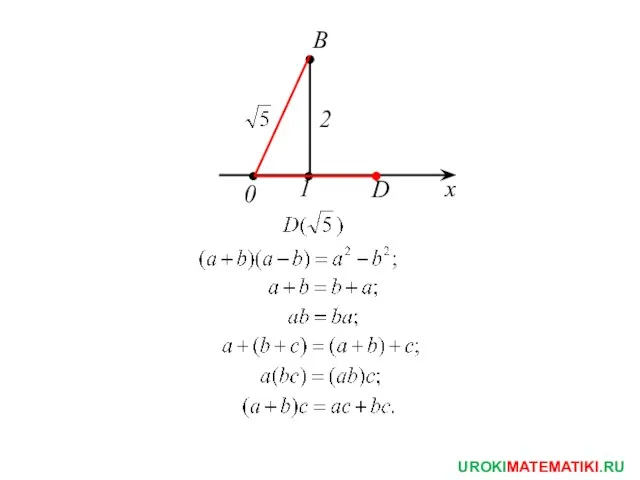
- 4. 0 x 1 B 2 D UROKIMATEMATIKI.RU
- 5. Произведение (частное) двух положительных чисел — положительное число Произведение (частное) двух отрицательных чисел — положительное число
- 6. Определение. Действительное число а больше (меньше) действительного числа b, если их разность a-b — положительное (отрицательное)
- 7. а больше нуля или равно нулю, т.е. а — неотрицательное число (положительное или 0), или что
- 8. Пример 1: Сравнить числа: UROKIMATEMATIKI.RU Игорь Жаборовский © 2012
- 10. Скачать презентацию






 Итоговый урок физика8 класс
Итоговый урок физика8 класс Кто знает обо всём
Кто знает обо всём Дизайн как вид изобразительного искусства
Дизайн как вид изобразительного искусства Разработка домашнего задания на тему: матрешка
Разработка домашнего задания на тему: матрешка Аймактардын социалдык-экономикалык ?н?г?? тенденциясы
Аймактардын социалдык-экономикалык ?н?г?? тенденциясы Программа модернизации системы среднего профессионального образования Республики Карелия
Программа модернизации системы среднего профессионального образования Республики Карелия Ну-ка, проверь-ка, дружок, Ты готов начать урок? Всё ль на месте, всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? Вс
Ну-ка, проверь-ка, дружок, Ты готов начать урок? Всё ль на месте, всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? Вс HTML Первые шаги.
HTML Первые шаги. Формы сохранения культурного наследия
Формы сохранения культурного наследия Выбирай банк смолоду: предложение Райффайзенбанка для молодёжи от команды Giants
Выбирай банк смолоду: предложение Райффайзенбанка для молодёжи от команды Giants Месяц тотального рекрутинга. Только в апреле каждому новичку КЭШБЭК 10%
Месяц тотального рекрутинга. Только в апреле каждому новичку КЭШБЭК 10% Типичные задачи по математике
Типичные задачи по математике Анимация кроссвордовколлективное творчество участников сообщества "ИКТ в НШ"
Анимация кроссвордовколлективное творчество участников сообщества "ИКТ в НШ"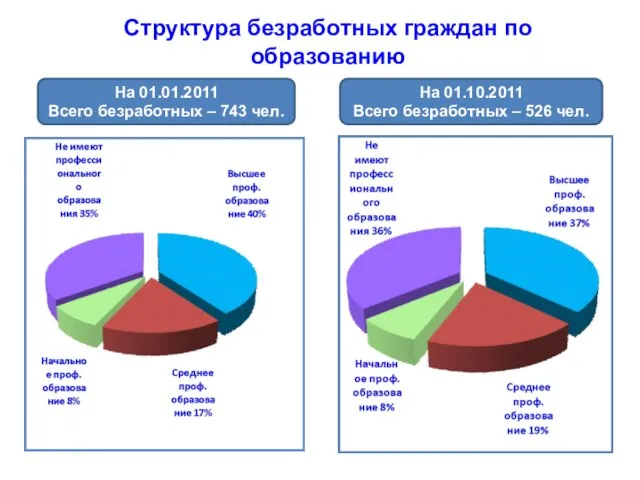 Структура безработных граждан по образованию
Структура безработных граждан по образованию Дистанционный Кадавер курс
Дистанционный Кадавер курс Оценка безопасности комбинации индометацина и тиотриазолина по влиянию на слизистую желудка
Оценка безопасности комбинации индометацина и тиотриазолина по влиянию на слизистую желудка Линии одним росчерком пера
Линии одним росчерком пера Political System of Kazakhstan
Political System of Kazakhstan  Семья Яковлевых прдставляет
Семья Яковлевых прдставляет История расчески
История расчески Какими средствами воздействует искусство? 7 класс
Какими средствами воздействует искусство? 7 класс Физика и искусство
Физика и искусство Как общаться с подростком
Как общаться с подростком Как посвятить учеников в ряды пятиклассников
Как посвятить учеников в ряды пятиклассников 20140928_dimova_v.m.priem_rabota_s_risunkami._tektonicheskaya_karta
20140928_dimova_v.m.priem_rabota_s_risunkami._tektonicheskaya_karta Роберт Шуман
Роберт Шуман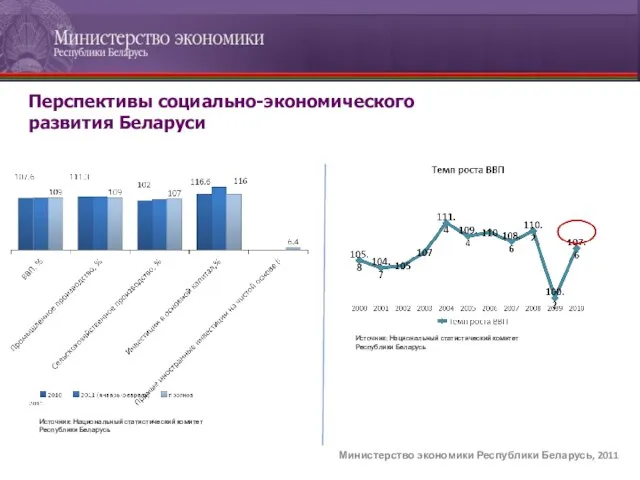 Перспективы социально-экономического развития Беларуси
Перспективы социально-экономического развития Беларуси Презентация на тему Правовой статус таможенного перевозчика
Презентация на тему Правовой статус таможенного перевозчика