02-05

Пересекающиеся прямые
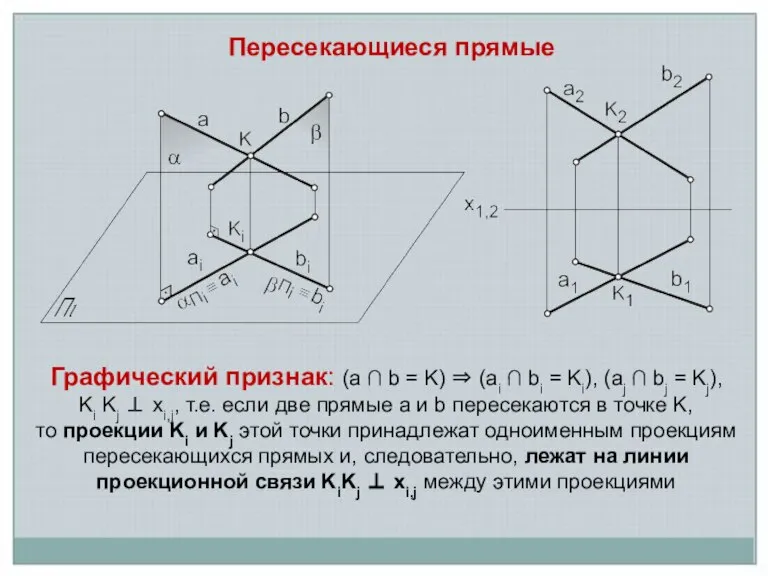
Графический признак: (a ∩ b = K) ⇒ (ai ∩ bi = Ki), (aj ∩ bj = Kj),
Ki Kj ⊥ xi,j, т.е. если две прямые a и b пересекаются в точке K,
то проекции Ki и Kj этой точки принадлежат одноименным проекциям пересекающихся прямых и, следовательно, лежат на линии проекционной связи KiKj ⊥ xi,j между этими проекциями

если одноименные проекции прямых на каждой из плоскостей проекций параллельны между собой,
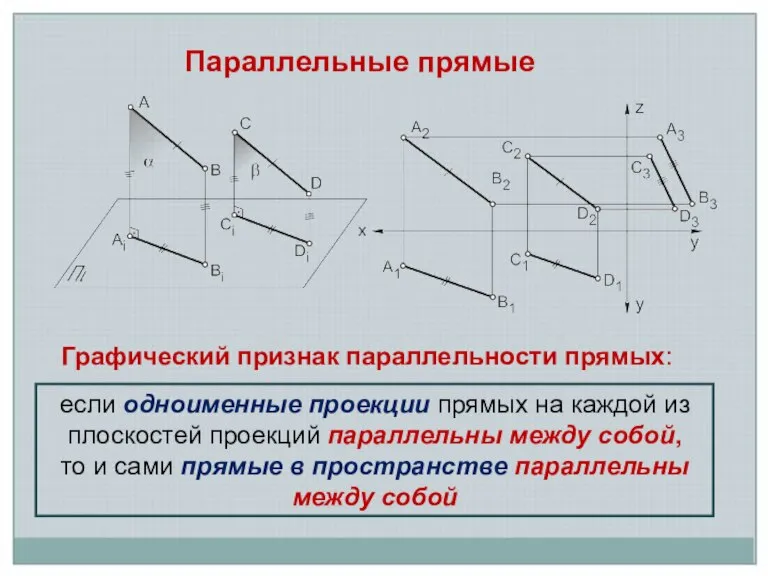
то и сами прямые в пространстве параллельны между собой
Графический признак параллельности прямых:
Параллельные прямые

Скрещивающиеся прямые
Графический признак скрещивающихся прямых:
признак основан на невыполнении признаков параллельности или пересечения таких прямых.
Точки пересечения одноименных проекций на смежных плоскостях не лежат на линии их проекционной связи, а параллельность проекций может иметь место только на одной из плоскостей проекций