Содержание
- 2. The Method of Projection In graphic language the shape is described by projection, which is the
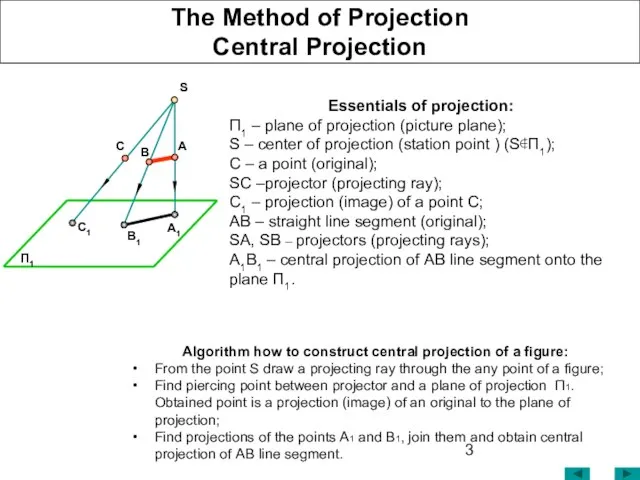
- 3. The Method of Projection Central Projection Essentials of projection: П1 – plane of projection (picture plane);
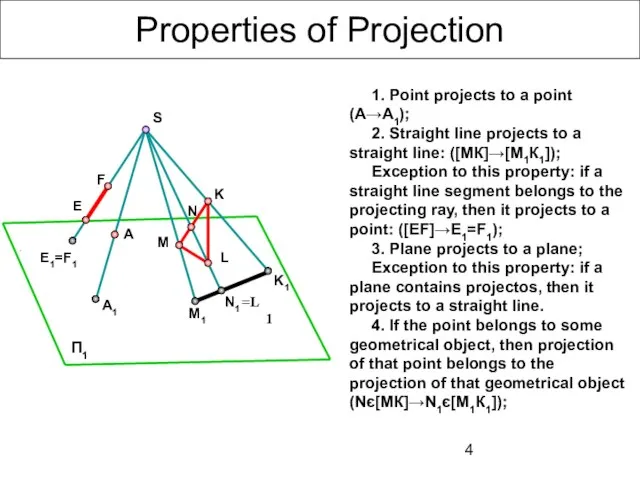
- 4. Properties of Projection 1. Point projects to a point (А→А1); 2. Straight line projects to a
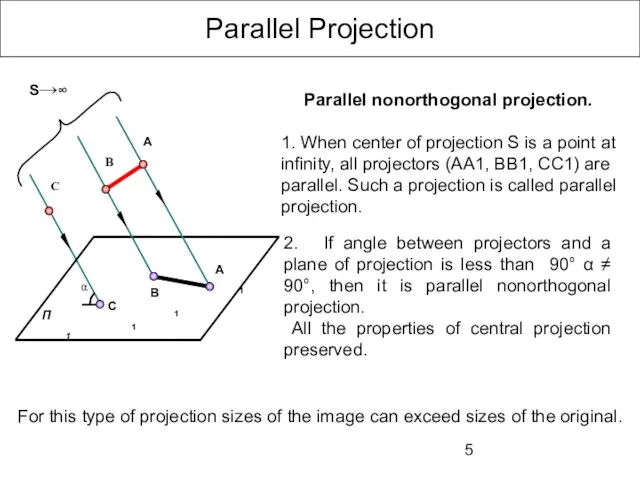
- 5. Parallel Projection 2. If angle between projectors and a plane of projection is less than 90°
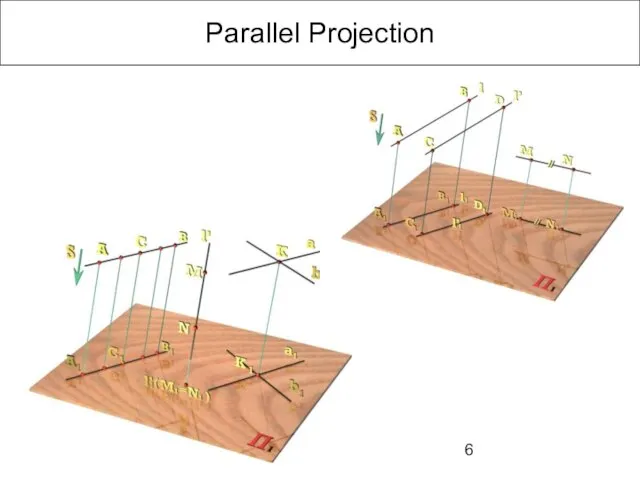
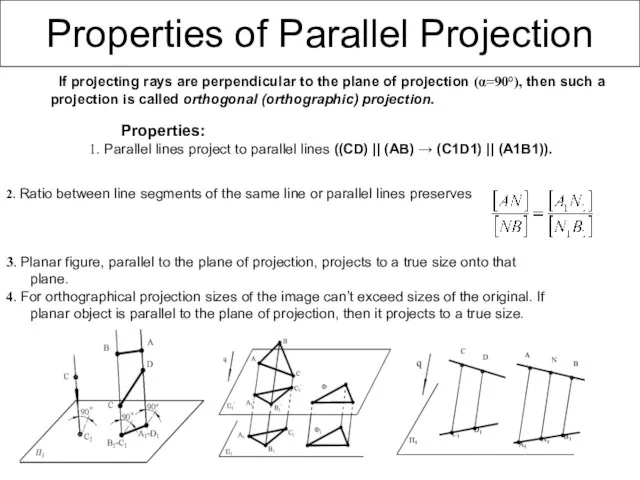
- 6. Parallel Projection
- 7. 2. Ratio between line segments of the same line or parallel lines preserves 3. Planar figure,
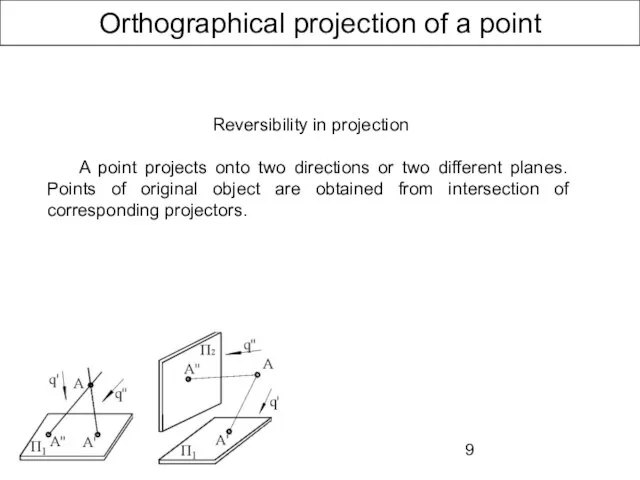
- 8. Orthographical projection of a point Images on the drawings should be reversible to imagine real shape
- 9. Orthographical projection of a point Reversibility in projection A point projects onto two directions or two
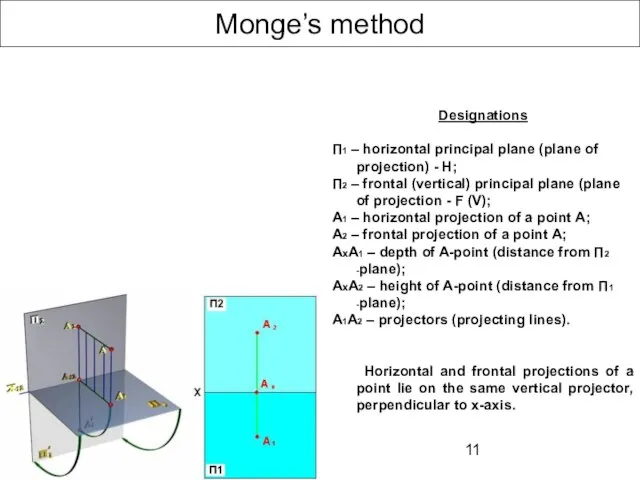
- 10. Monge’s method A point projects onto two mutually perpendicular principal planes (planes of projection). After that
- 11. Monge’s method Designations П1 – horizontal principal plane (plane of projection) - H; П2 – frontal
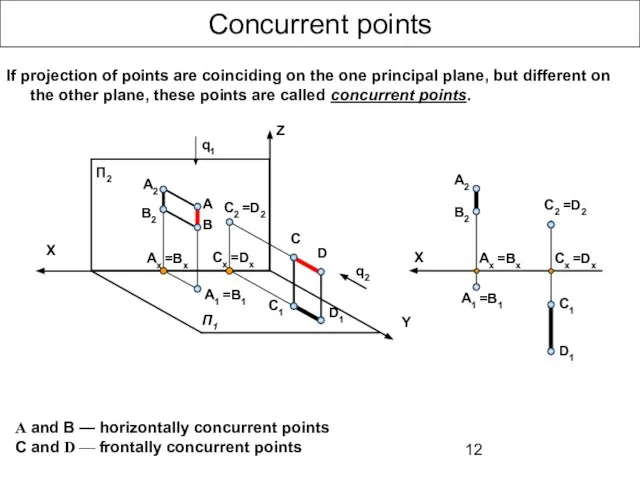
- 12. Concurrent points А and В — horizontally concurrent points C and D — frontally concurrent points
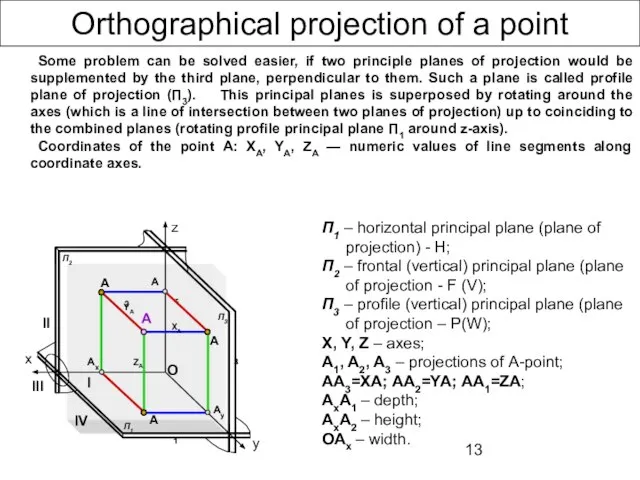
- 13. Orthographical projection of a point Some problem can be solved easier, if two principle planes of
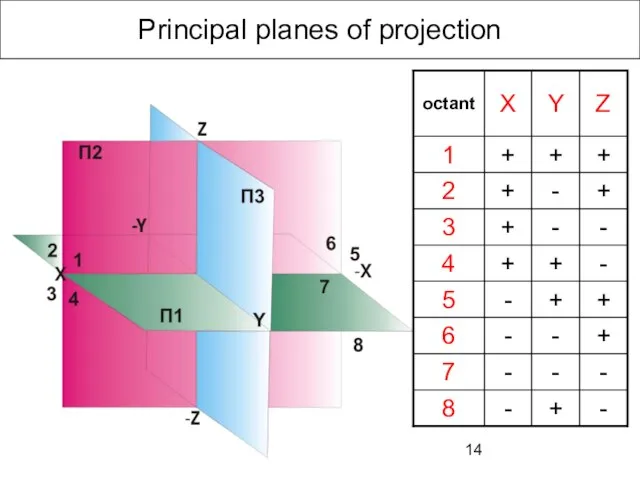
- 14. Principal planes of projection
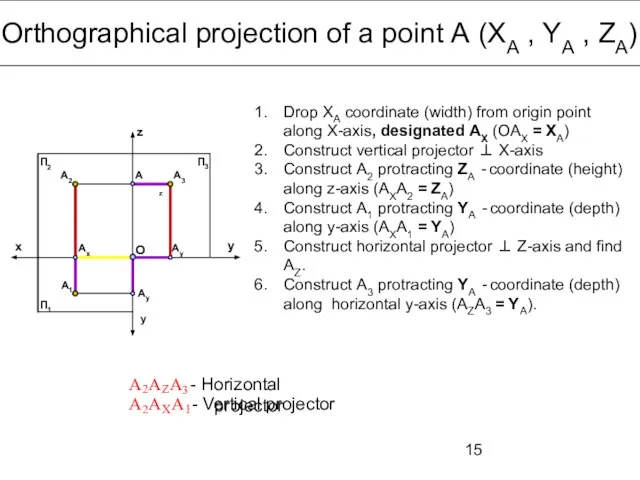
- 15. Orthographical projection of a point А (ХА , YA , ZA) x y z y П1
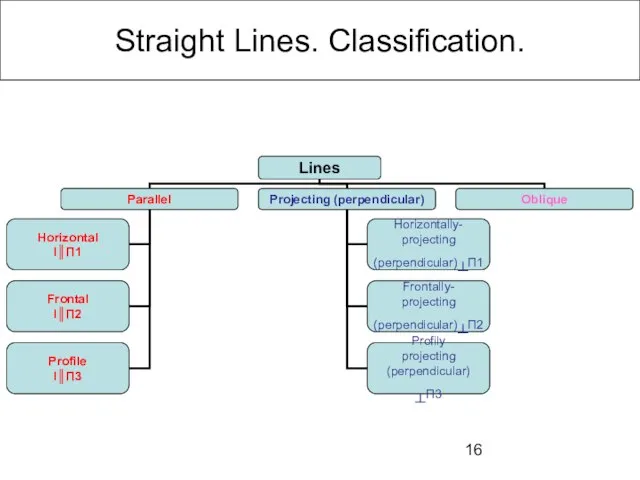
- 16. Straight Lines. Classification.
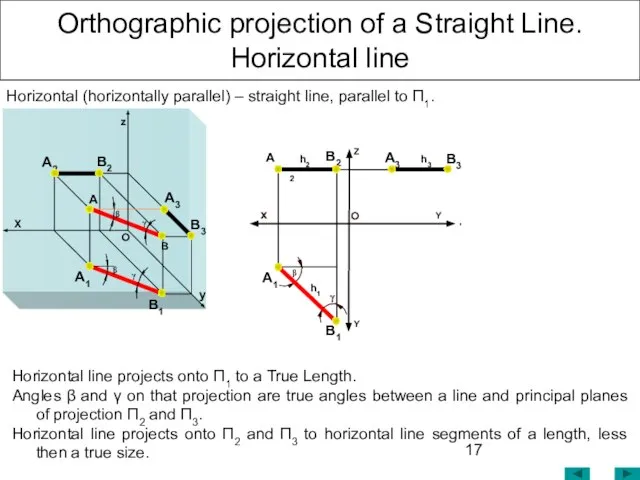
- 17. Orthographic projection of a Straight Line. Horizontal line Horizontal (horizontally parallel) – straight line, parallel to
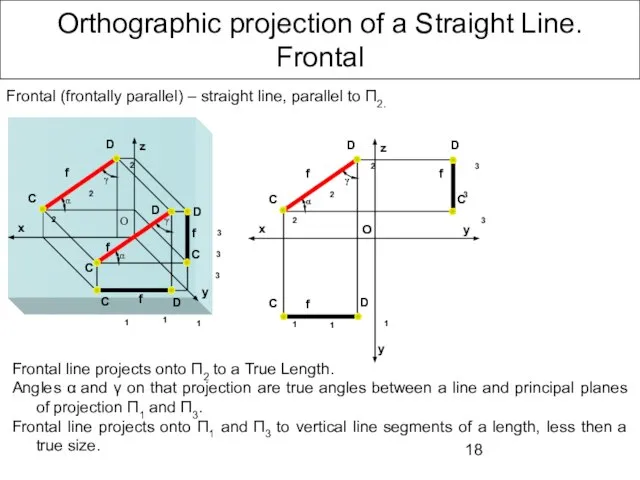
- 18. Orthographic projection of a Straight Line. Frontal Frontal line projects onto П2 to a True Length.
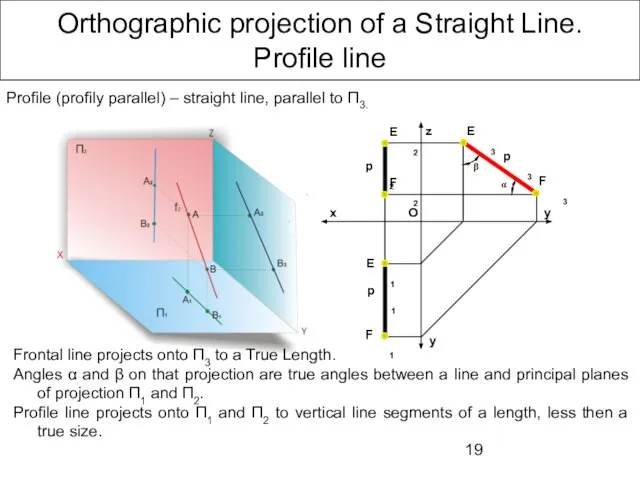
- 19. Orthographic projection of a Straight Line. Profile line Profile (profily parallel) – straight line, parallel to
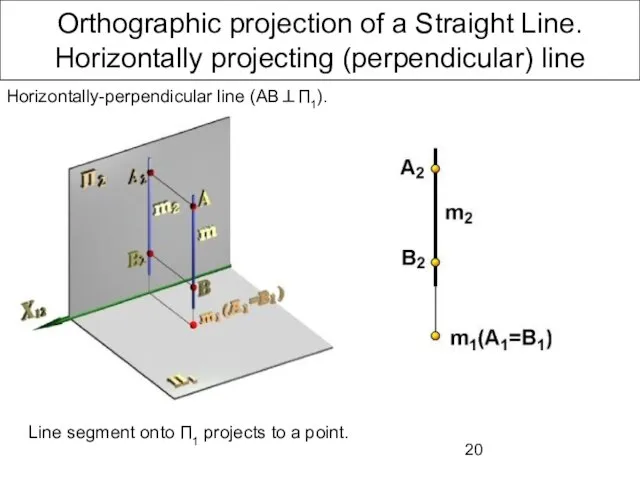
- 20. Orthographic projection of a Straight Line. Horizontally projecting (perpendicular) line Line segment onto П1 projects to
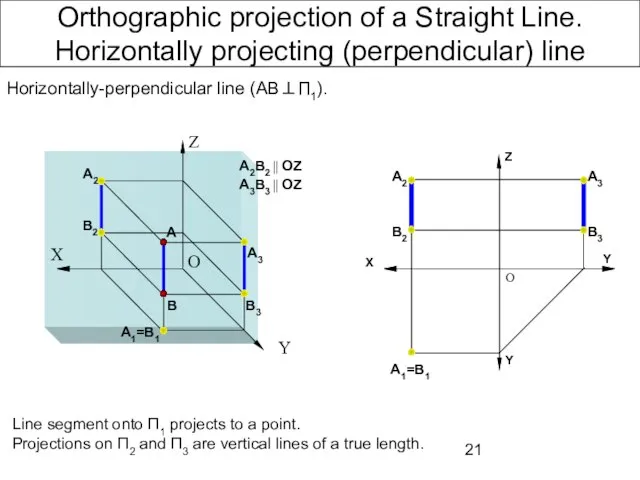
- 21. Orthographic projection of a Straight Line. Horizontally projecting (perpendicular) line Line segment onto П1 projects to
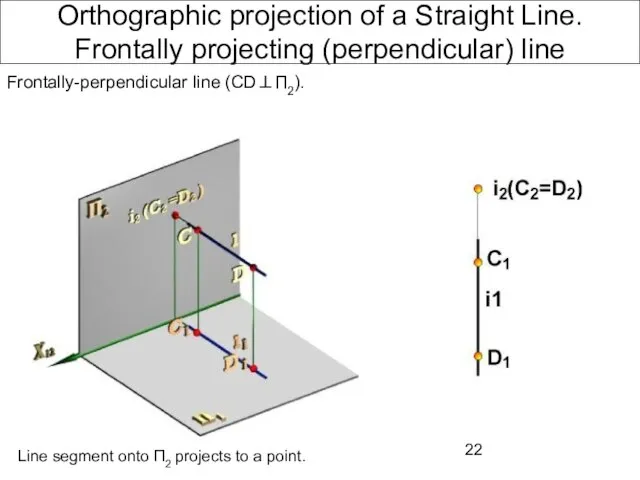
- 22. Orthographic projection of a Straight Line. Frontally projecting (perpendicular) line Frontally-perpendicular line (CD⊥П2). Line segment onto
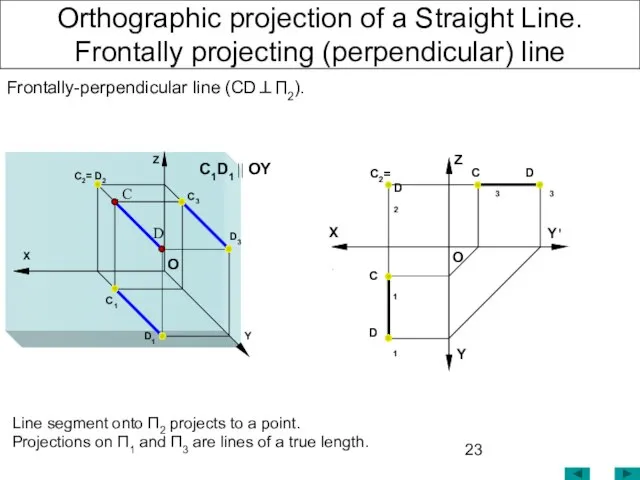
- 23. Orthographic projection of a Straight Line. Frontally projecting (perpendicular) line Frontally-perpendicular line (CD⊥П2). Line segment onto
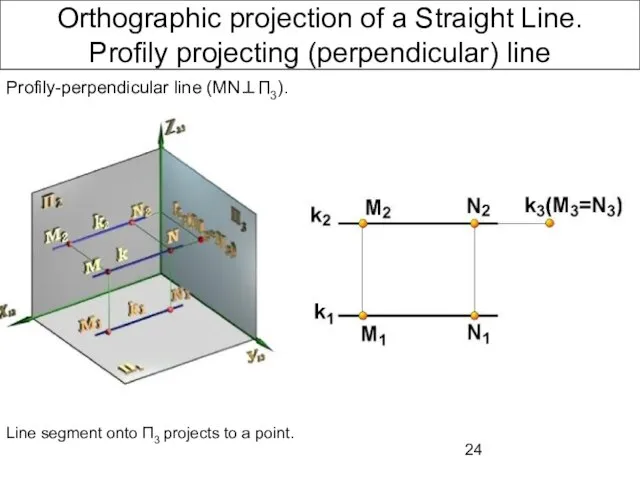
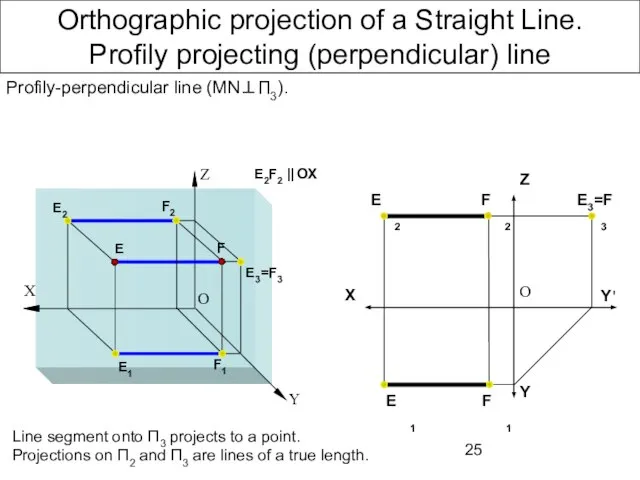
- 24. Orthographic projection of a Straight Line. Profily projecting (perpendicular) line Profily-perpendicular line (MN⊥П3). Line segment onto
- 25. Orthographic projection of a Straight Line. Profily projecting (perpendicular) line Profily-perpendicular line (MN⊥П3). Line segment onto
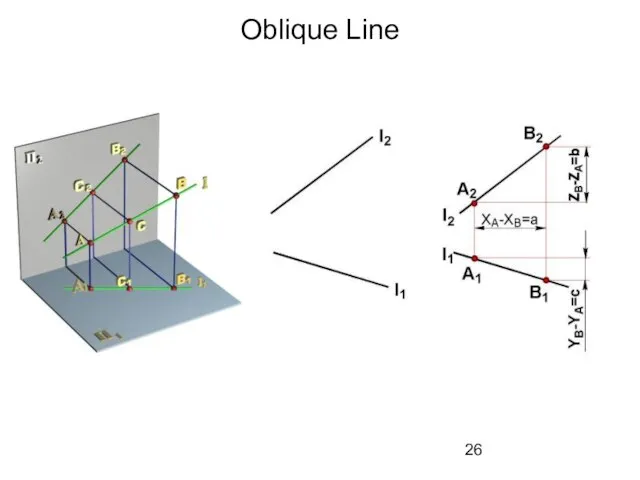
- 26. Oblique Line
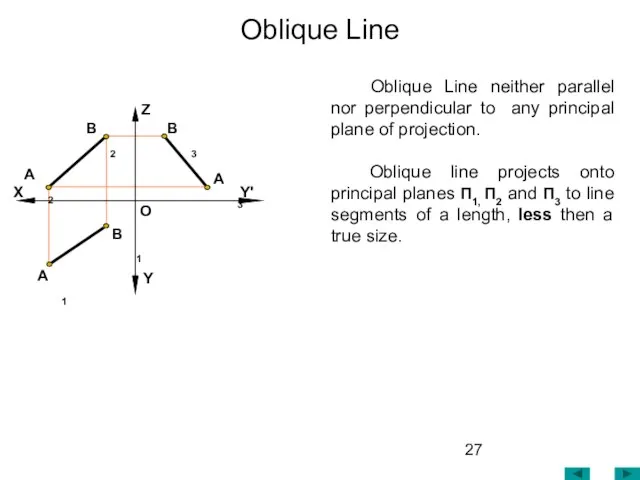
- 27. Oblique Line neither parallel nor perpendicular to any principal plane of projection. Oblique line projects onto
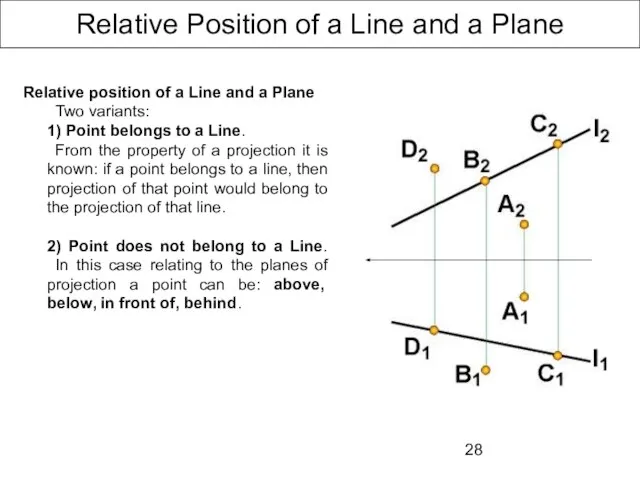
- 28. Relative Position of a Line and a Plane Relative position of a Line and a Plane
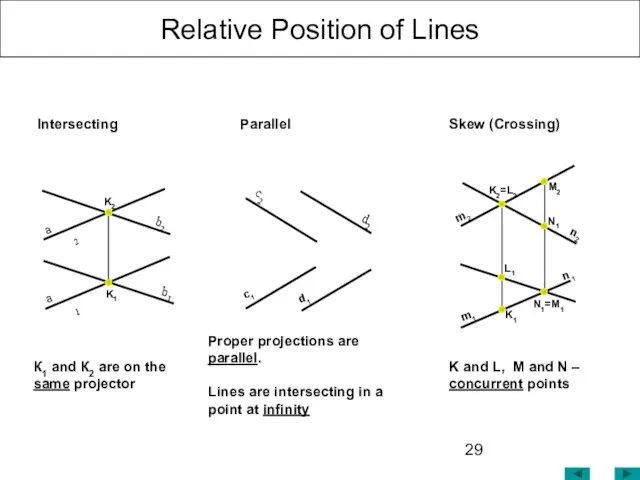
- 29. Relative Position of Lines K and L, M and N – concurrent points Proper projections are
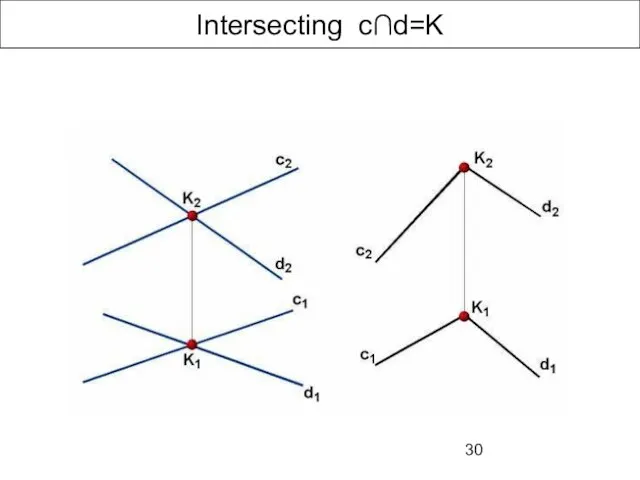
- 30. Intersecting с∩d=K
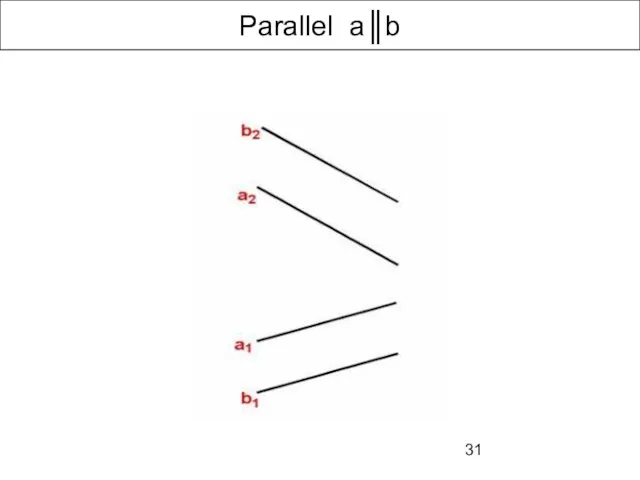
- 31. Parallel a║b
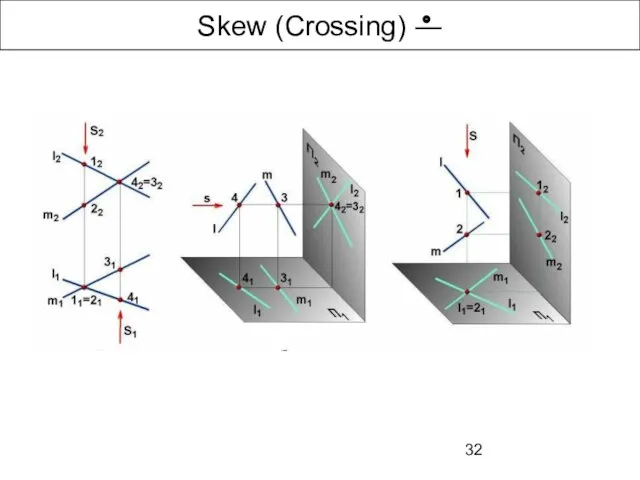
- 32. Skew (Crossing) ―
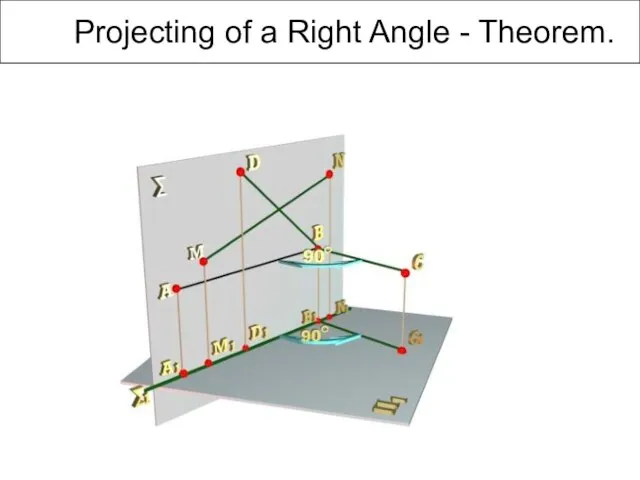
- 33. Projecting of a Right Angle - Theorem.
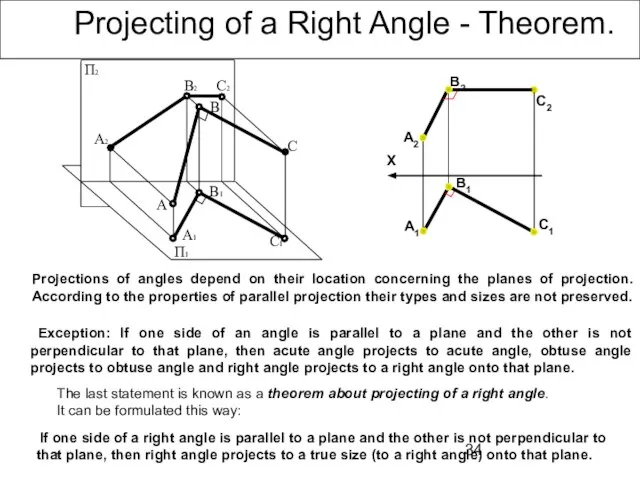
- 34. Projecting of a Right Angle - Theorem. Exception: If one side of an angle is parallel
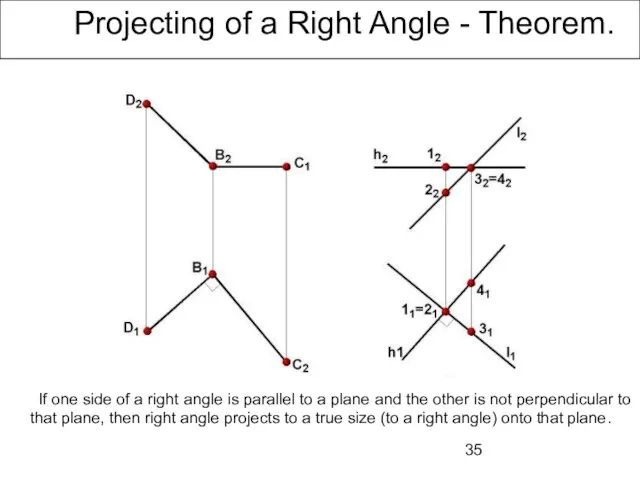
- 35. Projecting of a Right Angle - Theorem. If one side of a right angle is parallel
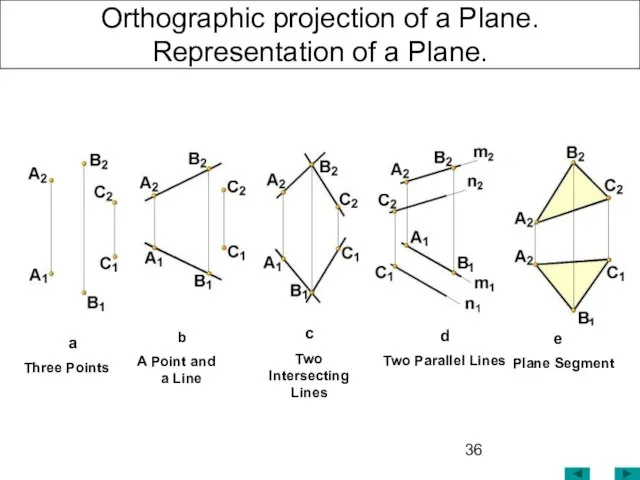
- 36. Orthographic projection of a Plane. Representation of a Plane. b A Point and a Line a
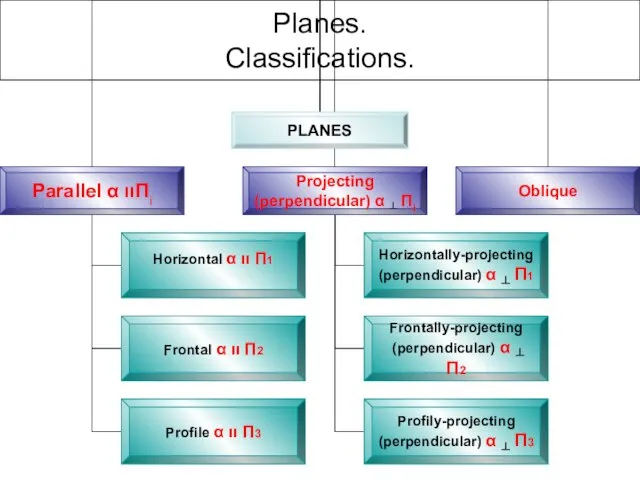
- 37. Planes. Classifications.
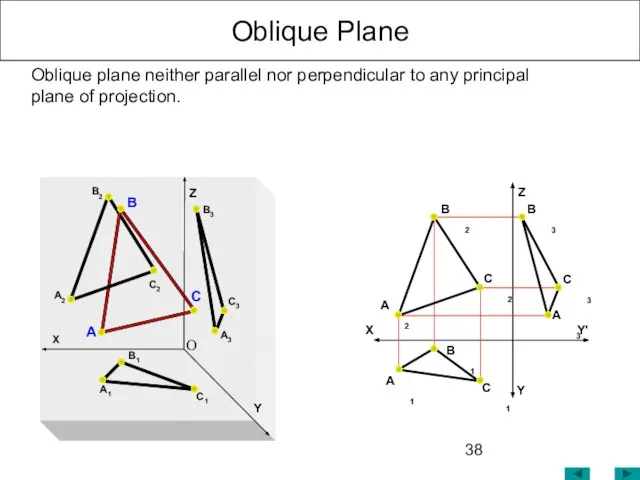
- 38. Oblique Plane Z Y' Y X Oblique plane neither parallel nor perpendicular to any principal plane
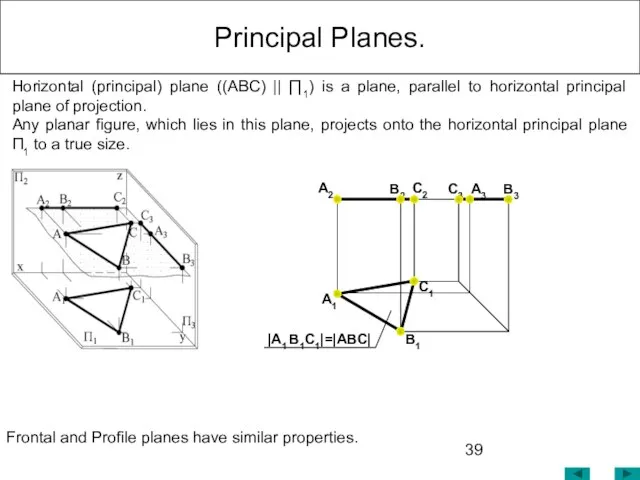
- 39. Principal Planes. Horizontal (principal) plane ((ABC) || ∏1) is a plane, parallel to horizontal principal plane
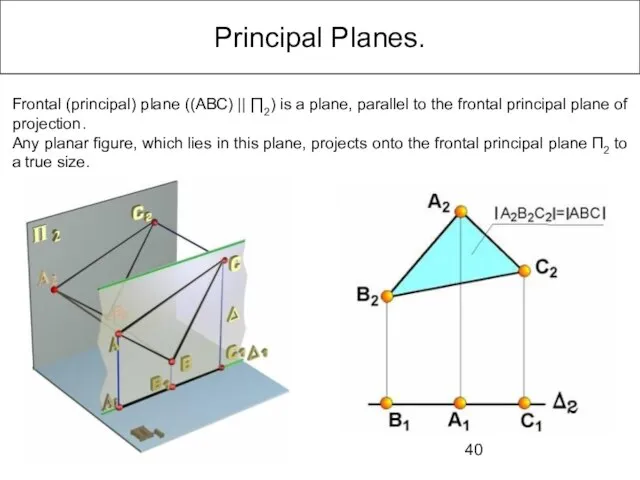
- 40. Principal Planes. Frontal (principal) plane ((ABC) || ∏2) is a plane, parallel to the frontal principal
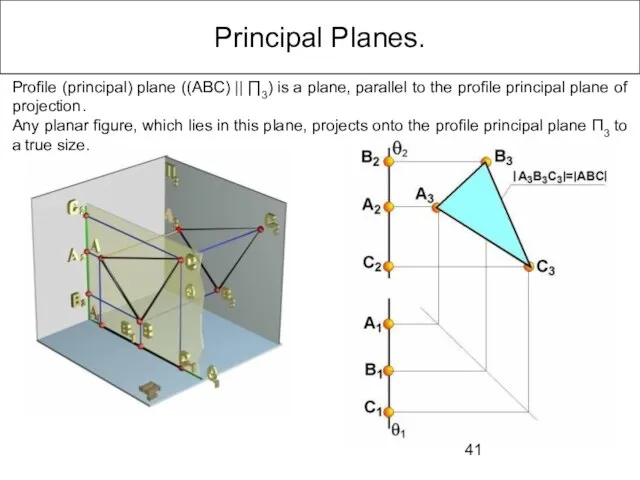
- 41. Principal Planes. Profile (principal) plane ((ABC) || ∏3) is a plane, parallel to the profile principal
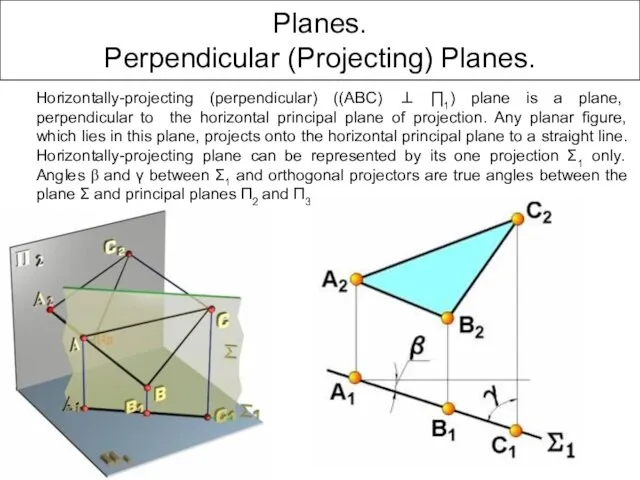
- 42. Planes. Perpendicular (Projecting) Planes. Horizontally-projecting (perpendicular) ((ABC) ⊥ ∏1) plane is a plane, perpendicular to the
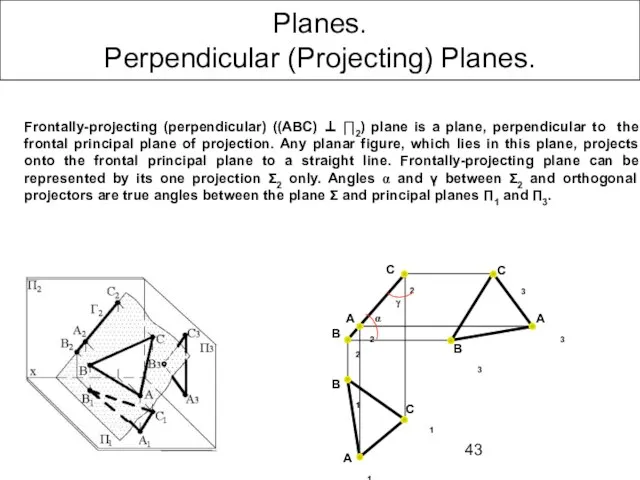
- 43. Planes. Perpendicular (Projecting) Planes. Frontally-projecting (perpendicular) ((ABC) ⊥ ∏2) plane is a plane, perpendicular to the
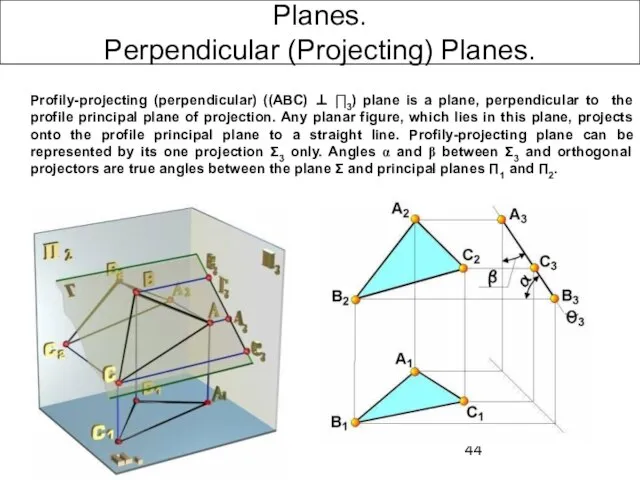
- 44. Planes. Perpendicular (Projecting) Planes. Profily-projecting (perpendicular) ((ABC) ⊥ ∏3) plane is a plane, perpendicular to the
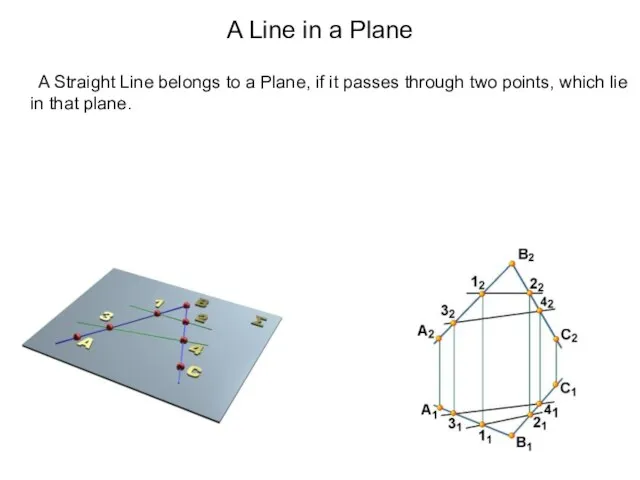
- 45. A Line in a Plane A Straight Line belongs to a Plane, if it passes through
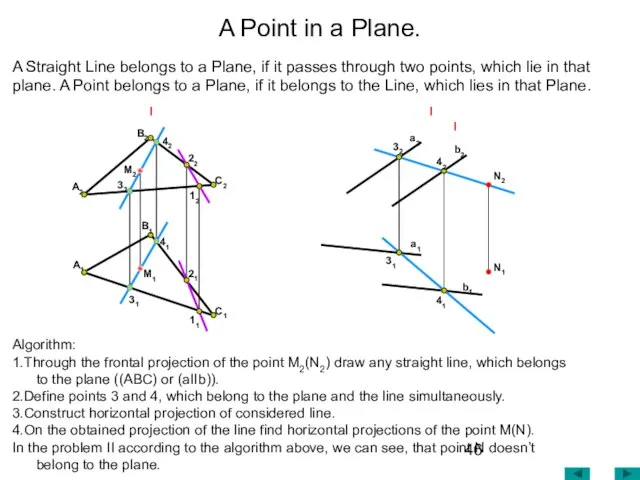
- 46. A Point in a Plane. Algorithm: 1.Through the frontal projection of the point М2(N2) draw any
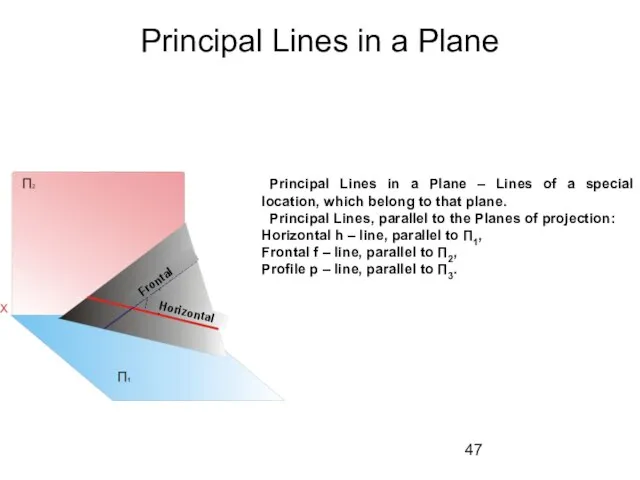
- 47. Principal Lines in a Plane Principal Lines in a Plane – Lines of a special location,
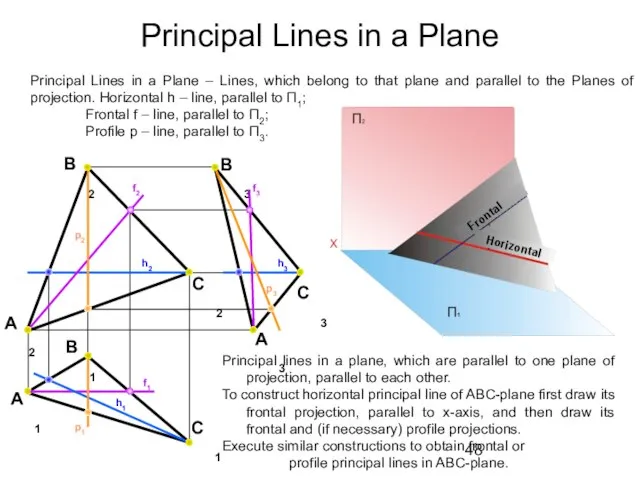
- 48. Principal Lines in a Plane B2 A2 C2 B3 A3 C1 B1 A1 Principal lines in
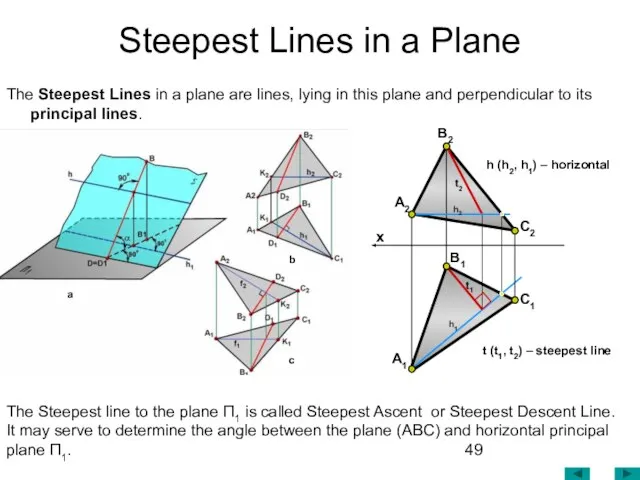
- 49. Steepest Lines in a Plane The Steepest Lines in a plane are lines, lying in this
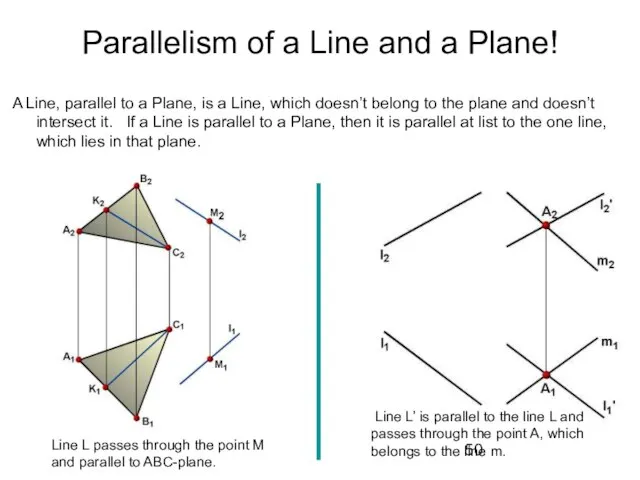
- 50. Parallelism of a Line and a Plane! A Line, parallel to a Plane, is a Line,
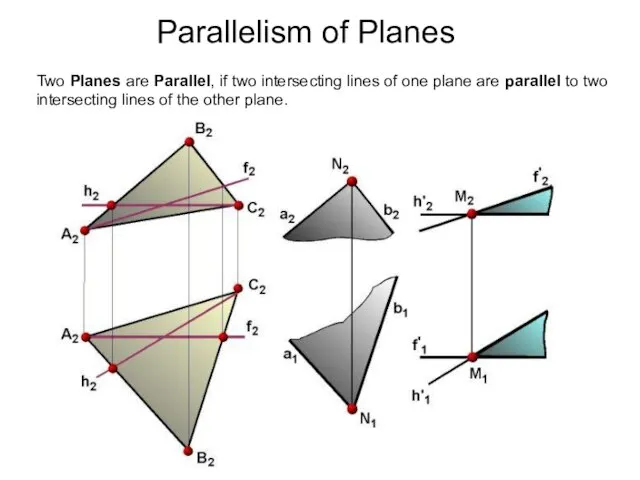
- 51. Two Planes are Parallel, if two intersecting lines of one plane are parallel to two intersecting
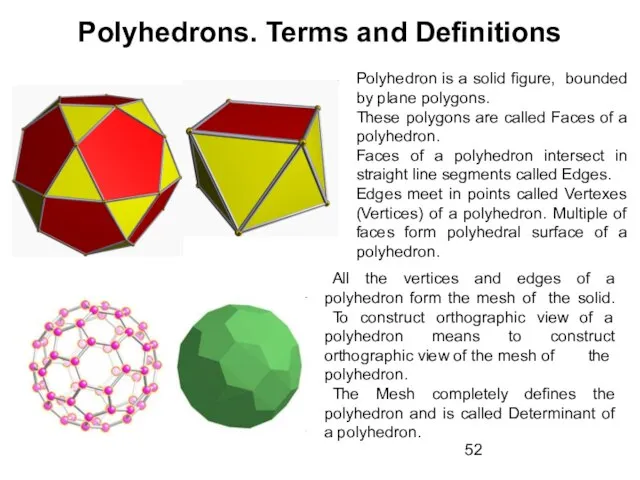
- 52. Polyhedrons. Terms and Definitions Polyhedron is a solid figure, bounded by plane polygons. These polygons are
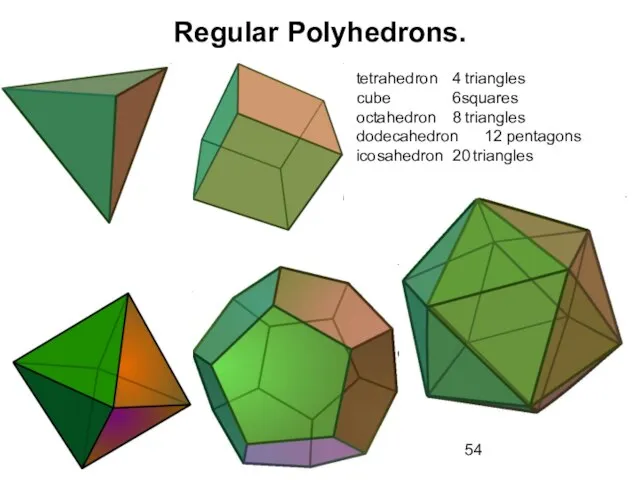
- 53. Regular Polyhedrons. A Regular polyhedron is a polyhedron whose faces are all regular polygons which are
- 54. Regular Polyhedrons. tetrahedron 4 triangles cube 6squares octahedron 8 triangles dodecahedron 12 pentagons icosahedron 20 triangles
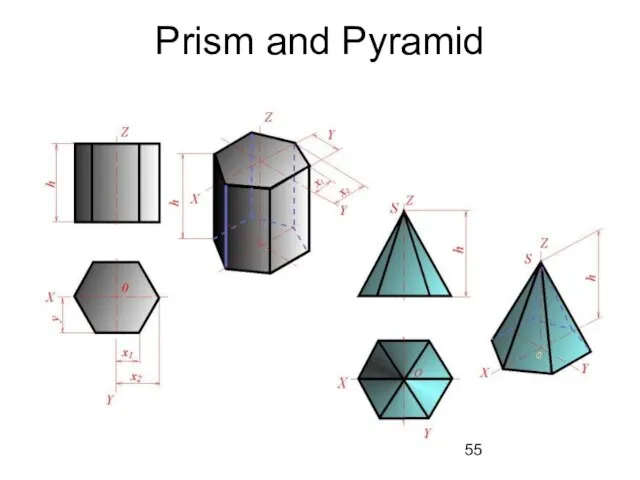
- 55. Prism and Pyramid
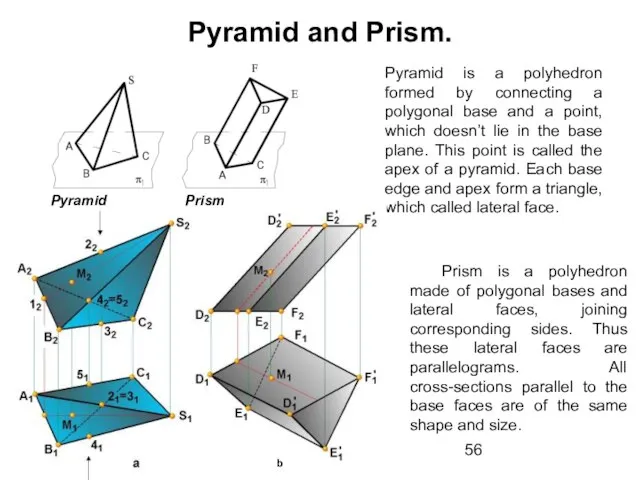
- 56. Pyramid and Prism. Pyramid is a polyhedron formed by connecting a polygonal base and a point,
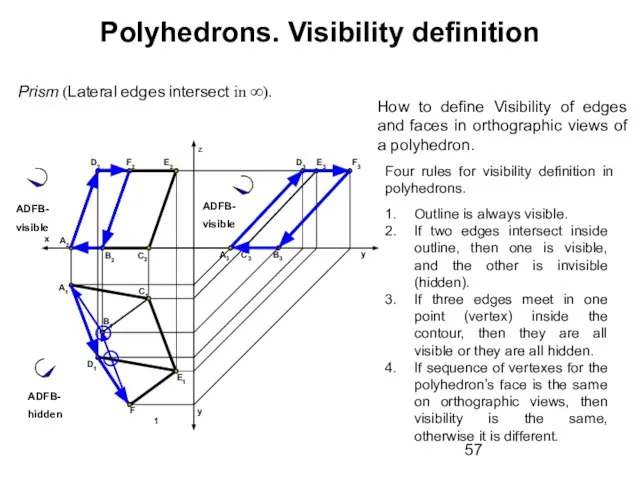
- 57. Polyhedrons. Visibility definition Prism (Lateral edges intersect in ∞). A1 D1 C2 C1 y y z
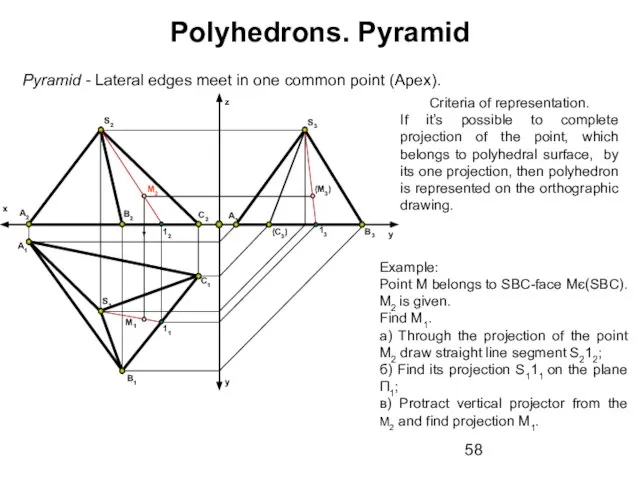
- 58. Polyhedrons. Pyramid Pyramid - Lateral edges meet in one common point (Apex). B1 y A2 A1
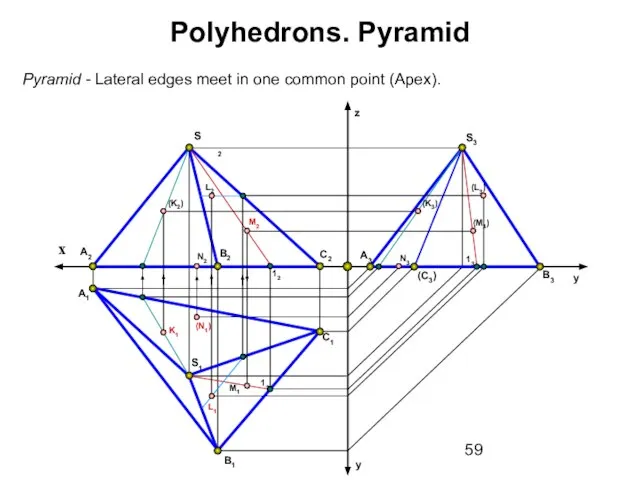
- 59. B1 y A2 A1 x B2 C1 C2 y z S2 S1 Pyramid - Lateral edges
- 61. Скачать презентацию




 Лекарственная терапия и продолжительность жизни: желаемое и действительное
Лекарственная терапия и продолжительность жизни: желаемое и действительное Яичница в корзиночках из бекона
Яичница в корзиночках из бекона THE DATA OF MACROECONOMICS
THE DATA OF MACROECONOMICS Викторина Я выбираю спорт
Викторина Я выбираю спорт Концепт беспилотного автомобиля
Концепт беспилотного автомобиля Планируемые результаты освоения обучающимися основной образовательной программы НОО
Планируемые результаты освоения обучающимися основной образовательной программы НОО Законодательство в области вакцинопрофилактики
Законодательство в области вакцинопрофилактики Политическая система общества
Политическая система общества Особенности контрактов со спортсменом и тренером. Лекция 10
Особенности контрактов со спортсменом и тренером. Лекция 10 Расходы организаций
Расходы организаций Власова Валентина Ивановна Образование: высшее, РГПИ, 1984г. Специальность: учитель начальных классов Стаж работы: 33 года, в
Власова Валентина Ивановна Образование: высшее, РГПИ, 1984г. Специальность: учитель начальных классов Стаж работы: 33 года, в  В рамках реализации Федеральной целевой программы «Патриотическое воспитание граждан Российской Федерации, увековечение памяти
В рамках реализации Федеральной целевой программы «Патриотическое воспитание граждан Российской Федерации, увековечение памяти  Радиоэлектронная борьба
Радиоэлектронная борьба Что такое зоопарк? 1 класс
Что такое зоопарк? 1 класс Система дарения напитков онлайн Презентация для инвестора
Система дарения напитков онлайн Презентация для инвестора Обряды и традиции казаков
Обряды и традиции казаков Альфа-, бета- и гамма излучения. Радиоактивные превращения
Альфа-, бета- и гамма излучения. Радиоактивные превращения Экономическая эффективность и основные направления интенсификации молочного скотоводства в ОАО Красная Буда
Экономическая эффективность и основные направления интенсификации молочного скотоводства в ОАО Красная Буда Интерактивная доска нового поколения PolyVision eno flex как средство развития педагогического мастерства
Интерактивная доска нового поколения PolyVision eno flex как средство развития педагогического мастерства Автоматизированная система управления наружным освещением (АСУНО)
Автоматизированная система управления наружным освещением (АСУНО) Правоохранительные органы
Правоохранительные органы Игры дедушек и бабушек
Игры дедушек и бабушек Фестиваль В гостях у Воеводы
Фестиваль В гостях у Воеводы Презентация на тему Этнический и религиозный состав населения
Презентация на тему Этнический и религиозный состав населения СОВЕТСКИЙ ТЫЛ В ВЕЛИКОЙ ОТЕЧЕСТВЕННОЙ ВОЙНЕ 1941-1945гг.
СОВЕТСКИЙ ТЫЛ В ВЕЛИКОЙ ОТЕЧЕСТВЕННОЙ ВОЙНЕ 1941-1945гг.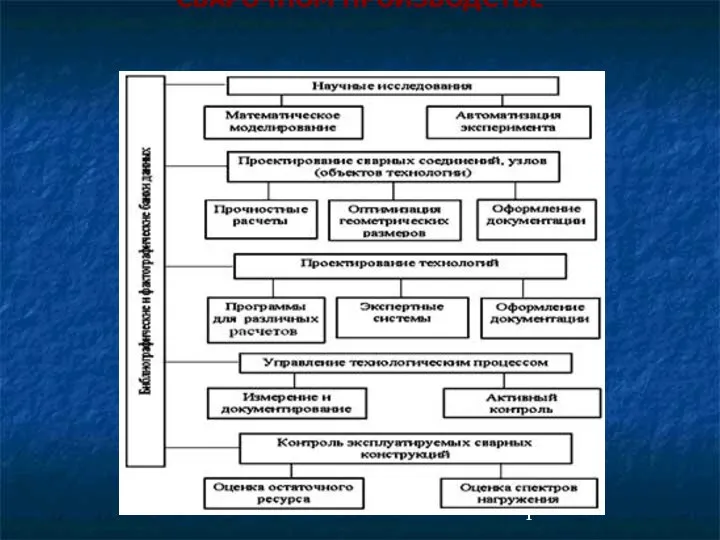 Современные наукоемкие технологии в сварочном производстве
Современные наукоемкие технологии в сварочном производстве Из серии " 100 великих картин "
Из серии " 100 великих картин " Деньги и ценные бумаги
Деньги и ценные бумаги