Содержание
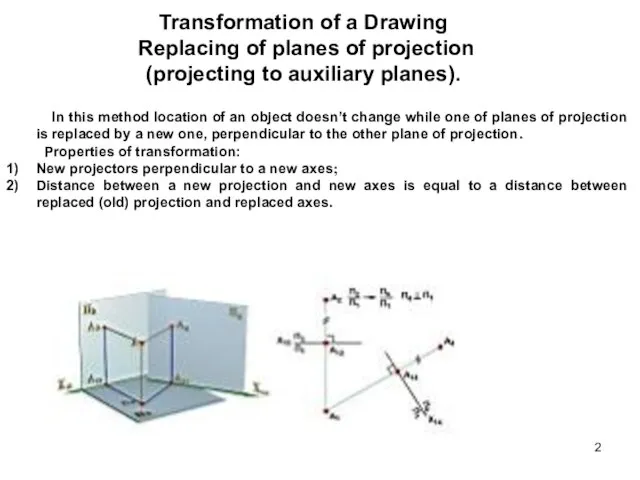
- 2. Transformation of a Drawing Replacing of planes of projection (projecting to auxiliary planes). In this method
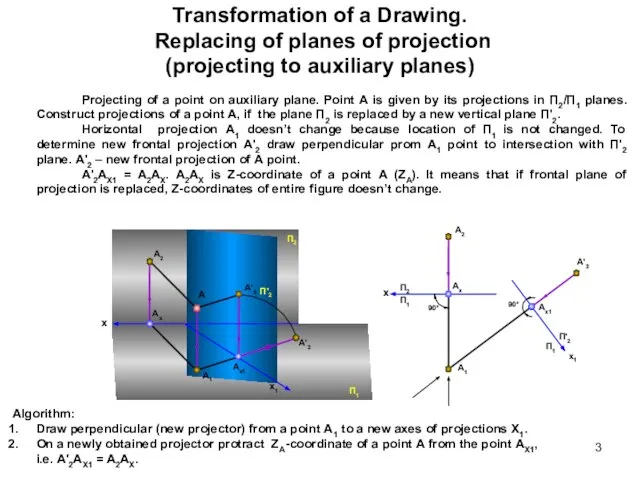
- 3. Transformation of a Drawing. Replacing of planes of projection (projecting to auxiliary planes) Projecting of a
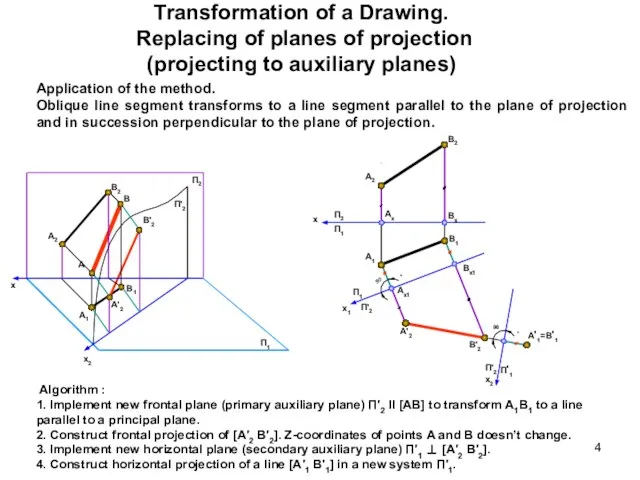
- 4. Transformation of a Drawing. Replacing of planes of projection (projecting to auxiliary planes) Application of the
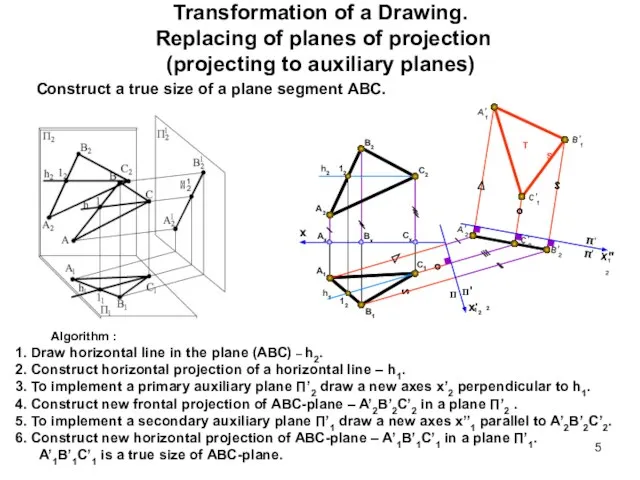
- 5. Transformation of a Drawing. Replacing of planes of projection (projecting to auxiliary planes) Construct a true
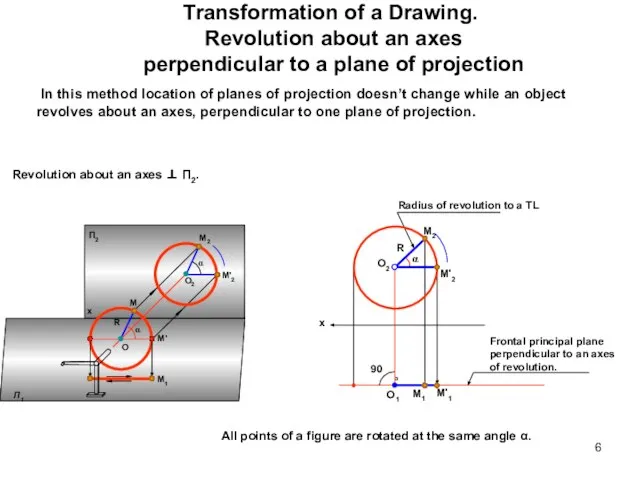
- 6. Transformation of a Drawing. Revolution about an axes perpendicular to a plane of projection In this
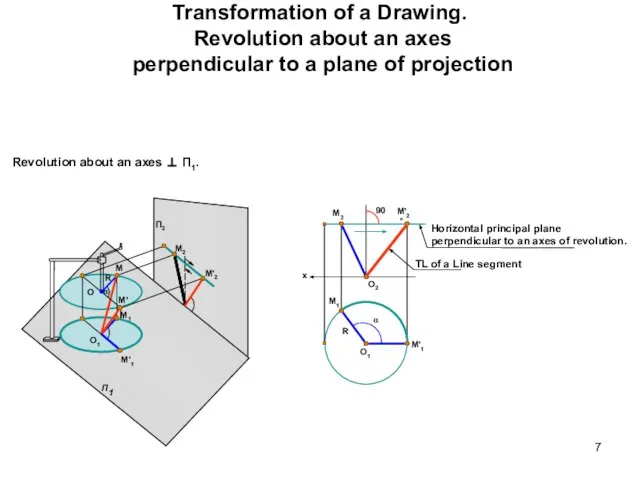
- 7. Transformation of a Drawing. Revolution about an axes perpendicular to a plane of projection Revolution about
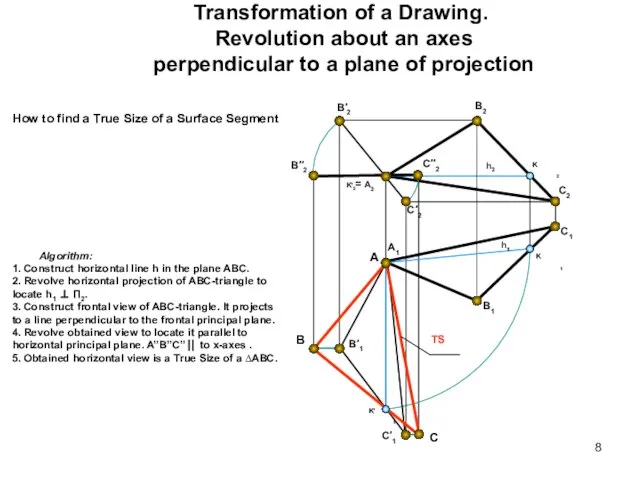
- 8. Transformation of a Drawing. Revolution about an axes perpendicular to a plane of projection B2 A2
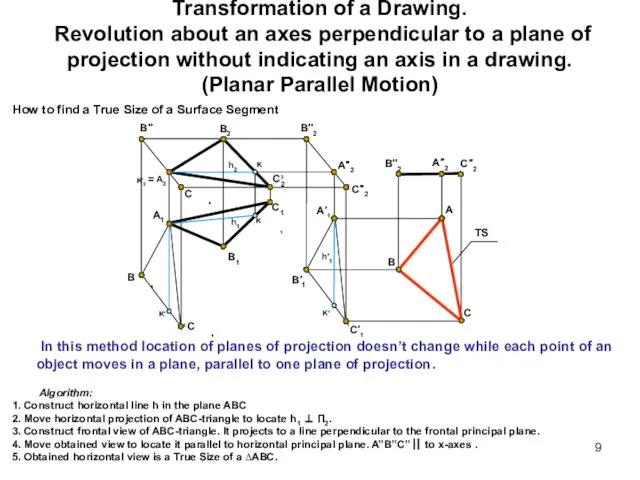
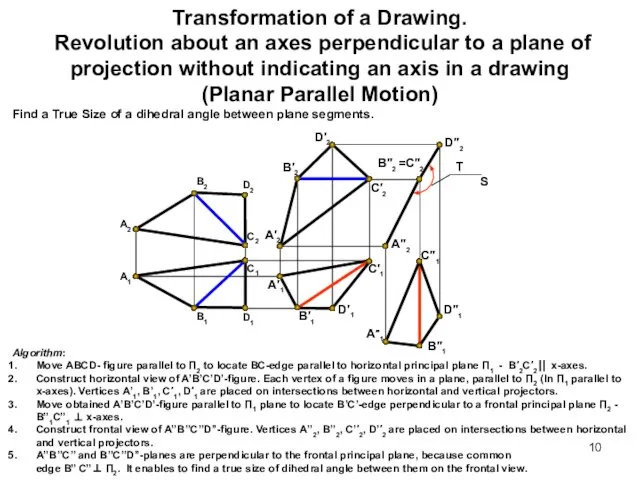
- 9. Transformation of a Drawing. Revolution about an axes perpendicular to a plane of projection without indicating
- 10. Transformation of a Drawing. Revolution about an axes perpendicular to a plane of projection without indicating
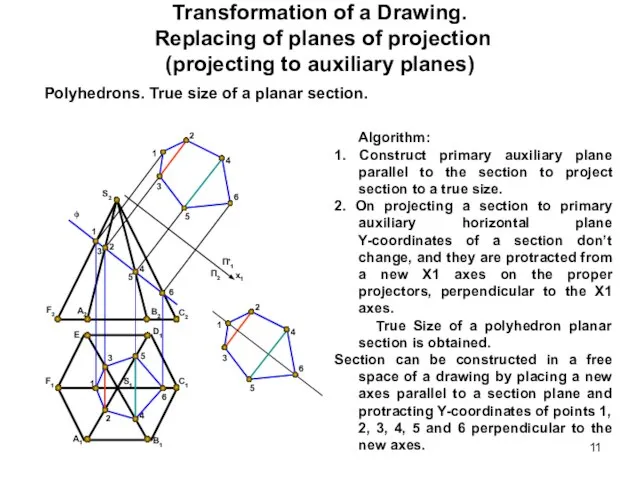
- 11. Transformation of a Drawing. Replacing of planes of projection (projecting to auxiliary planes) Polyhedrons. True size
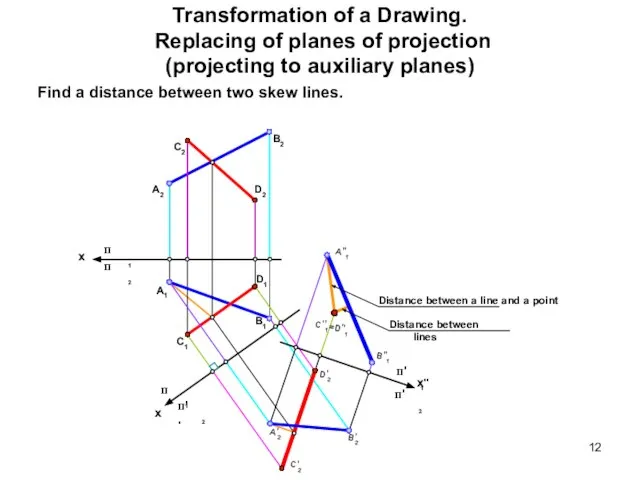
- 12. Transformation of a Drawing. Replacing of planes of projection (projecting to auxiliary planes) Find a distance
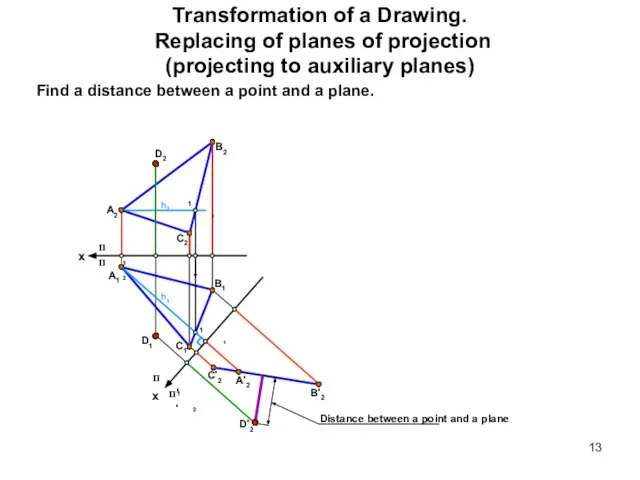
- 13. Transformation of a Drawing. Replacing of planes of projection (projecting to auxiliary planes) Find a distance
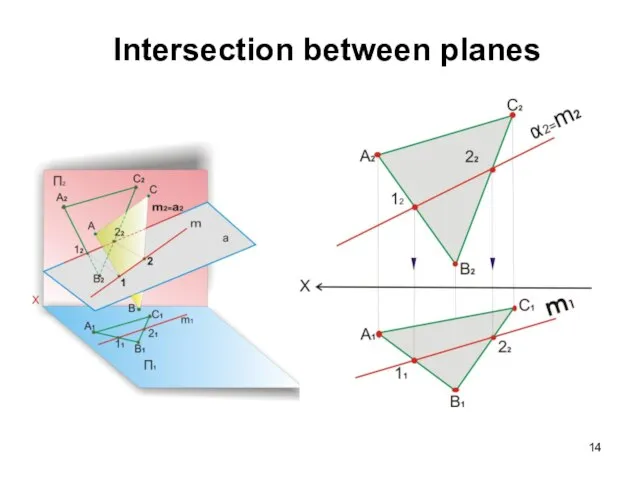
- 14. Intersection between planes
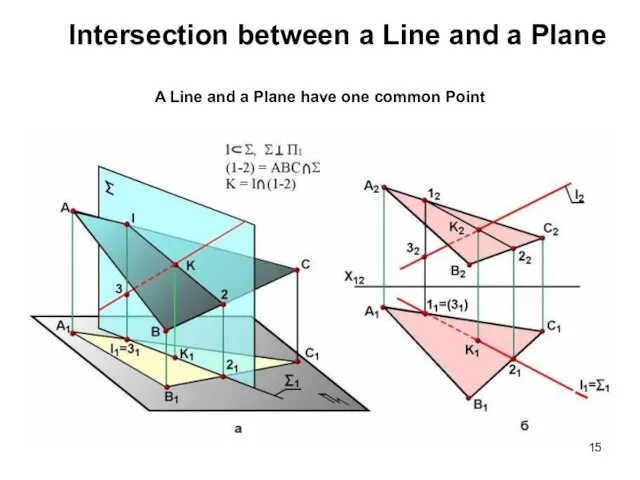
- 15. Intersection between a Line and a Plane A Line and a Plane have one common Point
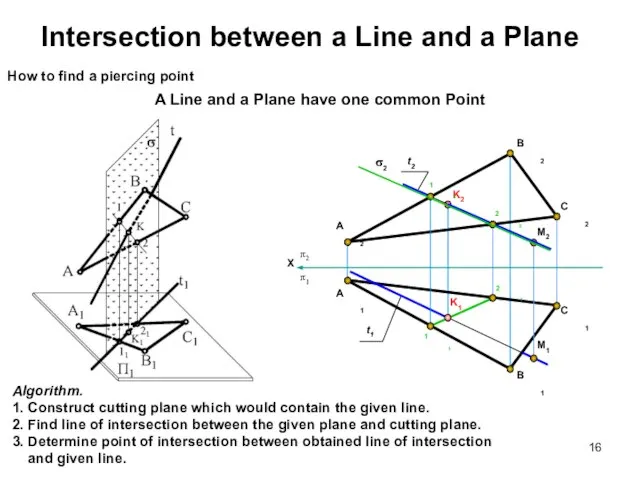
- 16. Intersection between a Line and a Plane A Line and a Plane have one common Point
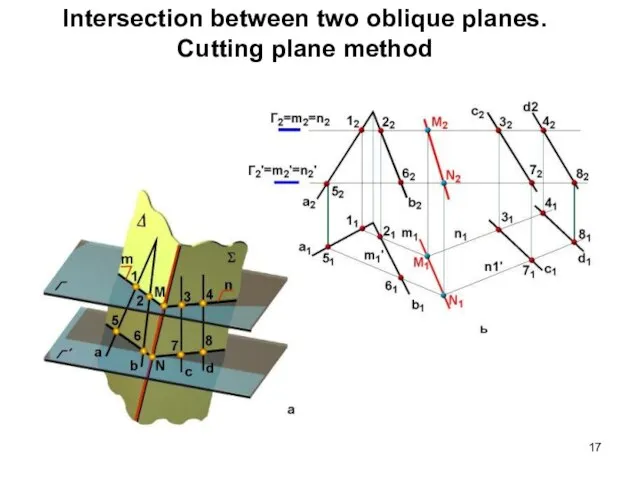
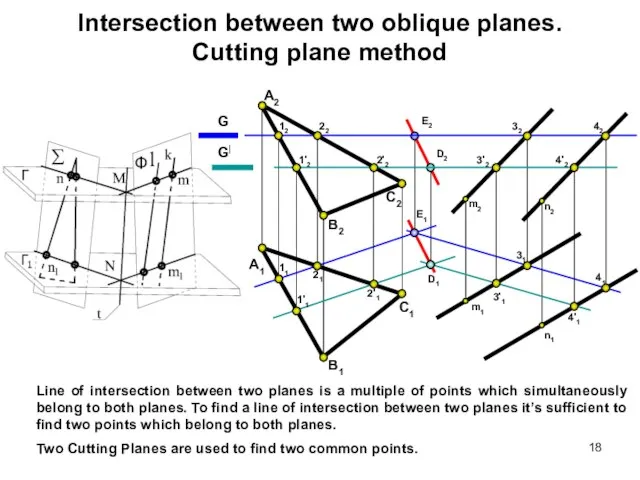
- 17. Intersection between two oblique planes. Cutting plane method
- 18. Intersection between two oblique planes. Cutting plane method Line of intersection between two planes is a
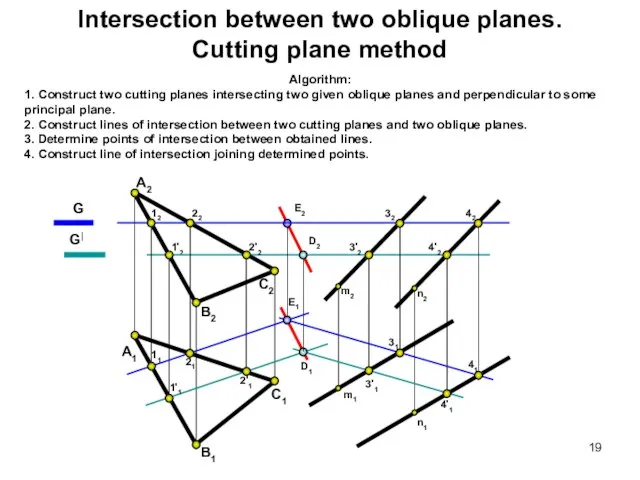
- 19. Intersection between two oblique planes. Cutting plane method Algorithm: 1. Construct two cutting planes intersecting two
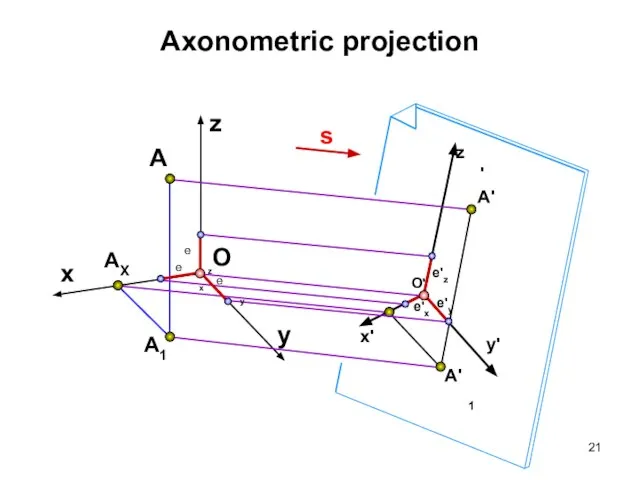
- 20. Axonometric projection The word 'axonometry' (Greek) consists of two words: 'axon'—axis and 'metreo'—I measure, and means
- 21. Axonometric projection A1 x AX A O z y
- 22. Axonometric projection A line segment e is laid off on the axes x, y, z, and
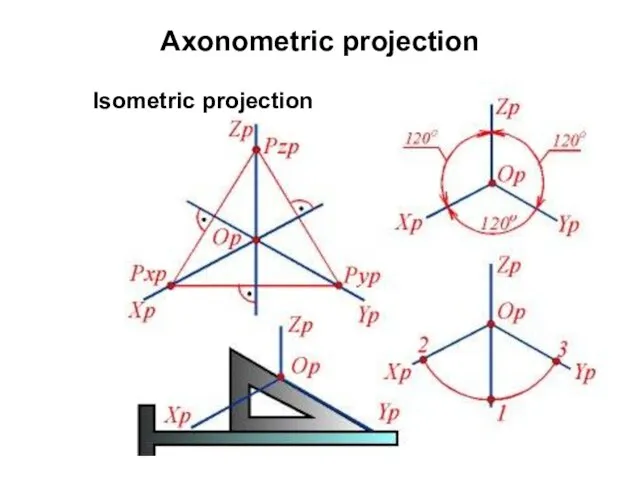
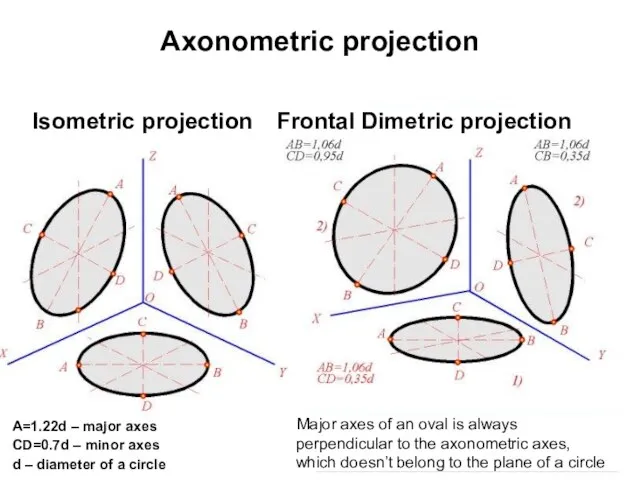
- 23. Axonometric projection Isometric projection
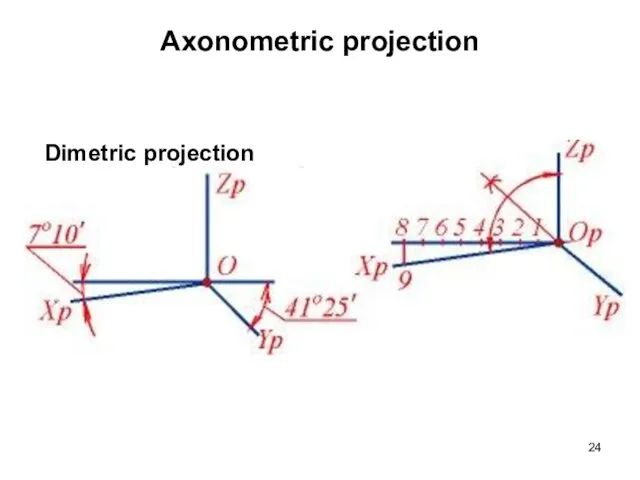
- 24. Axonometric projection Dimetric projection
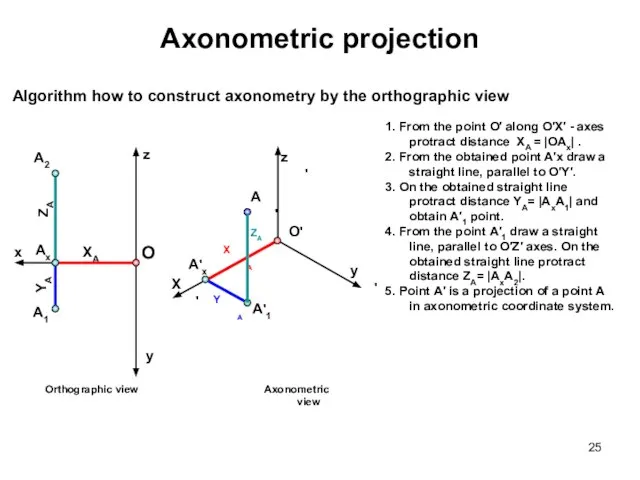
- 25. 1. From the point О′ along О′Х′ - axes protract distance XA = |ОAx| . 2.
- 26. Axonometric projection Isometric projection Frontal Dimetric projection A=1.22d – major axes CD=0.7d – minor axes d
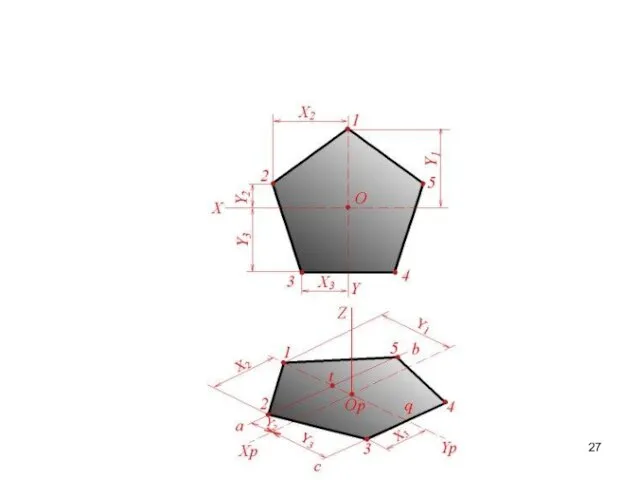
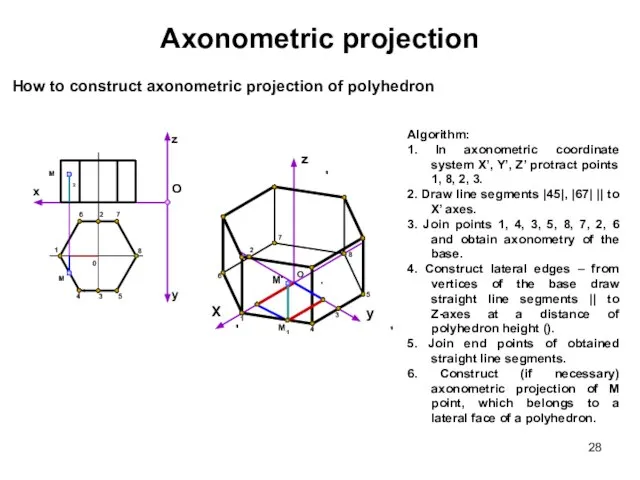
- 28. Axonometric projection Algorithm: 1. In axonometric coordinate system X’, Y’, Z’ protract points 1, 8, 2,
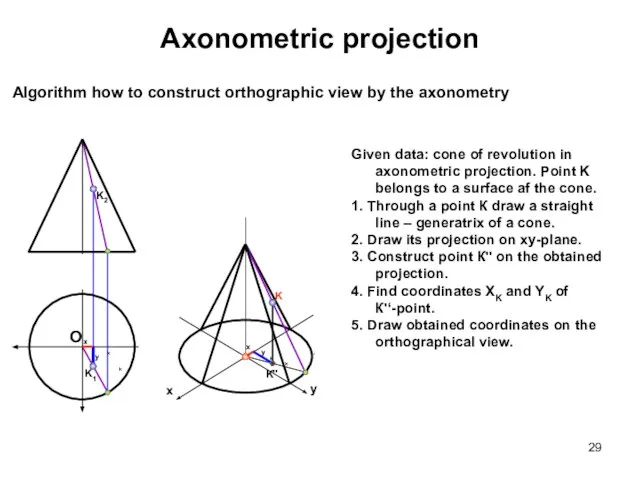
- 29. Axonometric projection Algorithm how to construct orthographic view by the axonometry Given data: cone of revolution
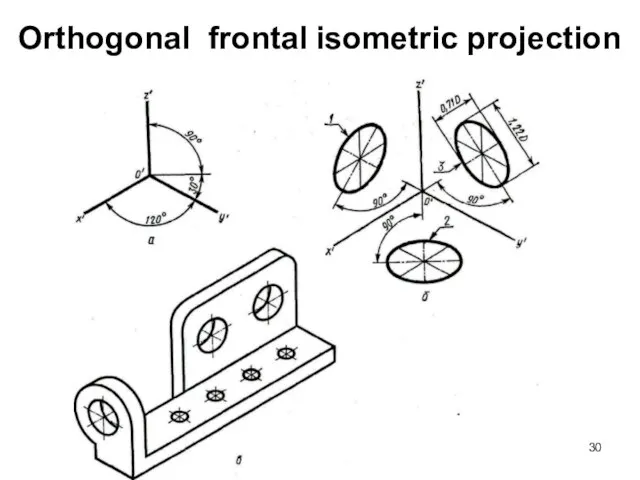
- 30. Orthogonal frontal isometric projection
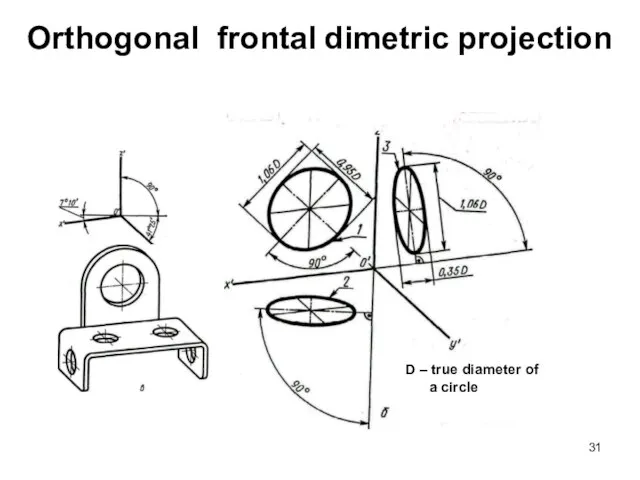
- 31. Orthogonal frontal dimetric projection D – true diameter of a circle
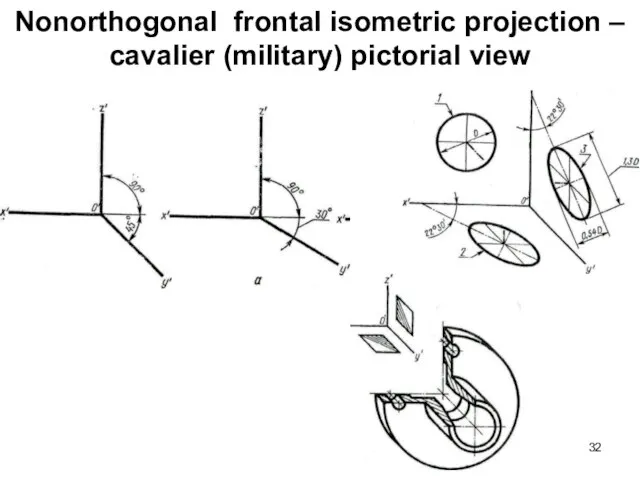
- 32. Nonorthogonal frontal isometric projection – cavalier (military) pictorial view
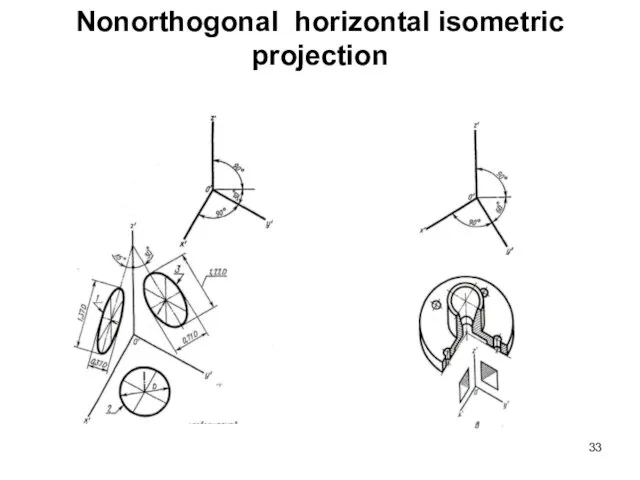
- 33. Nonorthogonal horizontal isometric projection
- 35. Скачать презентацию


 ilin
ilin Проект по созданию брошюры Я в мире прав (1)
Проект по созданию брошюры Я в мире прав (1) Презентация на тему Знаки зодиака
Презентация на тему Знаки зодиака  Особенности маркетинга материально-технических средств. Лекция № 4.1
Особенности маркетинга материально-технических средств. Лекция № 4.1 Изменение энергии системы U происходит при совершении над ней работы каждой из сил Xi: (3.1)
Изменение энергии системы U происходит при совершении над ней работы каждой из сил Xi: (3.1) 20170426_prezentatsiya_simbirskiy_kray_1_chast
20170426_prezentatsiya_simbirskiy_kray_1_chast Древние образы и символы в народном искусстве.Часть 1
Древние образы и символы в народном искусстве.Часть 1 Обучение в ИФНиТ
Обучение в ИФНиТ 3. Годовой производственно-финансовый план деятельности СЕЛЬСКОХОЗЯЙСТВЕННОГО ПРЕДПРИЯТИЯ
3. Годовой производственно-финансовый план деятельности СЕЛЬСКОХОЗЯЙСТВЕННОГО ПРЕДПРИЯТИЯ ОБЩЕСТВЕННОЕ УЧАСТИЕ В УПРАВЛЕНИИ ШКОЛОЙ: ПУТЬ К ИЗМЕНЕНИЮ ОБРАЗОВАТЕЛЬНОЙ ПОЛИТИКИ ШКОЛЫ
ОБЩЕСТВЕННОЕ УЧАСТИЕ В УПРАВЛЕНИИ ШКОЛОЙ: ПУТЬ К ИЗМЕНЕНИЮ ОБРАЗОВАТЕЛЬНОЙ ПОЛИТИКИ ШКОЛЫ Промышленный скетч
Промышленный скетч Регулирующий подход к государственным и частным компаниям
Регулирующий подход к государственным и частным компаниям Вклад Федерального казначейства в создание и развитие Информационного Общества
Вклад Федерального казначейства в создание и развитие Информационного Общества Shkolnik_prevraschaetsya_v_benzopilu_i_delaet_vsyakoe
Shkolnik_prevraschaetsya_v_benzopilu_i_delaet_vsyakoe АИМ_шрифт_элементы_цвета Брендбук
АИМ_шрифт_элементы_цвета Брендбук СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ И ИНФОРМАЦИОННАЯ ПОДДЕРЖКА МНОГОПРОДУКТОВЫХ ПРОИЗВОДИТЕЛЬНЫХ СИСТЕМЛЕСНОГО КОМПЛЕКСА
СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ И ИНФОРМАЦИОННАЯ ПОДДЕРЖКА МНОГОПРОДУКТОВЫХ ПРОИЗВОДИТЕЛЬНЫХ СИСТЕМЛЕСНОГО КОМПЛЕКСА Интелектуальная игра
Интелектуальная игра 20 начина да си затриeте блога, без да се усетите
20 начина да си затриeте блога, без да се усетите Растительные наркотики.
Растительные наркотики. Електричне поле. Закон Кулона
Електричне поле. Закон Кулона Я выбираю жизнь
Я выбираю жизнь Викторина по роману в стихах А. С. Пушкина «ЕВГЕНИЙ ОНЕГИН»
Викторина по роману в стихах А. С. Пушкина «ЕВГЕНИЙ ОНЕГИН» История о философском камне
История о философском камне Презентация на тему Действительные причастия настоящего времени (7 класс)
Презентация на тему Действительные причастия настоящего времени (7 класс) Определение потребности работодателей в привлечении трудящихся-мигрантов Михаил Крощенко НИИ труда и социального страховани
Определение потребности работодателей в привлечении трудящихся-мигрантов Михаил Крощенко НИИ труда и социального страховани Problems of international logistics
Problems of international logistics Организация работы кондитерского цеха
Организация работы кондитерского цеха Возникновение и начальное развитие жизни на Земле
Возникновение и начальное развитие жизни на Земле