Содержание
- 4. Натуральные числа Числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий»...),
- 5. Действия с натуральными числами + * - / При сложении и умножении натуральных чисел результатом всегда
- 6. Целые числа Числа из множества {0, 1, -1, 2, -2, ....}, называют целыми. Это множество состоит
- 7. Действия с целыми числами + * - / Целые числа Результат может не быть целым числом
- 8. Рациональные числа
- 9. Действия с рациональными числами + * - / Рациональные числа
- 10. Множества чисел R Q Z N
- 11. Десятичные дроби где m- целое число k- натуральное число Можно записать в виде конечное десятичной дроби
- 12. Периодическая дробь бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та
- 13. Алгоритм перевода периодической дроби в обычную Вариант 1 Вариант 2 Если после запятой сразу следует период
- 15. Скачать презентацию












 (–1) · 3 =
(–1) · 3 = Осмотр общего имущества в многоквартирном доме
Осмотр общего имущества в многоквартирном доме EV3 Самосвал
EV3 Самосвал Инвестиционный фонд МАП «Инновационный лифт»
Инвестиционный фонд МАП «Инновационный лифт» Нам нужны союзники!
Нам нужны союзники! Дисциплина: Международные перевозки грузов РАЗДЕЛ 3. Обеспечивающий комплекс организации международной перевозки грузов Тема 3
Дисциплина: Международные перевозки грузов РАЗДЕЛ 3. Обеспечивающий комплекс организации международной перевозки грузов Тема 3 Мое зазеркалье
Мое зазеркалье Московский колледж бизнес-технологий. Эксплуатация беспилотных авиационных систем
Московский колледж бизнес-технологий. Эксплуатация беспилотных авиационных систем Презентация Microsoft PowerPoint (3)
Презентация Microsoft PowerPoint (3) Презентация на тему Иудаизм презентация 4 класс
Презентация на тему Иудаизм презентация 4 класс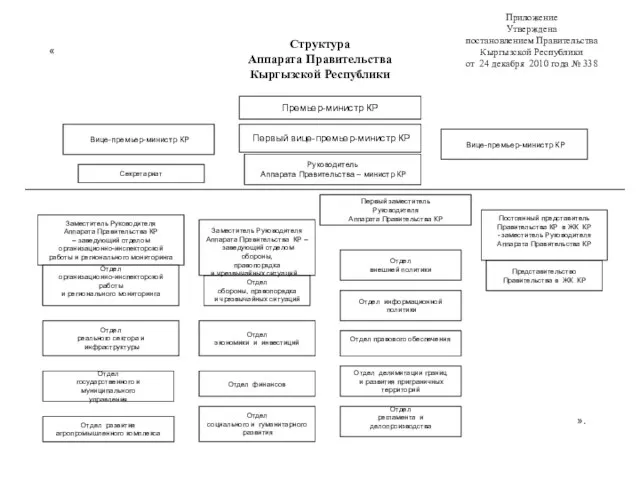 Структура Аппарата Правительства Кыргызской Республики
Структура Аппарата Правительства Кыргызской Республики Автоматизированная информационная система «Государственный заказ»
Автоматизированная информационная система «Государственный заказ» Формирование экологической культуры обучающихся колледжа через реализацию социально-образовательых проектов
Формирование экологической культуры обучающихся колледжа через реализацию социально-образовательых проектов Тема урока «Право на труд. Трудовые правоотношения»
Тема урока «Право на труд. Трудовые правоотношения» Класс 1-1 3주 후 시험문제 읽기 Чтение
Класс 1-1 3주 후 시험문제 읽기 Чтение Обобщающий урок - игра по теме: «Я знаю край родной».
Обобщающий урок - игра по теме: «Я знаю край родной». Тяжелая атлетика в России и за рубежом
Тяжелая атлетика в России и за рубежом Разработка мероприятия Цифровой текстиль. Синтетические ткани
Разработка мероприятия Цифровой текстиль. Синтетические ткани Лекция_6 ЭТД ФТД.ppt
Лекция_6 ЭТД ФТД.ppt Презентация на тему Сочинение по картине Левитана «Весна. Большая вода» 4 класс
Презентация на тему Сочинение по картине Левитана «Весна. Большая вода» 4 класс Методы мониторинга репутациив социальных медиа
Методы мониторинга репутациив социальных медиа Областной конкурспервичных профсоюзныхорганизаций.
Областной конкурспервичных профсоюзныхорганизаций. Контроль квалификации сварщиков. Система аттестации сварочного производства
Контроль квалификации сварщиков. Система аттестации сварочного производства Уголовное законодательство Республики Казахстан на страже воинского правопорядка (занятие 1)
Уголовное законодательство Республики Казахстан на страже воинского правопорядка (занятие 1) 36736
36736 Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс)
Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс) Электрическая лампа накаливания
Электрическая лампа накаливания 20161206_avstraliya-i-okeaniya
20161206_avstraliya-i-okeaniya