Содержание
- 2. Логарифмічними рівняннями називаються рівняння, які містять змінну під знаком логарифма Які із даних рівняннь є логарифмічними?
- 3. Розв’язати логарифмічне рівняння – це означає знайти всі його корені або довести, що рівняння коренів не
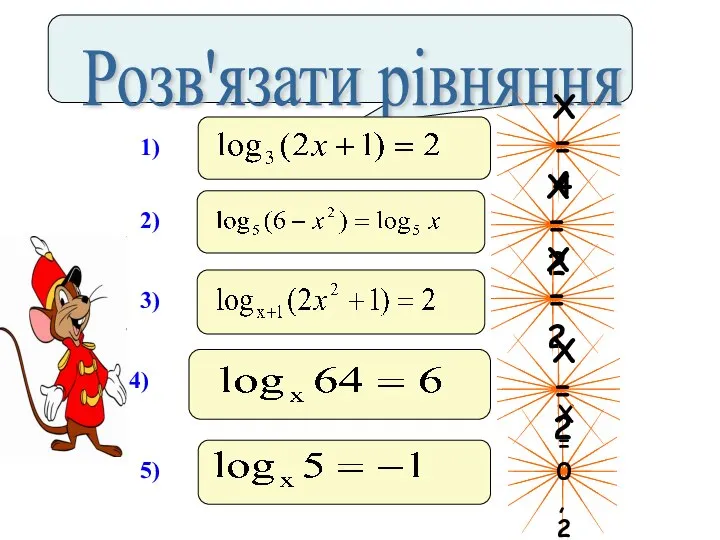
- 4. Розв'язати рівняння Х=4 Х=2 Х=2 Х=0,2 Х=2
- 5. Існують основні методи розв’язування логарифмічних рівнянь: Метод введення нової змінної; Метод потенціювання; Метод логарифмування; Метод пильного
- 6. Розв'язати рівняння
- 7. Метод зведення логарифмічного рівняння до алгебраїчного Приклад: Розв'яжіть рівняння Метод потенціювання. Приклад: Розв'яжіть рівняння Пропотенціюємо дану
- 8. Метод зведення логарифмів до однієї і тієї ж основи. Приклад: Розв'яжіть рівняння Метод логарифмування Приклад: Розв'яжіть
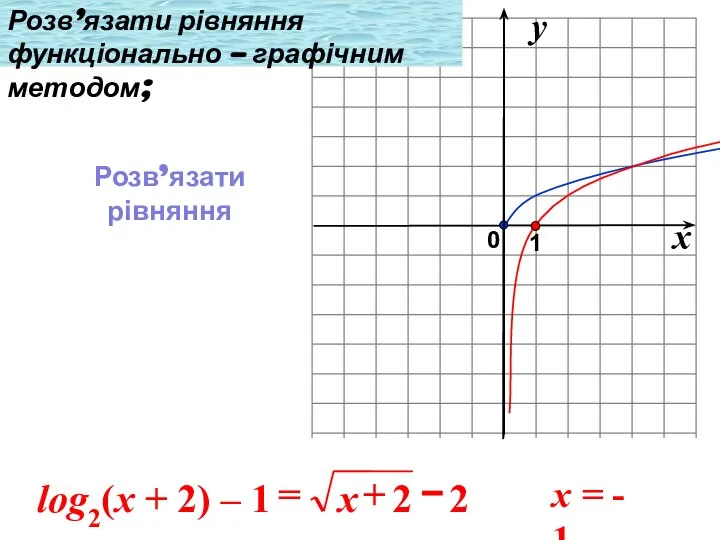
- 9. x = - 1 Розв’язати рівняння функціонально – графічним методом; Розв’язати рівняння
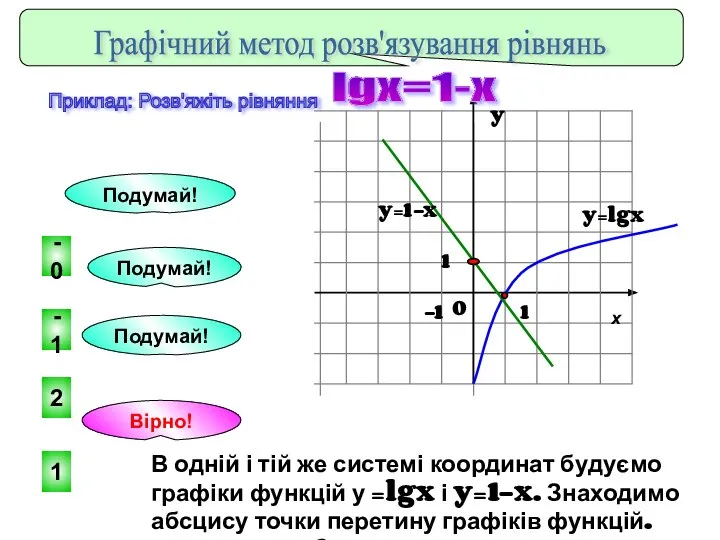
- 10. . 1 -1 2 -0 Подумай! Подумай! Вірно! Подумай! x Графічний метод розв'язування рівнянь y=lgx y=1-x
- 11. Іраціональні логарифмічні рівняння: Враховуючи ОДЗ, дане рівняння рівносильне системі: Відповідь: 32,75 Розв’язування : Розв’язати рівняння:
- 12. Іраціональні логарифмічні рівняння: Враховуючи ОДЗ, дане рівняння рівносильне системі: Відповідь: 32,75 Розв’язування : Розв’язати рівняння:
- 13. Логарифмічні рівняння, що містять модуль Приклад: Розв'яжіть рівняння Приклад: Розв'яжіть рівняння О.Д.З. х Відповідь: не має
- 14. Розв'язування показникових логарифмічних рівняння: Відповідь: Розв’язування : Розв’язати нерівність:
- 16. Скачать презентацию










 Комплекс качеств и свойств в формировании имиджа фирмы
Комплекс качеств и свойств в формировании имиджа фирмы Защита интеллектуальной собственности
Защита интеллектуальной собственности Гражданство РФ
Гражданство РФ ИОМ
ИОМ ЭЛЕКТИВНЫЙ КУРС
ЭЛЕКТИВНЫЙ КУРС JV ANgel. Одежда (бренд)
JV ANgel. Одежда (бренд) Система финансового администрирования и контроля для территориально распределенных холдинговых структур
Система финансового администрирования и контроля для территориально распределенных холдинговых структур Длина окружности и площадь круга (9 класс)
Длина окружности и площадь круга (9 класс) Менеджмент в деятельности предприятия
Менеджмент в деятельности предприятия Оценка выбросов загрязняющих веществ в воздух от автотранспорта
Оценка выбросов загрязняющих веществ в воздух от автотранспорта Горячие напитки
Горячие напитки Летний оздоровительный лагерь Родничок
Летний оздоровительный лагерь Родничок Одно из свойств арифметических прогрессий
Одно из свойств арифметических прогрессий Обучающий курс по созданию бизнеса в сфере услуг
Обучающий курс по созданию бизнеса в сфере услуг Презентация на тему Развитие жизни в палеозойской эре Ранний палеозой (кембрий, ордовик, силур)
Презентация на тему Развитие жизни в палеозойской эре Ранний палеозой (кембрий, ордовик, силур)  Способы подъемов, спусков и торможения в лыжном спорте
Способы подъемов, спусков и торможения в лыжном спорте Маркетингове дослідження на українському авторинку та рекомендації для компанії Toyota
Маркетингове дослідження на українському авторинку та рекомендації для компанії Toyota Контрольные операции при фрезеровании
Контрольные операции при фрезеровании DLH_credentials_2022
DLH_credentials_2022 Продукты EduConsulting. Разработка интерактивных мультимедийных программ для детей дошкольного и младшего школьного возраста
Продукты EduConsulting. Разработка интерактивных мультимедийных программ для детей дошкольного и младшего школьного возраста Влагостойкое напольное покрытие. Коллекция AQUAFLOOR STONE
Влагостойкое напольное покрытие. Коллекция AQUAFLOOR STONE УСТАНОВКА УПАКОВОЧНАЯ ПОЛУАВТОМАТИЧЕСКАЯ
УСТАНОВКА УПАКОВОЧНАЯ ПОЛУАВТОМАТИЧЕСКАЯ НЕРВЫ НИЖНИХ КОНЕЧНОСТЕЙ
НЕРВЫ НИЖНИХ КОНЕЧНОСТЕЙ Личный товарооборот. Орифлейм
Личный товарооборот. Орифлейм Основные положения государственной политики обеспечения информационной безопасности Российской Федерации
Основные положения государственной политики обеспечения информационной безопасности Российской Федерации  Правовые основы сохранения и укрепления репродуктивного здоровья. Брак и семья
Правовые основы сохранения и укрепления репродуктивного здоровья. Брак и семья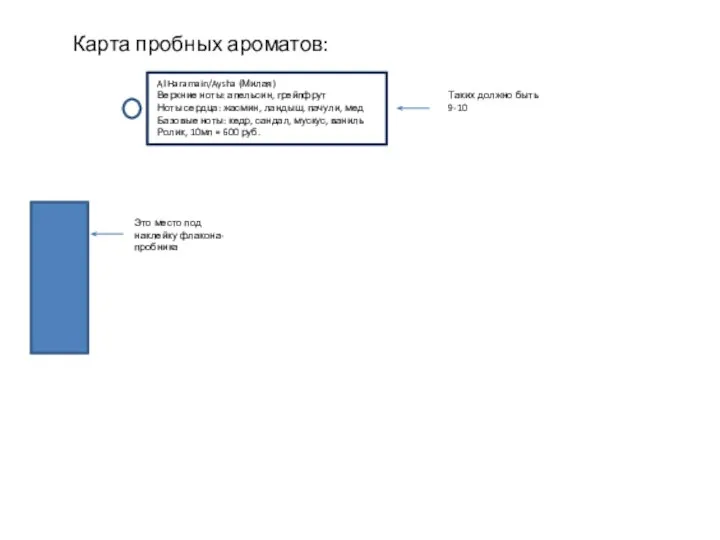 Карта пробных ароматов: Al Haramain/Aysha (милая)
Карта пробных ароматов: Al Haramain/Aysha (милая) Д.Н.Мамин – Сибиряк «Сказка про храброго Зайца, длинные уши, косые глаза, короткий хвост»
Д.Н.Мамин – Сибиряк «Сказка про храброго Зайца, длинные уши, косые глаза, короткий хвост»