Содержание
- 2. Искусство орнамента содержит в неявном виде наиболее древнюю часть известной нам высшей математике. Герман Вейль (известный
- 3. Орнамент – это узор, состоящий из ритмически упорядоченных элементов для украшения каких – либо предметов или
- 4. С другой стороны, при исследовании геометрического строения кристаллов выявилось, что их атомы расположены очень правильным образом,
- 5. Бесконечная плоская фигура Ф называется плоским орнаментом, если выполнены следующие условия: (1) среди перемещений, отображающих Ф
- 6. Если плоская фигура отображается сама на себя при параллельных переносах только одного направления (и противоположному ему),
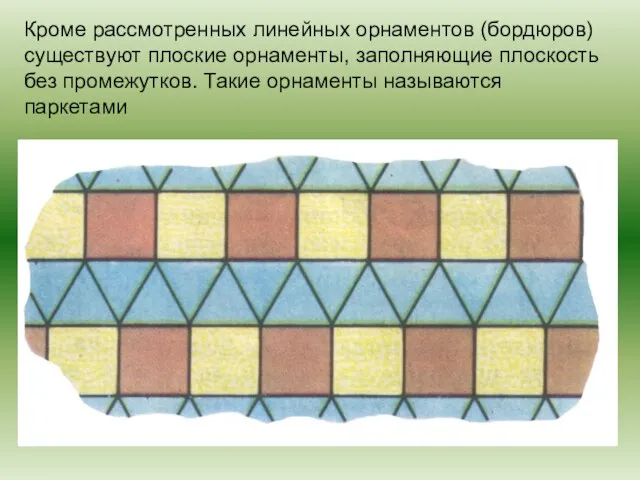
- 7. Кроме рассмотренных линейных орнаментов (бордюров) существуют плоские орнаменты, заполняющие плоскость без промежутков. Такие орнаменты называются паркетами
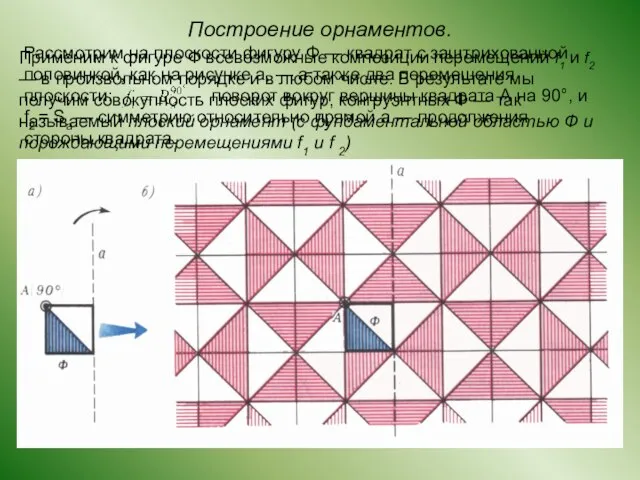
- 8. Рассмотрим на плоскости фигуру Ф — квадрат с заштрихованной половинкой, как на рисунке а, — а
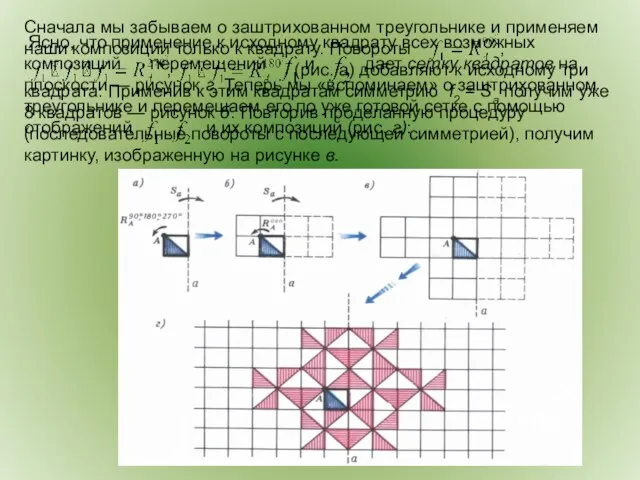
- 9. Сначала мы забываем о заштрихованном треугольнике и применяем наши композиции только к квадрату. Повороты , ,
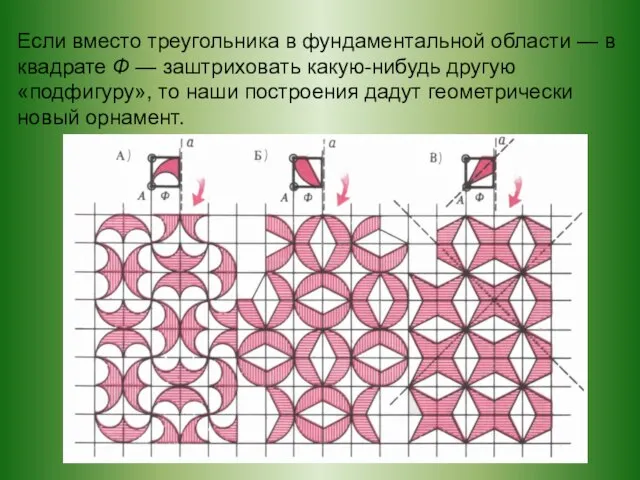
- 10. Если вместо треугольника в фундаментальной области — в квадрате Ф — заштриховать какую-нибудь другую «подфигуру», то
- 11. Это орнаменты разных типов: их группы симметрии устроены по-разному (имеют разные сетки осей симметрии или разные
- 12. Если добавить к этим орнаментам еще два, то получится полный «атлас» плоских орнаментов! Оказывается, существует только
- 13. Уравнения орнаментов. Под математическим орнаментом мы будем понимать рисунок, характеризуемым каким – либо уравнением или неравенством
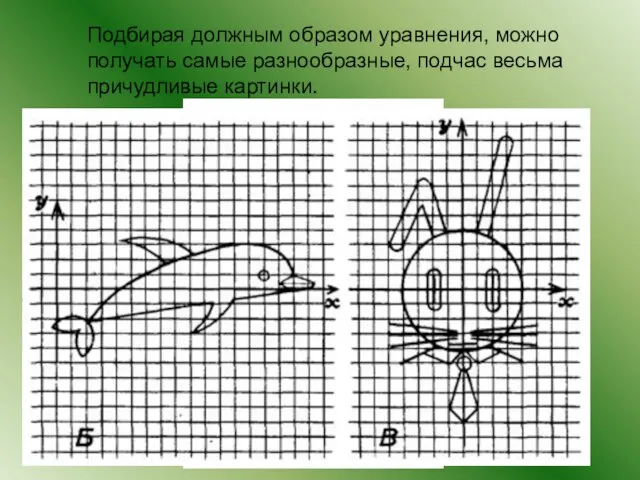
- 14. Подбирая должным образом уравнения, можно получать самые разнообразные, подчас весьма причудливые картинки.
- 15. Посмотрим как они получаются. Линейный орнамент получается с помощью переносов некоторой основной фигуры вдоль некоторого направления.
- 17. Скачать презентацию









 Магнит ММ 02 06 2022г
Магнит ММ 02 06 2022г Фанерование. Цель фанерования
Фанерование. Цель фанерования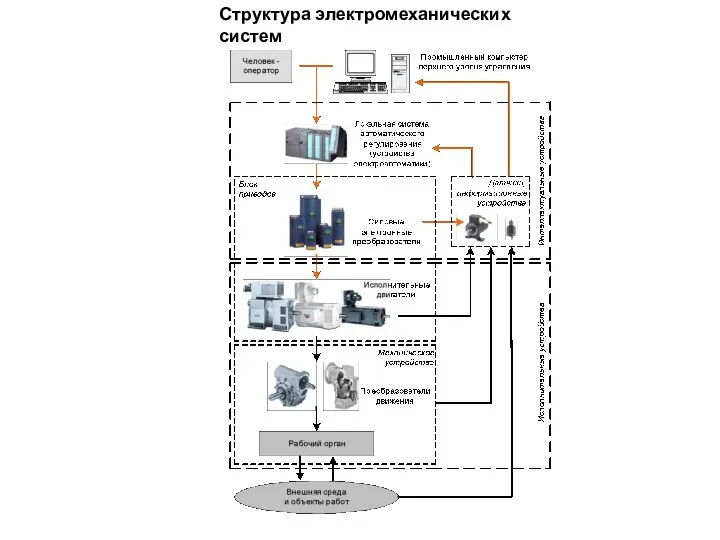 Структура электромеханических систем
Структура электромеханических систем Презентация на тему: Помпеи
Презентация на тему: Помпеи Права человека и гражданина
Права человека и гражданина РГКП «Алматинский музыкальный колледж им. П. Чайковского»
РГКП «Алматинский музыкальный колледж им. П. Чайковского» 70-летиюРостовской областипосвящается
70-летиюРостовской областипосвящается История письменности на Руси
История письменности на Руси Сущность финансового менеджмента
Сущность финансового менеджмента Атомные электростанции
Атомные электростанции 25 октября - День флага Донецкой Народной Республики
25 октября - День флага Донецкой Народной Республики Ультрафиолетовые лучи
Ультрафиолетовые лучи Проблемы стран “третьего мира”
Проблемы стран “третьего мира” Разработка гибкого производственного модуля на базе токарного оборудования с ЧПУ
Разработка гибкого производственного модуля на базе токарного оборудования с ЧПУ rabota
rabota Решение логических задач
Решение логических задач Повседневная деятельность
Повседневная деятельность Азаматтық құқықтық обьектілері
Азаматтық құқықтық обьектілері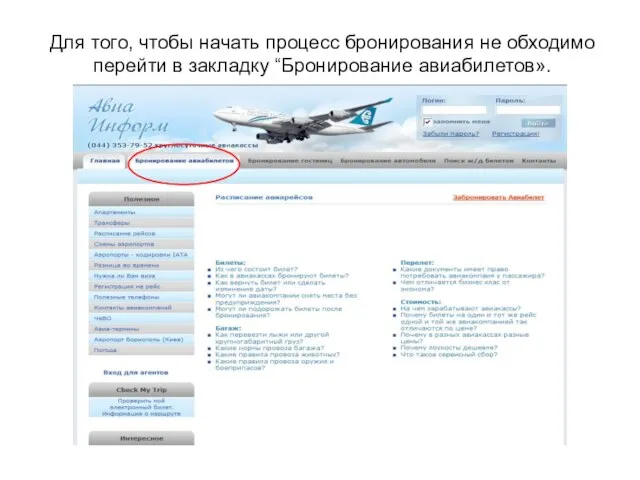 Для того, чтобы начать процесс бронирования не обходимо перейти в закладку “Бронирование авиабилетов».
Для того, чтобы начать процесс бронирования не обходимо перейти в закладку “Бронирование авиабилетов». Этические и юридические аспекты использования мультимедийных средств
Этические и юридические аспекты использования мультимедийных средств Стабильность финансовой системы в условиях кризиса
Стабильность финансовой системы в условиях кризиса Юрий Дмитриев Зелёное и жёлтое
Юрий Дмитриев Зелёное и жёлтое Имя прилагательное. 3 класс
Имя прилагательное. 3 класс Презентация на тему Растровое кодирование графической информации
Презентация на тему Растровое кодирование графической информации Дальний Восток
Дальний Восток Налогообложение в России
Налогообложение в России Минск, 2010
Минск, 2010 Общие сведения о МВЗ армий иностранных государств
Общие сведения о МВЗ армий иностранных государств