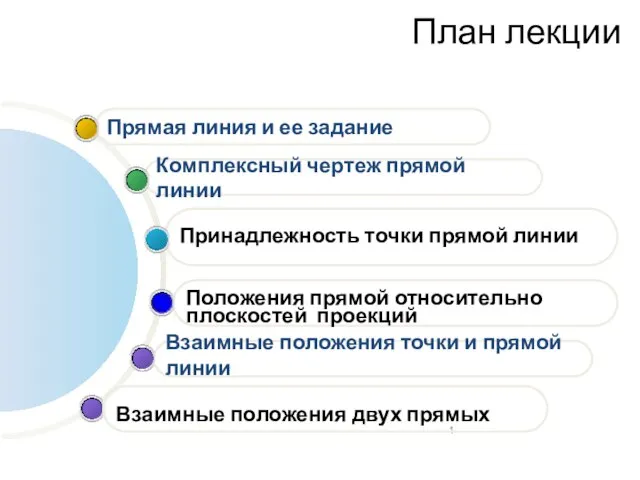
Содержание
- 2. Взаимные положения точки и прямой линии Принадлежность точки прямой линии Комплексный чертеж прямой линии Прямая линия
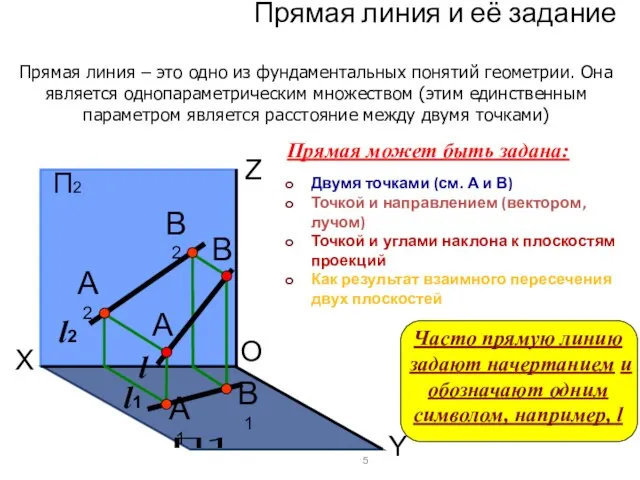
- 3. Прямая линия и её задание Прямая линия – это одно из фундаментальных понятий геометрии. Она является
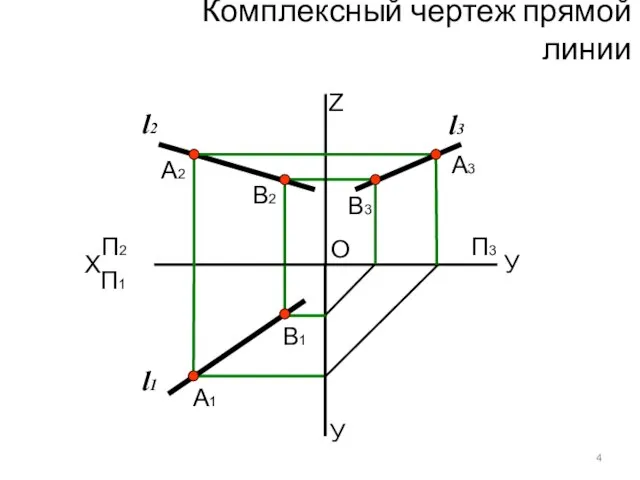
- 4. X У У А1 O П2 Z А2 П1 П3 А3 Комплексный чертеж прямой линии В1
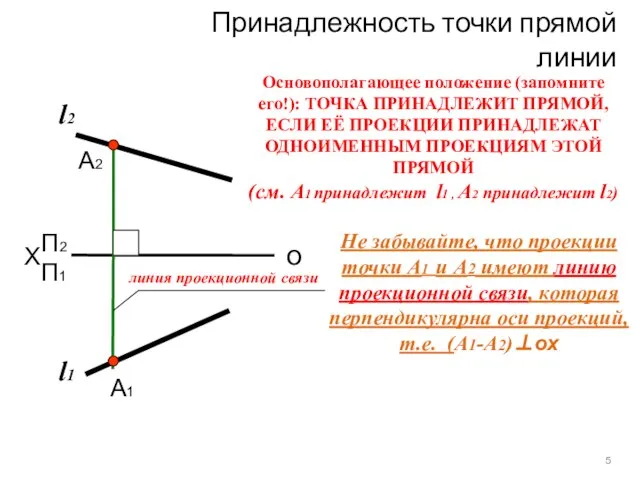
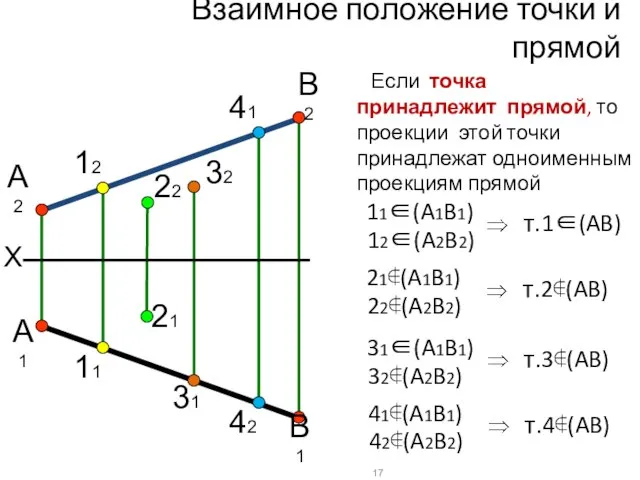
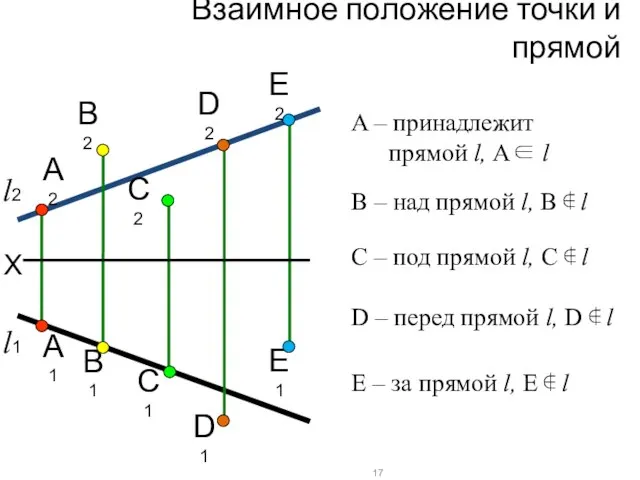
- 5. Принадлежность точки прямой линии Основополагающее положение (запомните его!): ТОЧКА ПРИНАДЛЕЖИТ ПРЯМОЙ, ЕСЛИ ЕЁ ПРОЕКЦИИ ПРИНАДЛЕЖАТ ОДНОИМЕННЫМ
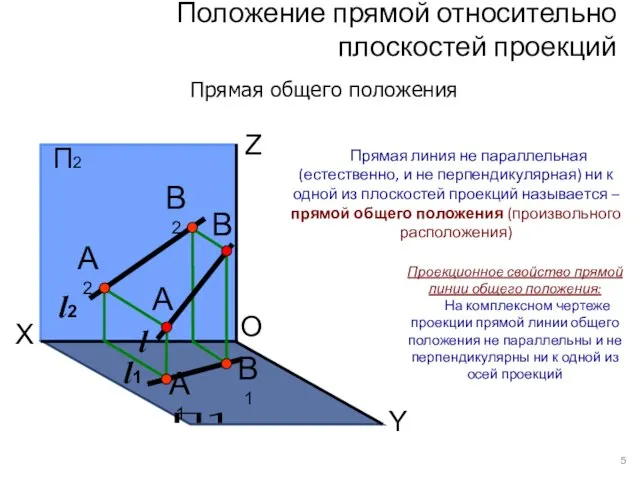
- 6. Положение прямой относительно плоскостей проекций Прямая общего положения Прямая линия не параллельная (естественно, и не перпендикулярная)
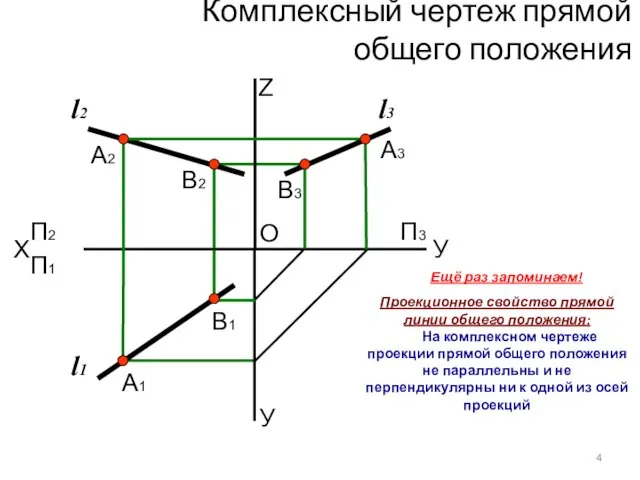
- 7. Комплексный чертеж прямой общего положения 4 Ещё раз запоминаем! Проекционное свойство прямой линии общего положения: На
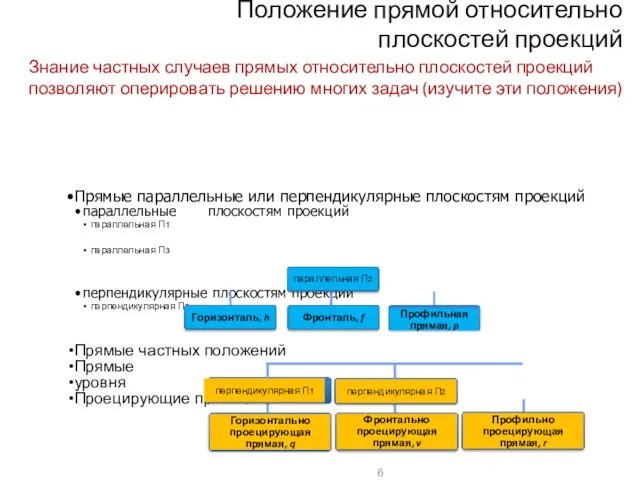
- 8. Положение прямой относительно плоскостей проекций Прямые параллельные или перпендикулярные плоскостям проекций параллельные плоскостям проекций параллельная П1
- 9. Прямой уровня называется прямая, параллельная к одной из плоскостей проекций. Положение прямой относительно плоскостей проекций Прямые
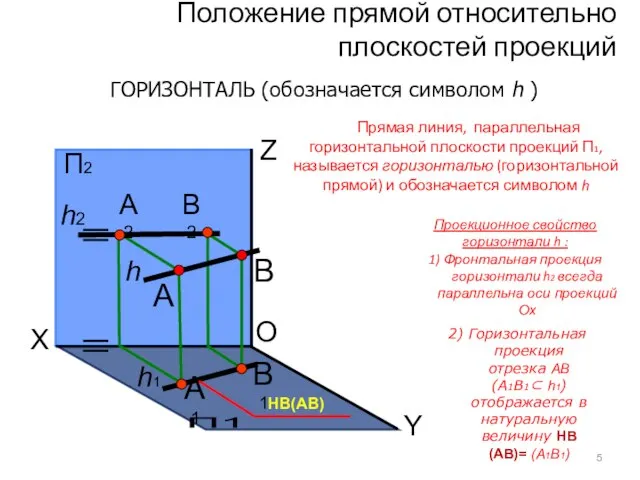
- 10. Положение прямой относительно плоскостей проекций ГОРИЗОНТАЛЬ (обозначается символом h ) O П2 П1 X Y Z
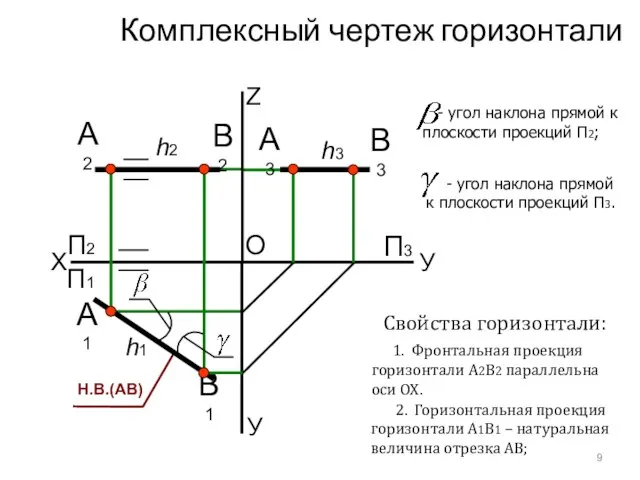
- 11. Комплексный чертеж горизонтали X У А1 O П2 Z А2 П1 П3 А3 В1 В2 В3
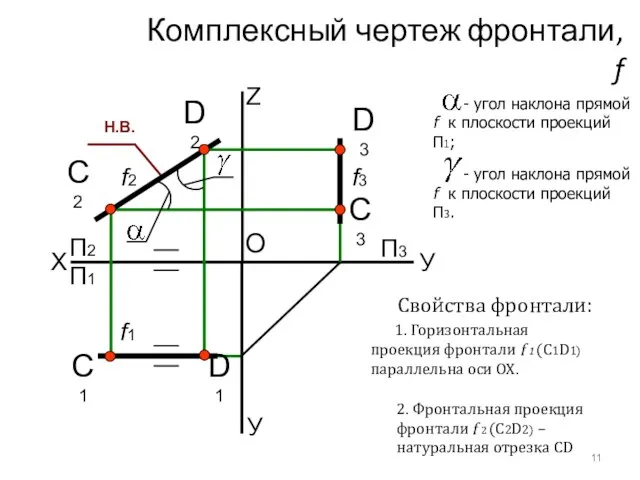
- 12. Комплексный чертеж фронтали, f X У C1 O П2 Z С2 П1 П3 C3 D1 D2
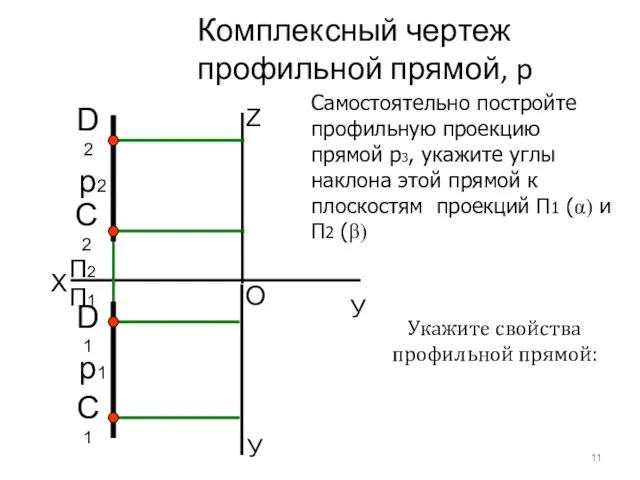
- 13. Комплексный чертеж профильной прямой, p X У C1 O П2 Z С2 П1 D1 D2 Самостоятельно
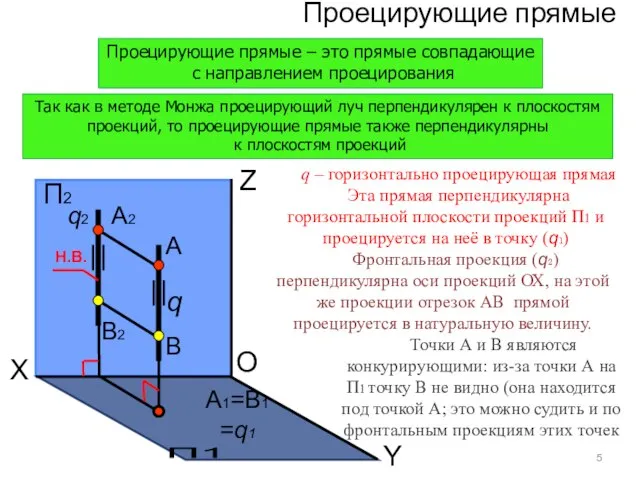
- 14. Проецирующие прямые O П2 П1 X Y Z А1=B1 =q1 А А2 В В2 q –
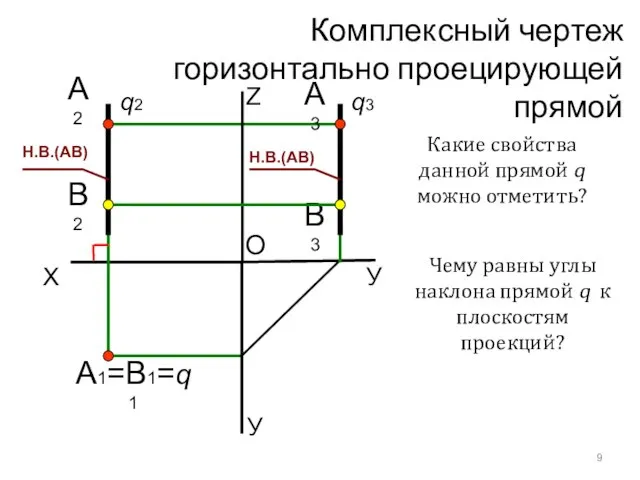
- 15. Комплексный чертеж горизонтально проецирующей прямой X У А1=B1=q1 O Z А2 А3 В2 В3 Н.В.(АВ) Какие
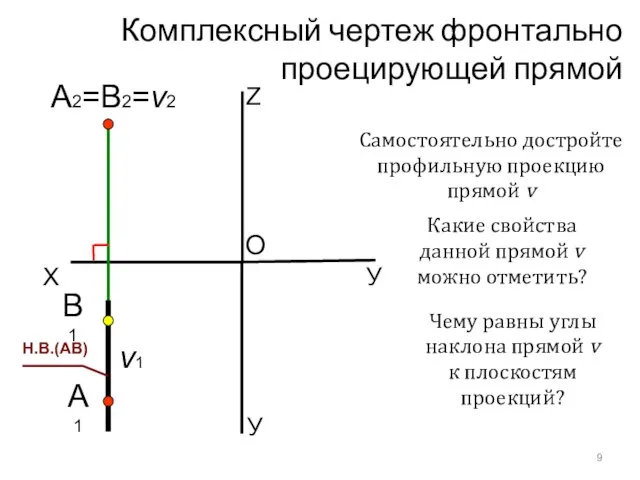
- 16. Комплексный чертеж фронтально проецирующей прямой X У А2=B2=v2 O Z А1 В1 Н.В.(АВ) Какие свойства данной
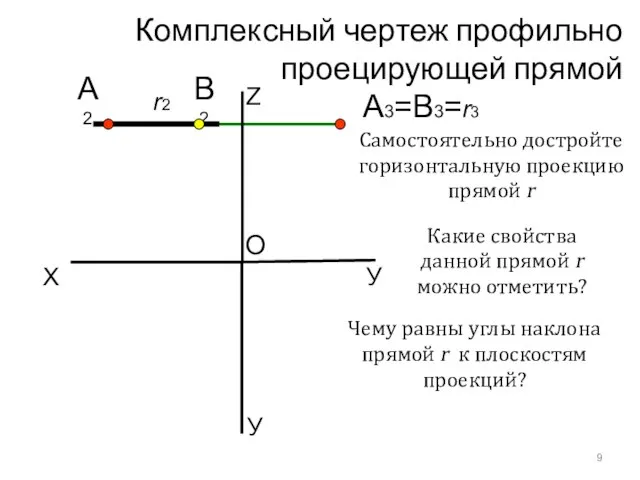
- 17. Комплексный чертеж профильно проецирующей прямой X У А3=B3=r3 O Z А2 В2 Какие свойства данной прямой
- 18. Взаимное положение точки и прямой X А2 В2 А1 В1 12 11 22 21 32 31
- 19. Взаимное положение точки и прямой X А2 E2 А1 E1 B2 B1 C2 C1 D2 D1
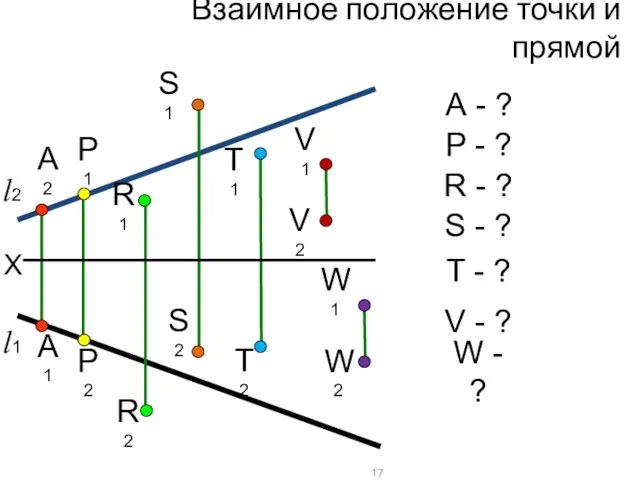
- 20. Взаимное положение точки и прямой X А2 T1 А1 T2 P1 P2 R1 R2 S1 S2
- 21. Взаимное расположение двух прямых Прямые в пространстве могут быть: Пересекающимися Параллельными Скрещивающимися 2
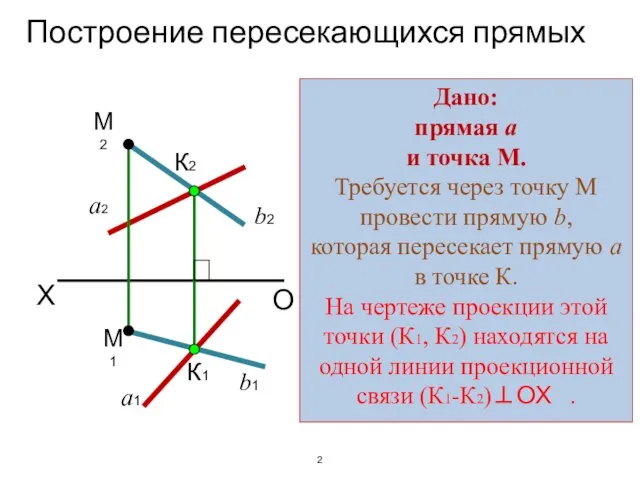
- 22. Пересекающиеся прямые Пересекающиеся прямые – это прямые имеющие одну общую собственную точку, т.е. точку их взаимного
- 23. Построение пересекающихся прямых 2 К1 К2 X a1 a2 b1 b2 Дано: прямая a и точка
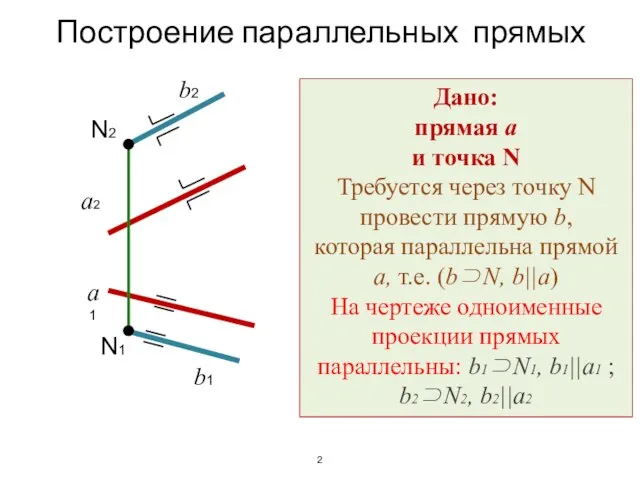
- 24. Параллельные прямые Параллельные прямые – это прямые имеющие одну общую несобственную точку (бесконечно удаленную точку) На
- 25. Построение параллельных прямых 2 a1 a2 b1 b2 Дано: прямая a и точка N Требуется через
- 26. Скрещивающиеся прямые Скрещивающиеся прямые – это прямые не имеющие общей точки На скрещивающихся прямых линиях рассматривают
- 28. Скачать презентацию





 Некоторые задачи технико-экономического анализа и оптимизации систем теплоснабжения .
Некоторые задачи технико-экономического анализа и оптимизации систем теплоснабжения . Реформы Петра I
Реформы Петра I Логические операции
Логические операции Разработка домашнего задания на тему: матрешка
Разработка домашнего задания на тему: матрешка Презентация на тему Объёмы геометрических тел
Презентация на тему Объёмы геометрических тел  Конституционное право
Конституционное право 20161006_tema_uroka_5_klass_svyaz_muzyki_i_literatury
20161006_tema_uroka_5_klass_svyaz_muzyki_i_literatury Тема: Природные экосистемы, взаимоотношения между компонентами экосистемы. Антропологические аксиомы
Тема: Природные экосистемы, взаимоотношения между компонентами экосистемы. Антропологические аксиомы Правописание безударных гласных
Правописание безударных гласных Текстовый документ
Текстовый документ БИОМЫ ОСТРОВОВ
БИОМЫ ОСТРОВОВ Россия – Англия:2 : 1
Россия – Англия:2 : 1 Вокруг Пушкина
Вокруг Пушкина Антивирусные программы
Антивирусные программы Криминологичекая характеристика тяжких преступлений против личности
Криминологичекая характеристика тяжких преступлений против личности British Mass Media
British Mass Media Южный Федеральный Университет Факультет социологии и политологии Презентация лекции по семестровому курсу социологии Для бака
Южный Федеральный Университет Факультет социологии и политологии Презентация лекции по семестровому курсу социологии Для бака Компетенции учителя искусства
Компетенции учителя искусства Сводный студенческий отряд проводников Жигули
Сводный студенческий отряд проводников Жигули Презентация на тему: Школа в условиях подготовки к внедрению ФГОС второго поколения образования
Презентация на тему: Школа в условиях подготовки к внедрению ФГОС второго поколения образования Концептуальное основание современного В2В маркетинга. Концепция маркетинга взаимодействия
Концептуальное основание современного В2В маркетинга. Концепция маркетинга взаимодействия Wolfgang Amadeus Mozart
Wolfgang Amadeus Mozart Историко-культурные достопримечательности Республики Хакасия ( игра – викторина )
Историко-культурные достопримечательности Республики Хакасия ( игра – викторина ) Государственные и муниципальные финансы. Решение задач
Государственные и муниципальные финансы. Решение задач Рисуем музыку
Рисуем музыку Законодательство Российской Федерации в области инклюзивного образования
Законодательство Российской Федерации в области инклюзивного образования Настольный теннис
Настольный теннис Подробное изложение "Первый снег"
Подробное изложение "Первый снег"