1_Introduction(1)

План
Вычислительная математика
Моделирование
Методы в схеме вычислительного эксперимента
Структура погрешности
Корректность, устойчивость и сходимость
Инструменты реализации вычислительных методов

Вычислительная математика
Вычислительная математика - область численного решения задач, возникающих в процессе компьютерного математического моделирования
Вычислительные науки — быстроразвивающаяся междисциплинарная область. В ней используются передовые вычислитель- ные возможности для решения различных проблем.
Например:
Вычислительная геномика
сравнивает цепочки и расшифровывает последовательности генов с помощью сложных статистических методов и алгоритмов машинного обучения
Вычислительная химия
Сфера применения: моделирует поведение молекул и прогнозирует реакции с помощью математических методов

Понятие о моделировании
Модель – это идеальный образ или материальный прообраз системы (оригинала данной модели), подобный ей в конечном числе отношений, который в определенных условиях может заменять объект-оригинал, воспроизводя интересующие нас свойства и характеристики оригинала.
Модель концентрирует в себе записанную на определенном языке (естественном, алгоритмическом, математическом) совокупность наших знаний, представлений и гипотез о соответствующем объекте или системе.

Модель и оригинал
Модель подобна оригиналу в конечном числе отношений.
Модель проще оригинала.
модель только приближенно отображает оригинал.
Модель, с помощью которой успешно достигается цель моделирования, будем называть адекватной.

Моделирование
Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием.
Моделирование может быть:
натурным (физическим),
математическим,
комбинированным.

Натурное моделирование
Исследуемая система заменяется соответствующей ей другой материальной системой, которая воспроизводит свойства изучаемой системы с сохранением их физической природы.
Примером этого вида моделирования может служить пилотная компьютерная сеть.

Математическое моделирование
Математическая модель представляет собой совокупность соотношений (формул, уравнений, неравенств, логических условий), определяющих процесс изменения состояния системы в зависимости от ее параметров, входных сигналов, начальных условий и времени.
Математическое моделирование может быть аналитическое и имитационное.

Аналитическое моделирование
Процессы функционирования элементов системы записываются в виде некоторых математических соотношений (алгебраических, дифференциальных) или логических условий. Однако подобную модель можно построить только для сравнительно простых систем.

Имитационное моделирование
Вид компьютерного моделирования, для которого характерно воспроизведение на ЭВМ (имитация) процесса функционирования исследуемой сложной системы. Такие модели представляют собой компьютерную программу, которая шаг за шагом воспроизводит события, происходящие в реальной системе.

Типы математических моделей
Дифференциальные – задача описывается дифференциальным уравнением или их системой.
Рекуррентные – значение параметров в следующий момент времени выражается через предыдущие состояния.
Матричные – задача сводится к построению матрицы или набора матриц.
Вероятностные – моделируется с использованием случайных факторов.

Комбинированное моделирование
Типичным примером комбинированного моделирования является исследование динамики летательного аппарата на комплексе из математической модели движения самого аппарата, воспроизводимой на ЭВМ, и макета реальной аппаратуры управления

Методы в схеме
вычислительного эксперимента
Основной целью моделирования является постановка над моделью экспериментов с последующей интерпретацией результатов для моделируемой системы. Вычислительный эксперимент проводится не над реальным объектом, а над его математической моделью, и роль экспериментальной установки играет оснащенная специально разработанной программой ЭВМ.

Вычислительный эксперимент
Имеет ряд преимуществ:
дешевле физического;
можно легко и безопасно вмешиваться;
можно повторить и прервать в любой момент;
можно смоделировать условия, которые не получается воссоздать в лаборатории.

Численные методы
– это методы приближенного решения задач на ЭВМ, которые не могут быть решены аналитическим способом (точно) или их решение требует слишком больших затрат. Общим для всех численных методов является сведение математической задачи к конечномерной.

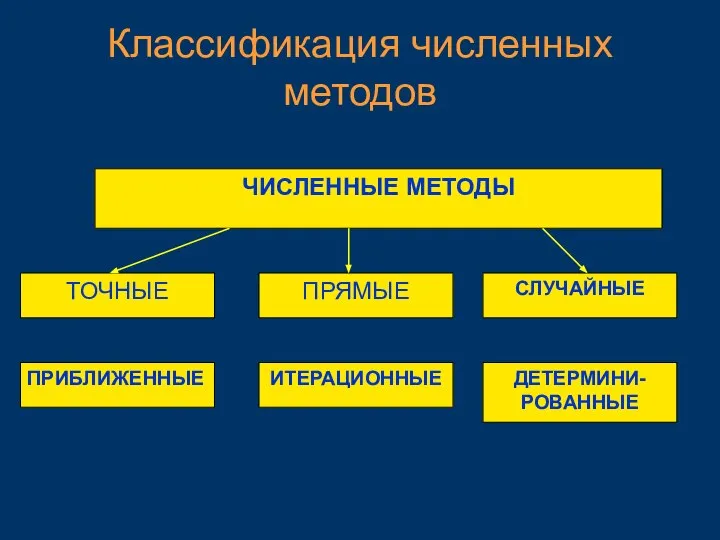
Классификация численных методов
ЧИСЛЕННЫЕ МЕТОДЫ
ТОЧНЫЕ
ПРИБЛИЖЕННЫЕ
ПРЯМЫЕ
ИТЕРАЦИОННЫЕ
СЛУЧАЙНЫЕ
ДЕТЕРМИНИ-
РОВАННЫЕ

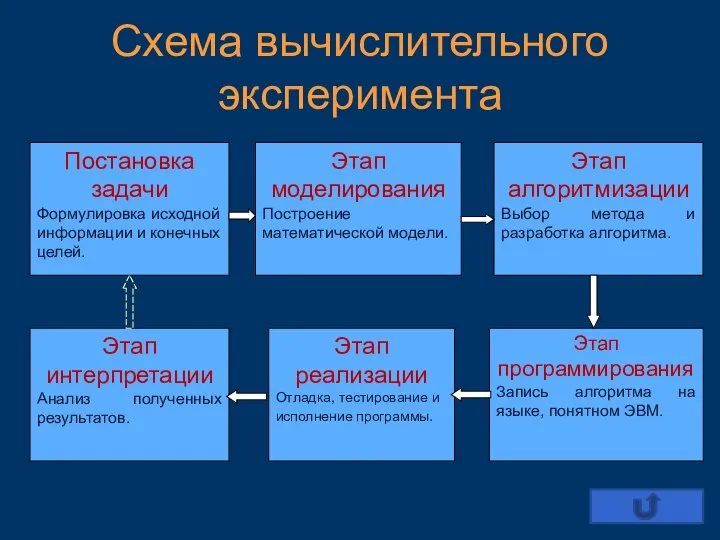
Схема вычислительного эксперимента
Постановка
задачи
Формулировка исходной информации и конечных целей.
Этап моделирования
Построение математической модели.
Этап алгоритмизации
Выбор метода и разработка алгоритма.
Этап реализации
Отладка, тестирование и исполнение программы.
Этап интерпретации
Анализ полученных результатов.
Этап программирования
Запись алгоритма на языке, понятном ЭВМ.

Структура погрешности
Погрешность исходных данных (неустранимая).
Погрешность модели.
Погрешность метода.
Вычислительная погрешность.

Корректность
Задача называется корректно поставленной, если для любых значений исходных данных из некоторого допустимого множества ее решение существует, единственно и устойчиво по начальным данным.

Устойчивость
Устойчивость по начальным данным означает, что малым изменениям исходных данных соответствует незначительное изменение результата (в применении к устойчивым реальным процессам). Устойчивость метода трактуется аналогично – малым ошибкам округления соответствует малые изменения результата.

Сходимость
Численный метод сходится к точному решению задачи, если при неограниченном росте параметра дискретизации решение дискретной задачи стремиться к решению исходной задачи. Необходимость получения результата с любой заранее заданной точностью за конечное число шагов требует использования быстро сходящихся методов.

Инструменты реализации вычислительных методов
Электронные таблицы
Пакеты для математических расчетов
Языки программирования и СПО

Электронные таблицы
Microsoft Excel
OpenOffice Calc
Lotus 1-2-3
Quattro Pro

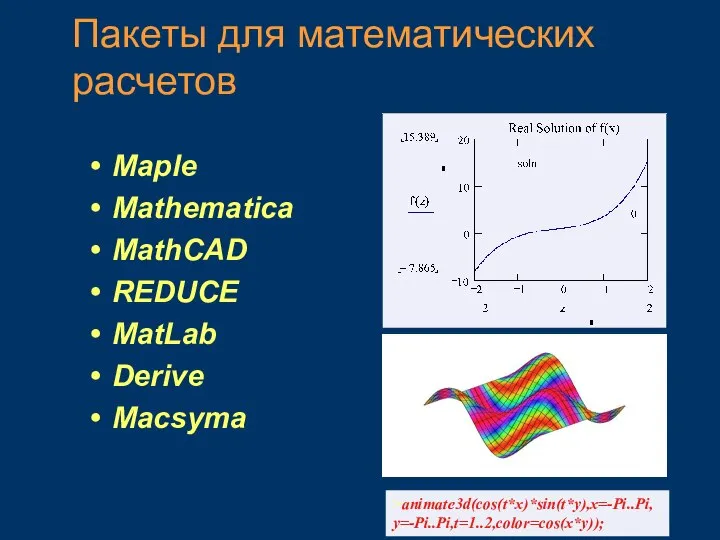
Пакеты для математических расчетов
Maple
Mathematica
MathCAD
REDUCE
MatLab
Derive
Macsyma
>animate3d(cos(t*x)*sin(t*y),x=-Pi..Pi, y=-Pi..Pi,t=1..2,color=cos(x*y));