2.10.Колебания поверхностных атомов

Приближение Дебая
Приближение Дебая
ωD=qDvзв

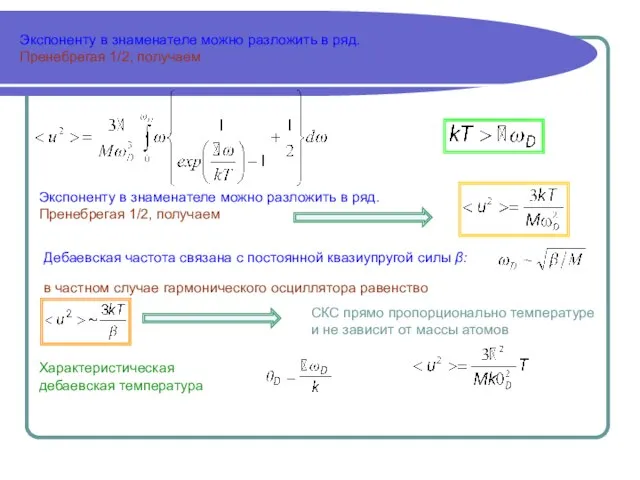
Экспоненту в знаменателе можно разложить в ряд.
Пренебрегая 1/2, получаем
Экспоненту в знаменателе можно разложить в ряд.
Пренебрегая 1/2, получаем
Дебаевская частота связана с постоянной квазиупругой силы β:
в частном случае гармонического осциллятора равенство
СКС прямо пропорционально температуре
и не зависит от массы атомов
Характеристическая
дебаевская температура

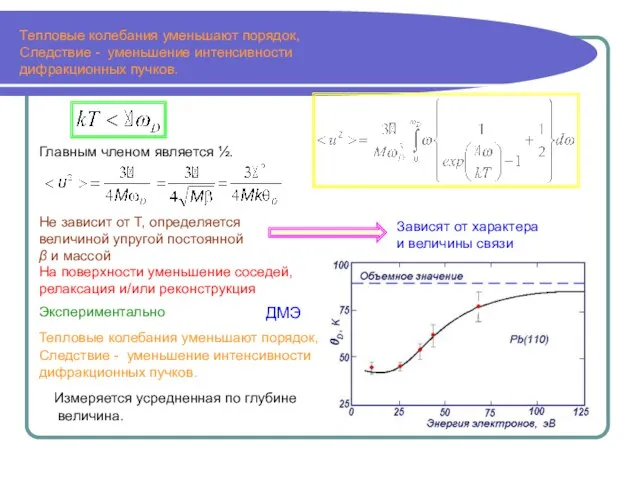
Тепловые колебания уменьшают порядок,
Следствие - уменьшение интенсивности
дифракционных пучков.
Тепловые колебания уменьшают порядок,
Следствие - уменьшение интенсивности
дифракционных пучков.
Измеряется усредненная по глубине
величина.
Зависят от характера
и величины связи
На поверхности уменьшение соседей,
релаксация и/или реконструкция
Экспериментально
ДМЭ
Главным членом является ½.
Не зависит от Т, определяется
величиной упругой постоянной
β и массой

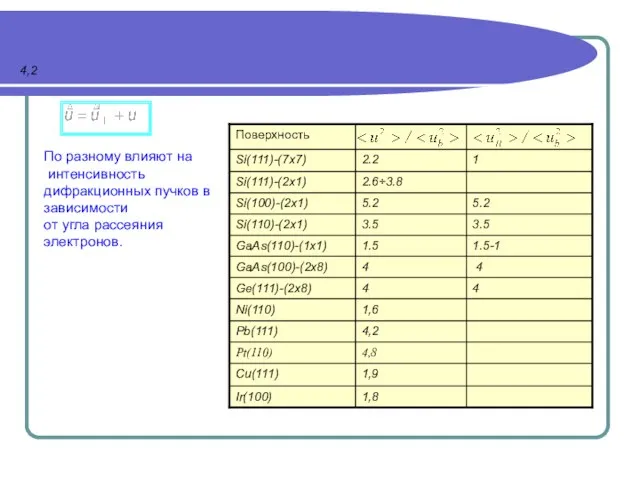
4,2
По разному влияют на
интенсивность
дифракционных пучков в
зависимости
от угла рассеяния электронов.

Термическое расширение
Следствие ангармонизма сил
F=-βx+γx2
Потенциальная энергия:
Вероятность отклонения атома
от равновесного положения
по статистике Больцмана:
Пусть
Постоянная А из условия

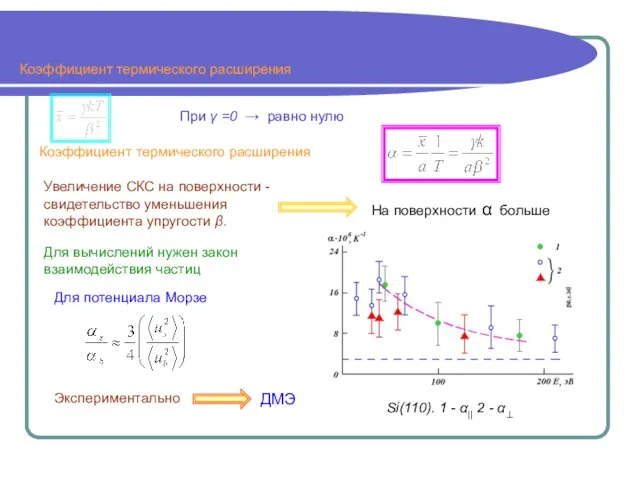
Коэффициент термического расширения
Коэффициент термического расширения
Увеличение СКС на поверхности -
свидетельство уменьшения
коэффициента упругости β.
На поверхности α больше
Для вычислений нужен закон
взаимодействия частиц
Для потенциала Морзе
Экспериментально
Si(110). 1 - α|| 2 - α⊥
При γ =0 → равно нулю
ДМЭ