5.5.Электропроводность тонких сплошных пленок

Кинетическое уравнение Больцмана
Кинетическое уравнение Больцмана
F и H – напряженности
электрического и магнитного поля
За счет изменения скорости под действием
сил со стороны внешних полей.
Справа находится величина, отражающая изменение функции распределения
за счет рассеяния
В стационарном случае устанавливается
стабильное значение функции распределения
Изменение распределения со временем
Изменение числа частиц в данном элементе объема за счет прихода из окружающих областей

Электрическое поле однородно
и действует вдоль оси х (F≡Fx)
Электрическое поле однородно
и действует вдоль оси х (F≡Fx)
Отклонение f от равновесной функции распределения f0,
соответствующей отсутствию внешних полей, не велико.
Удобно искать в виде
f = f0 + f1,
f1 - отклонение функции распределения от равновесия
Приближение времени релаксации
- время релаксации,
считается константой
Толщина пленка 2d << L
Допустим
Магнитное поле отсутствует (Н=0)

Выключим поле в момент t = 0
Выключим поле в момент t = 0
Система однородна
- время, характеризующее скорость
возвращения системы к состоянию равновесия
Пусть имеем однородную систему с установившимся в некотором внешнем поле
распределением электронов (f ≠ f0)
Уравнение Больцмана
Физический смысл τ можно установить рассматривая процесс
установления статистического равновесия

Стационарный случай (после завершения всех переходных процессов)
Стационарный случай (после завершения всех переходных процессов)
Однородность системы по координатам x и y
При малых Fx
f = f0 + f1

Умножим левую и правую части на
Умножим левую и правую части на
Граничное условие Фукса
Связывает отклонение от равновесного
распределения падающих на поверхность
электронов с отклонением отходящих от нее
Параметр Фукса

℘=0
℘=0
После столкновения с поверхностью
электрон забывает свою “предысторию”
Диффузное рассеяние
℘=1
Зеркальное отражение
.
℘=1, т.е. в случае зеркального отражения
Поверхность не влияет на
неравновесное распределение
Размерный эффект. отсутствует

Диффузное рассеяние
Диффузное рассеяние
Экспоненциальная зависимость от толщины пленки d и 1/vz
ρ - удельное сопротивление
d/λ>1
Тонкая пленка
λ - величина свободного пробега электрона
Толстая пленка
d/λ<<1

℘(ϑ) зависит от механизмов рассеяния электронов на поверхности
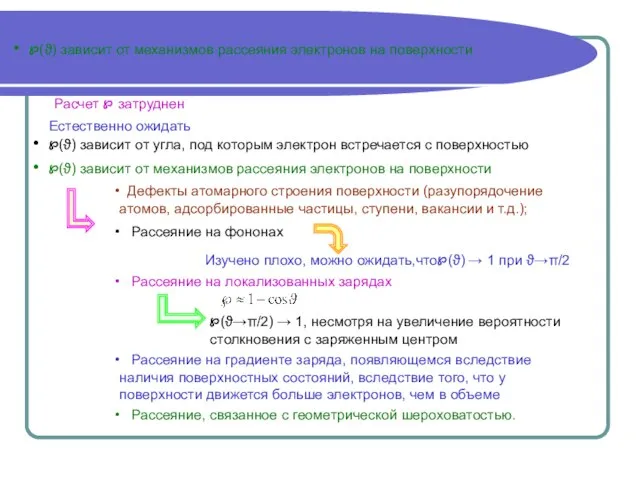
℘(ϑ) зависит от механизмов рассеяния электронов на поверхности
Расчет ℘ затруднен
Естественно ожидать
Дефекты атомарного строения поверхности (разупорядочение атомов, адсорбированные частицы, ступени, вакансии и т.д.);
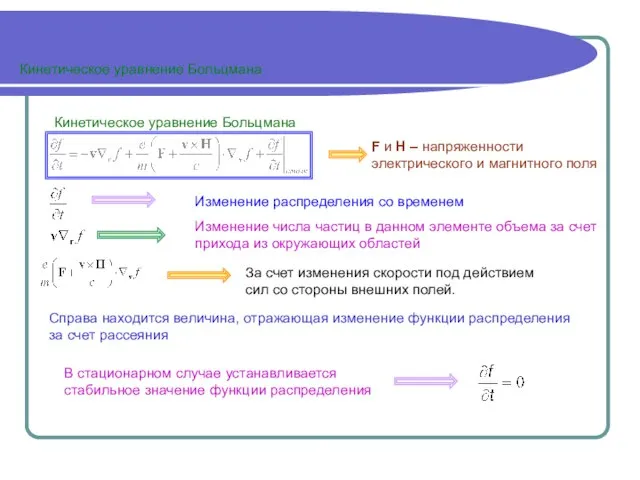
Рассеяние на фононах
Рассеяние на градиенте заряда, появляющемся вследствие наличия поверхностных состояний, вследствие того, что у поверхности движется больше электронов, чем в объеме
Рассеяние, связанное с геометрической шероховатостью.
Рассеяние на локализованных зарядах
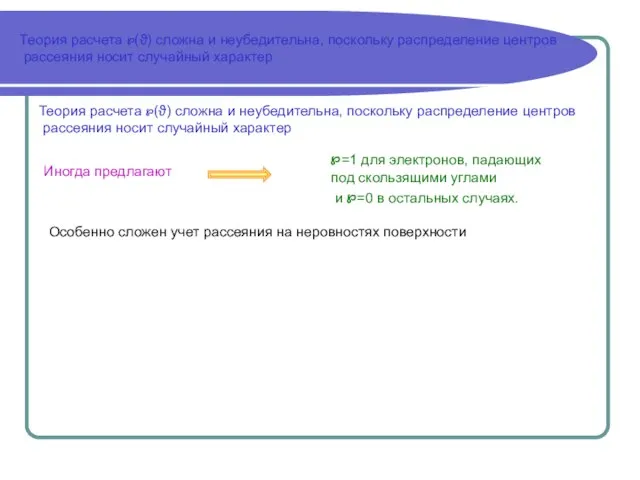
℘(ϑ→π/2) → 1, несмотря на увеличение вероятности
столкновения с заряженным центром
℘(ϑ) зависит от угла, под которым электрон встречается с поверхностью
Изучено плохо, можно ожидать,что℘(ϑ) → 1 при ϑ→π/2

Теория расчета ℘(ϑ) сложна и неубедительна, поскольку распределение центров
рассеяния носит случайный характер
Теория расчета ℘(ϑ) сложна и неубедительна, поскольку распределение центров
рассеяния носит случайный характер
℘=1 для электронов, падающих
под скользящими углами
и ℘=0 в остальных случаях.
Иногда предлагают
Особенно сложен учет рассеяния на неровностях поверхности