Содержание
- 2. ЛИНЕЙНАЯ ФУНКЦИЯ У=КХ+В И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ У=К/Х. АННОТАЦИЯ Проект разработан с использованием ИКТ и элементами модульной
- 3. План Аннотация. Цели. Ожидаемые результаты. Учебные вопросы. Теоретический материал. Проверочные работы. Критерии оценивания. Литература.
- 4. Цели изучив этот проект, учащиеся должны: -знать: основные функциональные понятия: понятие « функция», «график функции», «аргумент»,
- 5. Ожидаемые результаты обучения После завершения проекта учащиеся смогут: - назвать как минимум: что такое функция, график
- 6. Учебные вопросы - Что такое функция? (Зависимость одной переменной от другой называют функциональной зависимостью или функцией).
- 7. -Что такое прямая пропорциональность? (Прямой пропорциональностью называется функция, которую можно задать формулой вида у = кх,
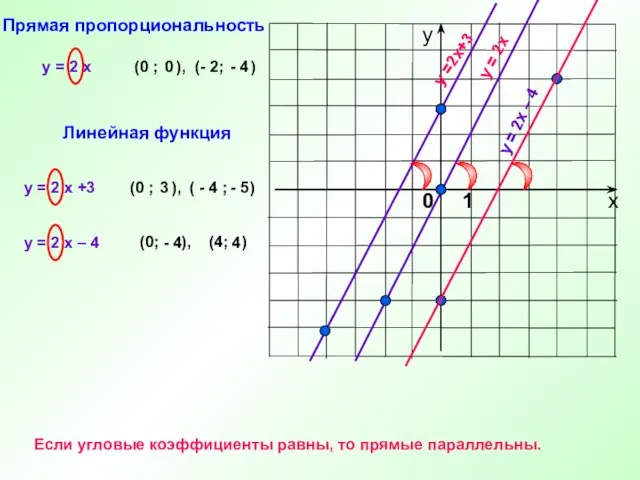
- 8. Линейной функцией называется функция вида у = kx + b где k и b – заданные
- 9. y = 2 x y = 2x y = 2 x +3 y =2x+3 (0 ;
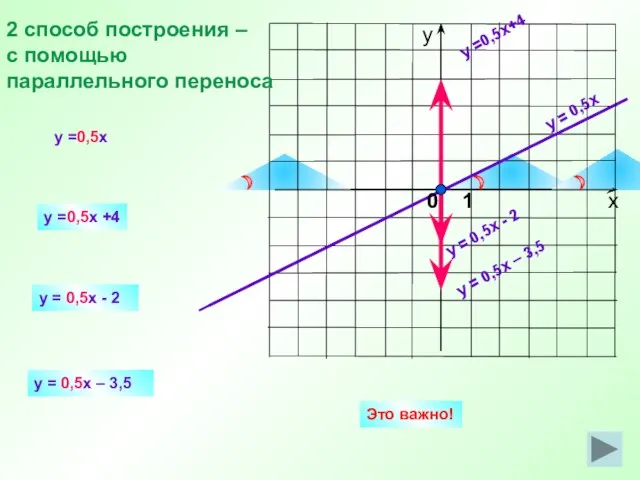
- 10. y = 0,5x y =0,5x+4 y = 0,5x - 2 y =0,5x +4 y = 0,5x
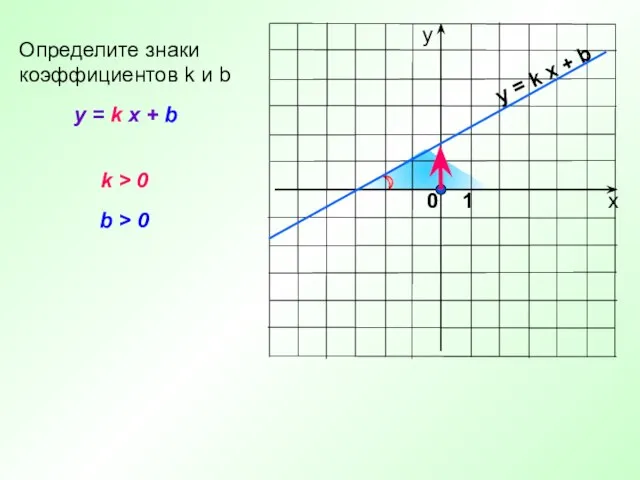
- 11. y = k x + b Определите знаки коэффициентов k и b k > 0 b
- 12. y = k x + b Определите знаки коэффициентов k и b k > 0 b
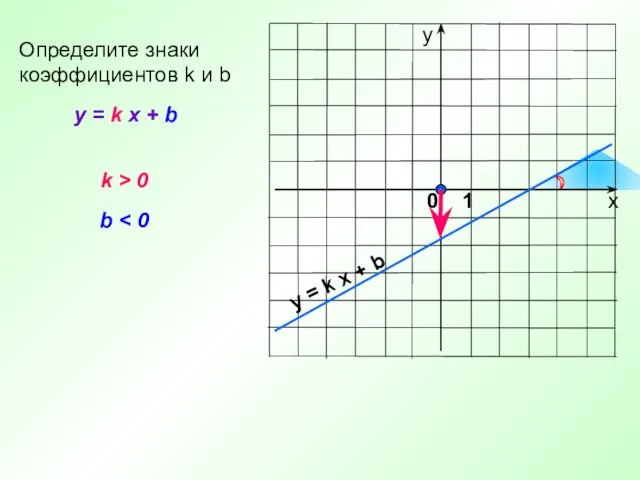
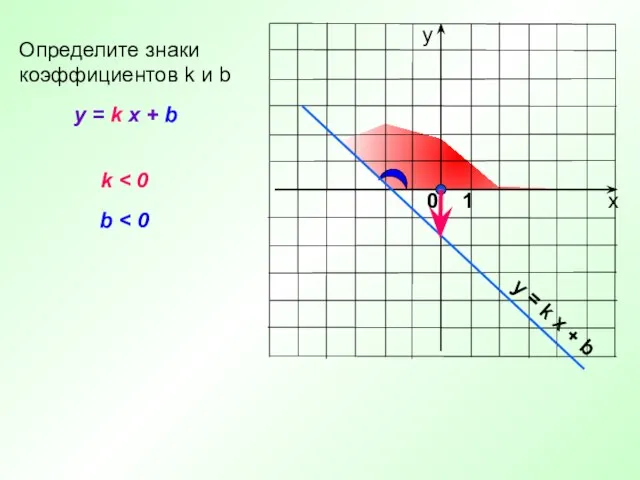
- 13. y = k x + b Определите знаки коэффициентов k и b k b y =
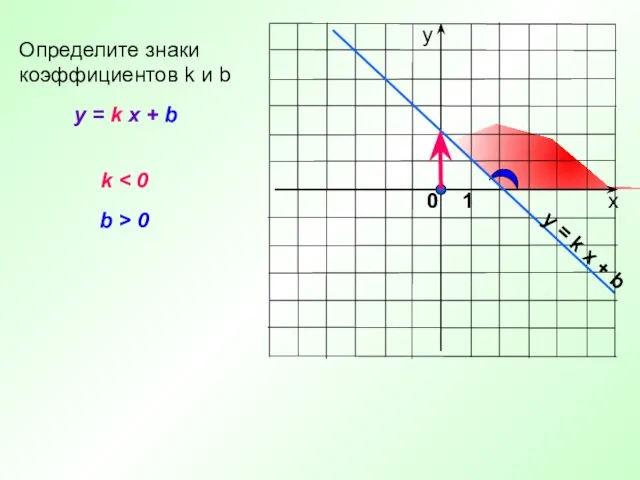
- 14. y = k x + b Определите знаки коэффициентов k и b k b > 0
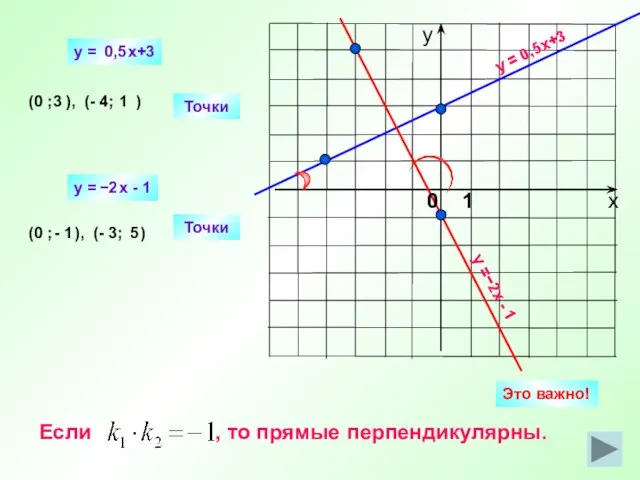
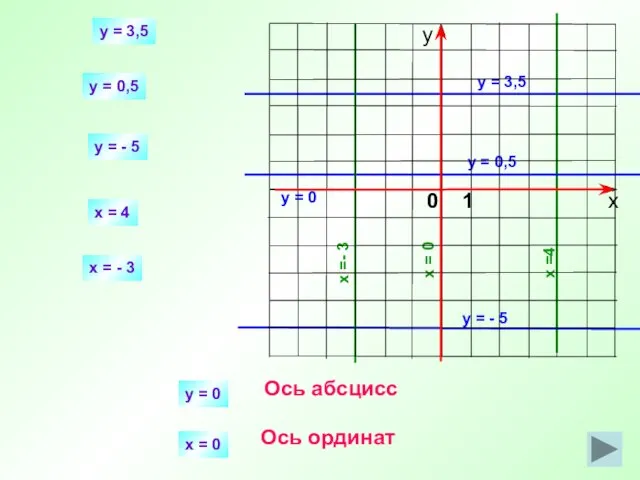
- 15. y = 0,5x+3 y =−2х - 1 Точки (0 ; ), (- 4; ) Точки (0
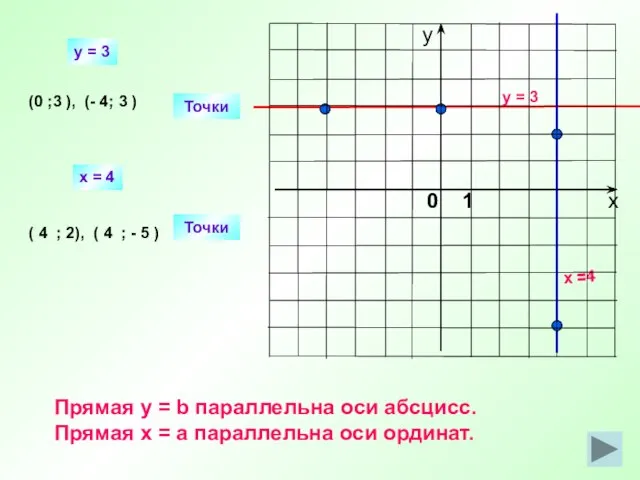
- 16. y = 3 x =4 Точки (0 ; ), (- 4; ) Точки ( ; 2),
- 17. y = 3,5 x =4 y = 3,5 x = 4 y = 0,5 y =
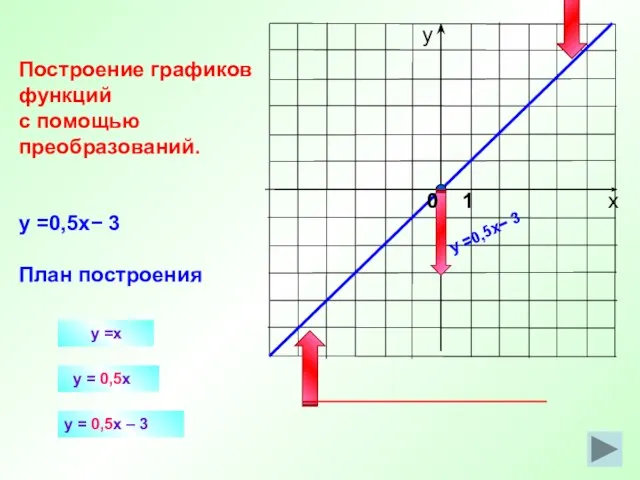
- 18. y =x y = 0,5x Построение графиков функций с помощью преобразований. y =0,5x− 3 План построения
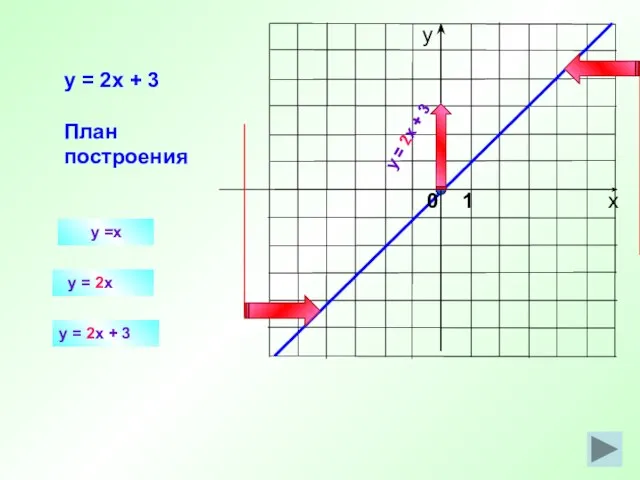
- 19. y =x y = 2x y = 2x + 3 План построения y = 2x +
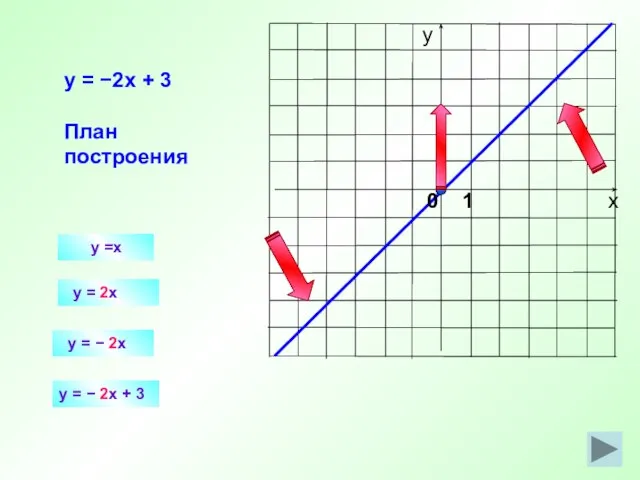
- 20. y =x y = 2x y = −2x + 3 План построения y = − 2x
- 21. Проверочная работа №1 Постройте график линейной функции: а) у=х+5; з) у=4; и) у=-3; б) у=-0,5х; к)у=2,5;
- 22. Постройте график функции, заданной следующим условием: а) значения у равны 1 при всех неположительных значениях х
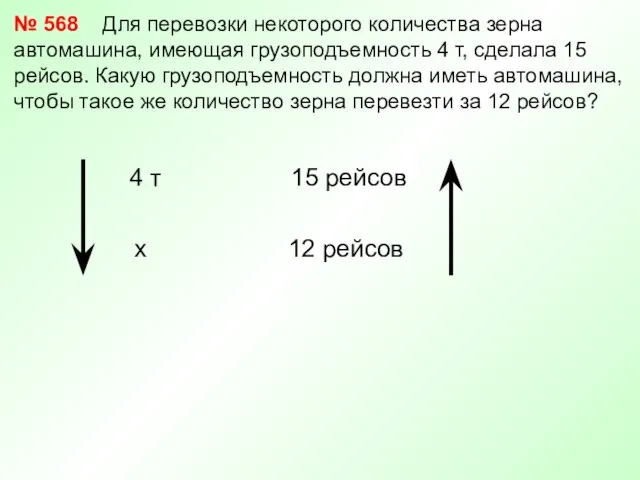
- 23. № 568 Для перевозки некоторого количества зерна автомашина, имеющая грузоподъемность 4 т, сделала 15 рейсов. Какую
- 24. Поезд движется из Москвы в Санкт-Петербург со скоростью v км/ч. За какое время поезд пройдет путь
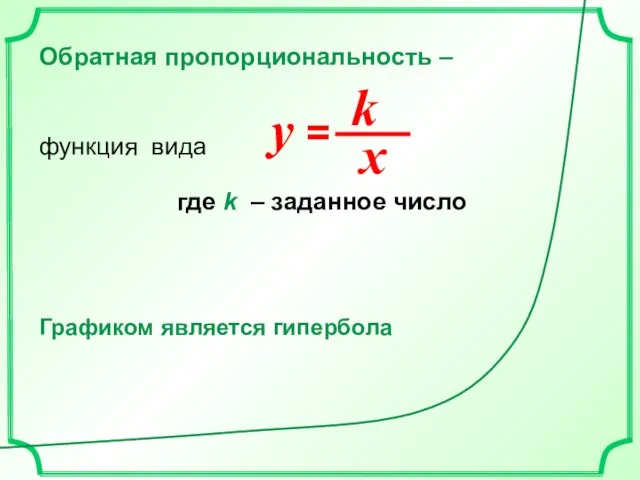
- 25. Обратная пропорциональность – функция вида где k – заданное число
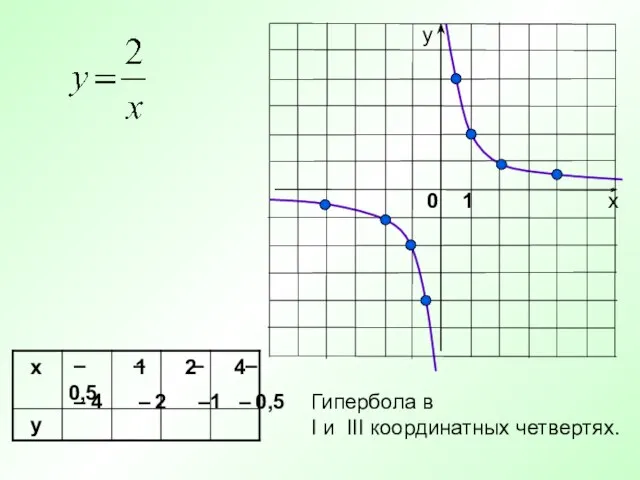
- 26. 1 Гипербола в I и III координатных четвертях. 4 2 0,5 0 1 – – –
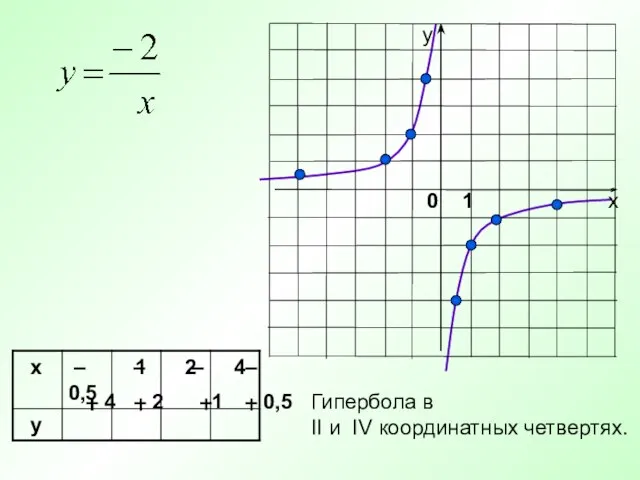
- 27. Гипербола в II и IV координатных четвертях. – 4 – – – – – 2 –1
- 28. Проверочная работа №2 Постройте график функции: а) у= 4/х; б) у=-4/х; в) у=8/х; г) у=-8/х. Постройте
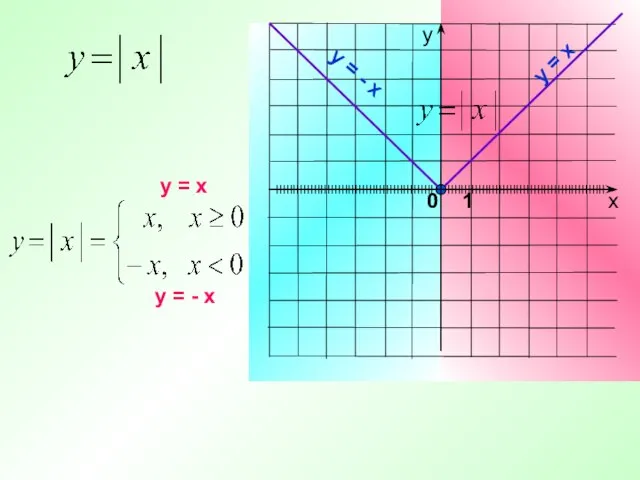
- 29. у = х у = - х IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII у = х IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII у = - х
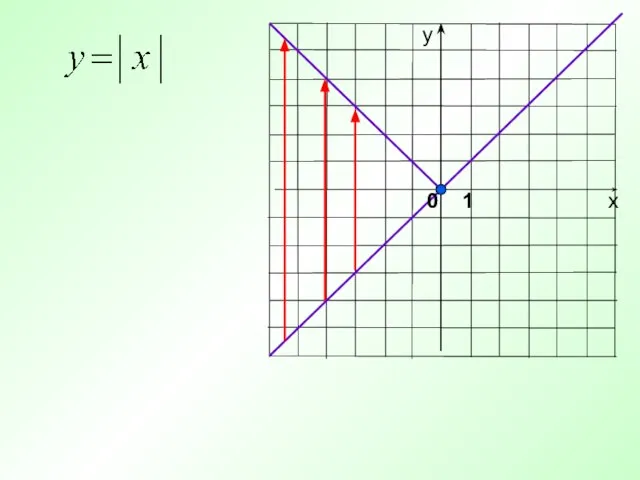
- 30. 0 1
- 31. Проверочная работа №3 Построить график функции: а) у=|х|; б) у=|х| + з; в) у= -|х| ;
- 32. Критерии оценивания Формы оценивания: промежуточное (формирующее) оценивание: - самооценка, взаимооценка участников проекта своей деятельности для выявления
- 34. Скачать презентацию













 1С-Битрикс Корпоративный портал 10.0 – 10.5
1С-Битрикс Корпоративный портал 10.0 – 10.5 Presentation Title
Presentation Title  Заседание ученого советаПОИПКРО
Заседание ученого советаПОИПКРО СОЦИАЛЬНЫЙ ПРОЕКТ «Там на ухоженных дорожках»
СОЦИАЛЬНЫЙ ПРОЕКТ «Там на ухоженных дорожках» Цель, Процесс, Результат
Цель, Процесс, Результат Гражданское право РФ. Право собственности и иные вещные права
Гражданское право РФ. Право собственности и иные вещные права Энергосбережение в нашей жизни УО «ВГПЛ1 машиностроения им. М.Ф.Шмырева» http://vgpl-1.iatp.by. - презентация
Энергосбережение в нашей жизни УО «ВГПЛ1 машиностроения им. М.Ф.Шмырева» http://vgpl-1.iatp.by. - презентация Интегрированное занятие « Математика + история»
Интегрированное занятие « Математика + история» Тестовые задания
Тестовые задания 3_Биологическая роль воды
3_Биологическая роль воды Презентация на тему Умножение одночлена на многочлен
Презентация на тему Умножение одночлена на многочлен  Иван Сергеевич Тургенев. Начало творческого пути писателя
Иван Сергеевич Тургенев. Начало творческого пути писателя Геометрическая абстракция
Геометрическая абстракция Угол. Сравнение углов. Биссектриса угла
Угол. Сравнение углов. Биссектриса угла Конфликты в семье
Конфликты в семье Вот он цветочек аленький
Вот он цветочек аленький Итоги 2003/2004 учебного года и задачи кафедр по повышению качества подготовки специалистов в новом учебном году Б.Е.Ды
Итоги 2003/2004 учебного года и задачи кафедр по повышению качества подготовки специалистов в новом учебном году Б.Е.Ды Витамин D
Витамин D Профессия Повар-кондитер
Профессия Повар-кондитер Неделя английского языка2011-2012
Неделя английского языка2011-2012 История математической логики
История математической логики Япония 11 класс
Япония 11 класс Склады и пункты приема поставок
Склады и пункты приема поставок Информационно-аналитический проект: Сто дней
Информационно-аналитический проект: Сто дней Тех. задание
Тех. задание Возможности развития познавательной мотивации учащихся.
Возможности развития познавательной мотивации учащихся. Николай Константинович Рерих (874 - 1947)
Николай Константинович Рерих (874 - 1947) Внешняя память компьютера
Внешняя память компьютера