7_tehnicheskaya_mehanika._para_sil.moment_pary.teoremy.usloviya_ravnovesiya

Пара сил. Момент пары.
Теорию пар разработал французский ученый-механик Л. Пуансо (1777-1859гг)

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил.
Система сил, образующих пара, не находится в равновесии.
Плоскостью действия пары называется плоскость, проходящая через линии действия пары сил.
Плечом пары называется расстояние α между линиями действия сил пары.

Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной, называемой моментом пары.

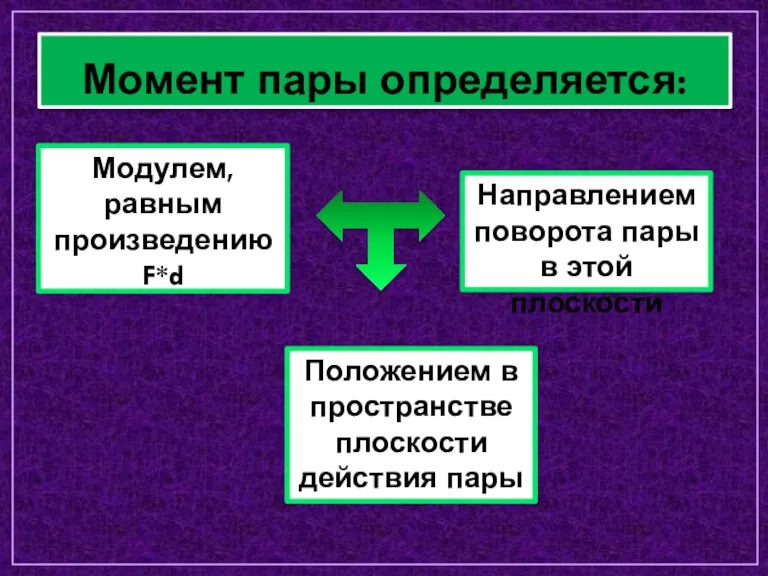
Момент пары определяется:
Модулем, равным произведению F*d
Положением в пространстве плоскости действия пары
Направлением поворота пары в этой плоскости

Момент пары может быть приложен в любой точке (такой вектор называется свободным).
Две пары сил, имеющие одинаковые моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие.

Теорема 1 - о сложении пар:

Свойства пары сил:
1. Пару, не изменяя оказываемого ею на твердое тело действия, можно переносить куда угодно в плоскости ее действия
2. У данной пары можно произвольно менять модули сил или длину плеча, сохраняя неизменным ее момент
3. Пару можно перенести из данной плоскости в любую другую плоскость, параллельную данной

Теорема 2:
Силу, приложенную к абсолютно твердому телу, можно переносить в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.
Действие силы при этом не изменится.

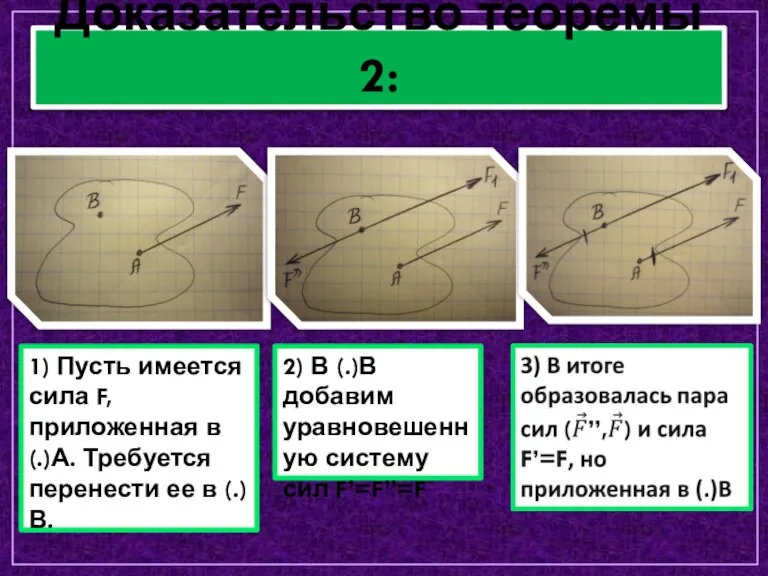
Доказательство теоремы 2:
1) Пусть имеется сила F, приложенная в (.)А. Требуется перенести ее в (.)В.
2) В (.)В добавим уравновешенную систему сил F’=F’’=F

Теорема 3:
Любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру заменяется одной силой, равной главному вектору системы сил и приложенной в центре приведения, и одной парой с моментом, равным главному моменту системы сил относительно центра

Теорема Вариньона:
Вариньон (1654-1722гг) франц. Физик, математик, механик
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен сумме моментов сил системы относительно того же центра.

Условия равновесия:
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю:
1

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких-нибудь двух центров (А и В) и сумма их проекций на ось Ох, не перпендикулярную прямой АВ, были равны нулю:
2
Условия равновесия:

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А,В и С, не лежащих на одной прямой, были равны нулю:
3
Условия равновесия:
(уравнения трех моментов)