Афинитивный анализ (теория и практика)

Аффинитивный анализ (affinity analysis) — методы исследования взаимной связи (ассоциаций) между событиями происходящими совместно и их количественная (т.е. в виде числа) оценка.
Результальт выполенния аффинитивного анализа – набор ассоциативных правил.
«affinity», в переводе означает «близость», «сходство».
Определение

Сфера применения
Торговая сфера. Для выявление наборов товаров, которые в супермаркетах часто покупаются вместе или никогда не покупаются вместе.
Медицина. Выявление причинно-следственных связей по возникновению побочных эффектов лекарств.
Производственная сфера. Выявление связи между параметрами оборудования и получаемыми качественными характеристиками продукта.
и многие другие сферы

Ключевое понятие – транзакция – множество событий происходящих одновременно (совместно)
Например: если мы анализируем деятельность торговой площадки, то в качестве транзакции можно рассматривать отдельный чек отдельного покупателя – совместная покупка отдельных товаров
Тогда проанализировав множество транзакций можно определить - является ли покупка одного товара следствием или причиной покупки другого товара. (клиент, купивший молоко, с вероятностью 75 % купит и хлеб)
Понятие транзакции

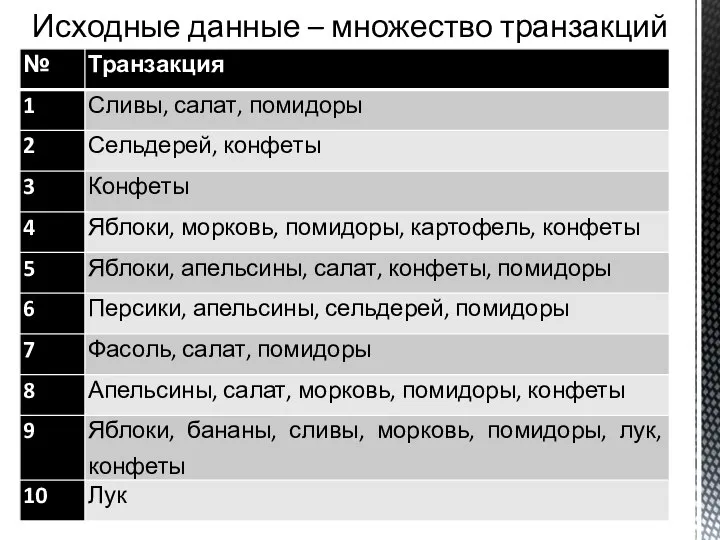
Исходные данные – множество транзакций

Ассоциативные правила
Импликация (бинарная логическая связка)
X→Y, где X⊂I, Y⊂I и X∩Y=⊘,
I – множество всех событий
T - транзакция
X – множества событий транзакции, называемых
условием (antecedent)
Y – множества событий транзакции, называемых
Следствием (consequent)
Читается правило: «Из X следует Y»

Связь между наборами предметов
X→Y
Ассоциативные правила описывают связь между
наборами событий X и Y.
Связь оценивается численно с помощью набора
показателей:
Основных:
Поддержка (support), обозначение S
Достоверность (confidence), обозначение С
и вспомогательных:
Лифт (lift), обозначение L
Левередж (leverage), обозначение T

Поддержка S (support) правила A→B, рассчитывается так:
Достоверность С (сonfidence) правила A→B,
рассчитывается так:
Основные показатели:

Пример расчета поддержки S для правила салат→помидоры

Пример расчета достоверности С для правила салат→помидоры

Проверка зависимости А от B в правиле A→B
S(А,B) ≈ S(A)·S(B)
Если выполняется, то A и B
независимы друг от друга и правило A→B непригодно.
Пример:
Всего транзакций 100 штук.
А и В встречаются совместно в 50 транзакциях: S(А,B)=50/100
А встречается в 70 транзакциях: S(A)=70/100
B встречается в 80 транзакциях: S(B)=80/100
Проверим по правилу выше:
S(А,B) ≈ S(A)·S(B)
0,5 ≈ 0,7·0,8
0,5 ≈ 0,56. Наше правило выполняется, это значит, что условие A и следствие B часто встречаются вместе, не менее часто они встречаются и по отдельности. Правило A→B непригодно.

Лифт, L для правила A→B – это отношение
С(A→B)
S(B)
Значения лифта большие, чем единица, показывают, что условие чаще появляется в транзакциях, содержащих следствие, чем в остальных. Можно сказать, что лифт является обобщенной мерой связи двух предметных наборов: при значениях лифта > 1 связь положительная, при 1 она отсутствует, а при значениях < 1 — отрицательная.

Рассмотрим пример использования лифта для меры связи в двух правилах:
1. Помидоры →салат
2. Помидоры → конфеты

S(салат) = 4/10 = 0,4; С(помидоры → салат) = 4/7 = 0,57.
Следовательно, L(помидоры → салат) = 0,57/0,4 = 1,425. >1, хорошо

S(конфеты) = 6/10; С(помидоры → конфеты) = 4/7 =0,57.
Тогда L(помидоры → конфеты) = 0,57/0,6 = 0,95. <1 плохо

Противоречие использование меры лифт
Хотя лифт используется широко, он не всегда оказывается удачной мерой значимости правила. Правило с меньшей поддержкой и большим лифтом может быть менее значимым, чем альтернативное правило с большей поддержкой и меньшим лифтом, потому что последнее применяется для большего числа покупателей. Значит, увеличение числа покупателей приводит к возрастанию связи между условием и следствием.

Мера левередж, Т для правила A→B – это разность
Левередж применяется для сравнения значимости двух и более правил, у которых поддержка и достоверность одинаковые.
Чем левередж больше, тем значимее правило.

Сравним значимость двух правил:
морковь → помидоры
салат → помидоры
И определим, какое из правил значимее (“сильней”)

С(морковь → помидоры) = 3 / 3 = 1 L(…)=1/S(помидоры)=1/(6/10)
С(салат → помидоры) =3 / 3 = 1 L(…)=1/S(помидоры)=1/(6/10)