Аксиомы стереометрии

Повторить аксиомы планиметрии
Познакомиться с аксиомами стереометрии
Уметь соотносить математическую формулировку аксиомы с графическим изображением
Уметь формулировать ответы, используя строгость математического языка
Продолжать учиться работать в группах
Совершенствовать навыки работы с тестами
Цели урока

Что изучает планиметрия?
Как обозначают прямые и точки на плоскости?
Какие аксиомы планиметрии вы помните?
Планиметрия

Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
A
B
Аксиома №1

Через любые две точки можно провести прямую и только одну.
Аксиома №2
а

Из трех точек только одна лежит между двумя другими.
Аксиома №3
а

Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Аксиома №4

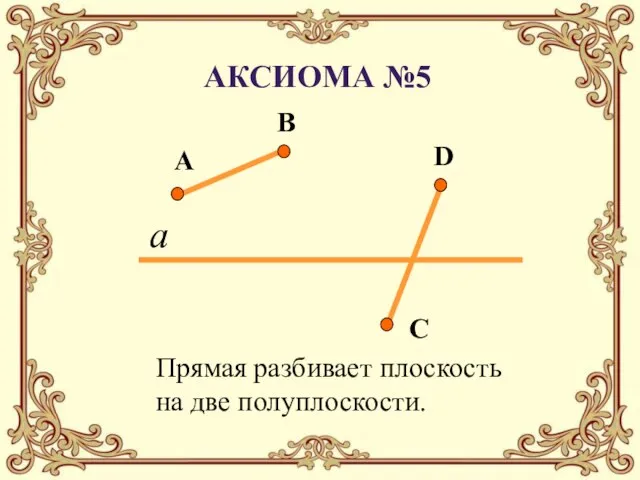
Прямая разбивает плоскость на две полуплоскости.
Аксиома №5

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180º. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Аксиома №6

На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и только один.
Аксиома №7
а

На любой полупрямой от начальной точки можно отложить угол с заданной градусной меры, меньшей 180º и только один.
Аксиома №8

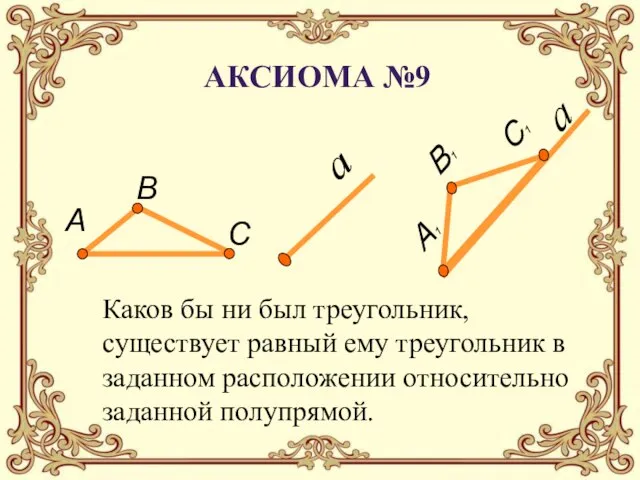
Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно заданной полупрямой.
Аксиома №9

Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Аксиома №10

Что изучает стереометрия?
Основные фигуры в пространстве?
Плоскость на рисунке
изображается в виде…?
Приведите примеры моделей плоскостей, окружающих нас.
Стереометрия

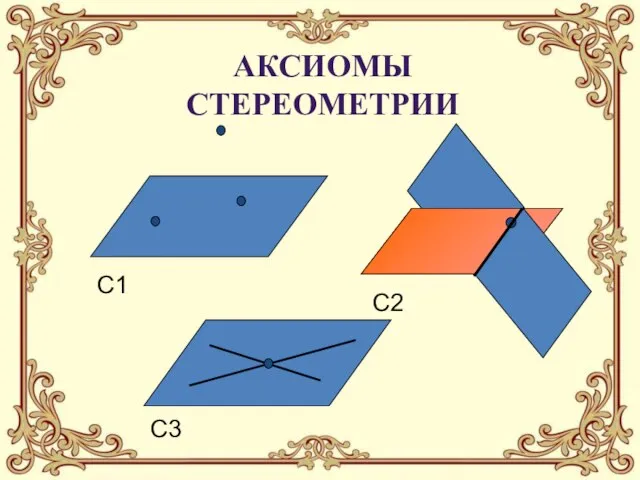
C1
C2
C3
Аксиомы стереометрии

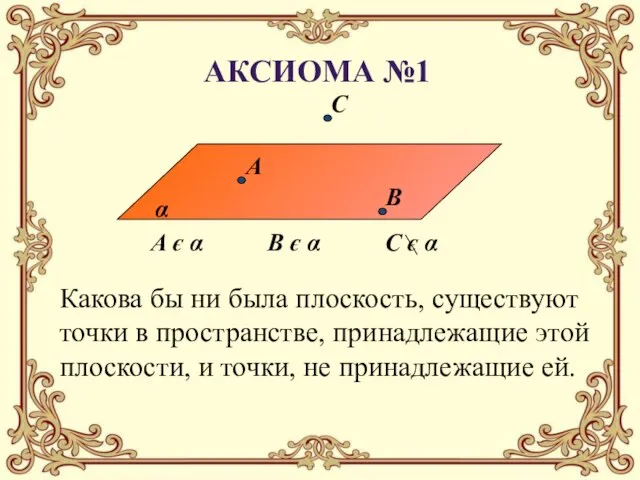
А є α
В є α
Аксиома №1
Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.

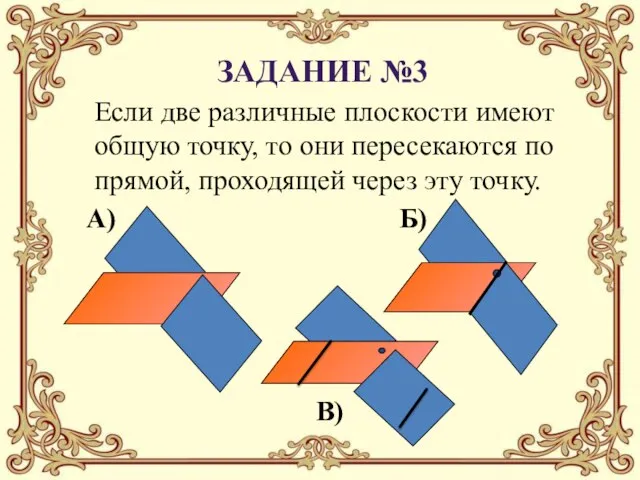
Аксиома №2
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
А

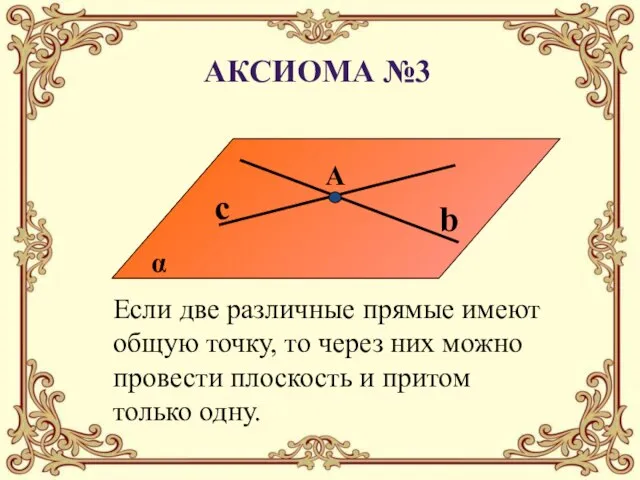
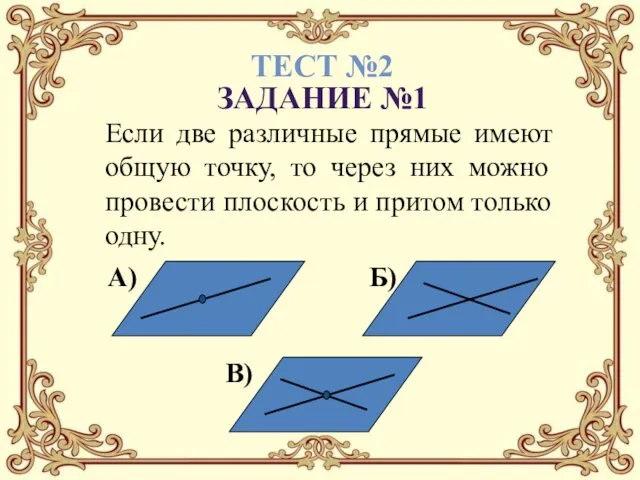
Аксиома №3
Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.

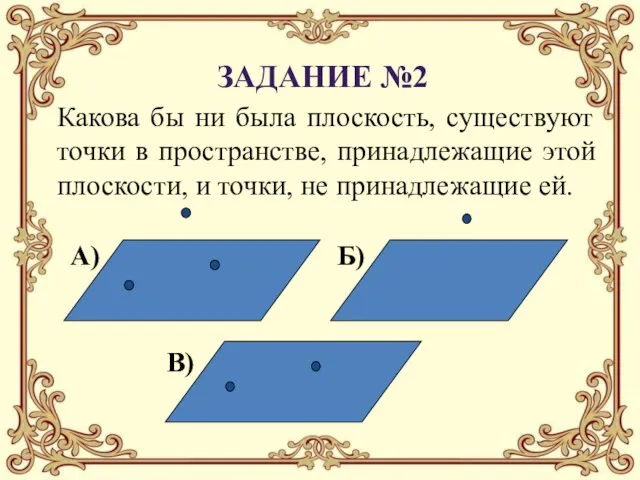
А) Как бы ни было, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Б) Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.
В) Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости.
Г) Какова бы ни была плоскость, существуют точки в пространстве, не принадлежащие ей.
Задание №1
ТЕСТ №1

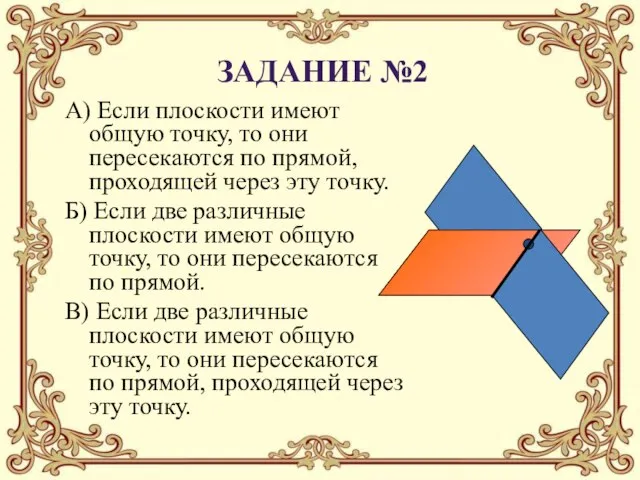
А) Если плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Б) Если две различные плоскости имеют общую точку, то они пересекаются по прямой.
В) Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Задание №2

А) Через две прямые можно провести плоскость и притом только одну.
Б) Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.
В) Если прямые имеют общую точку, то через них можно провести плоскость.
Задание №3

1 – Б) Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.
2 – В) Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
3 – Б) Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.
ПРОВЕРЬ СЕБЯ
Ответы на Тест №1

Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.
Задание №1
ТЕСТ №2

Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.
В)
Б)
А)
Задание №2

Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Задание №3

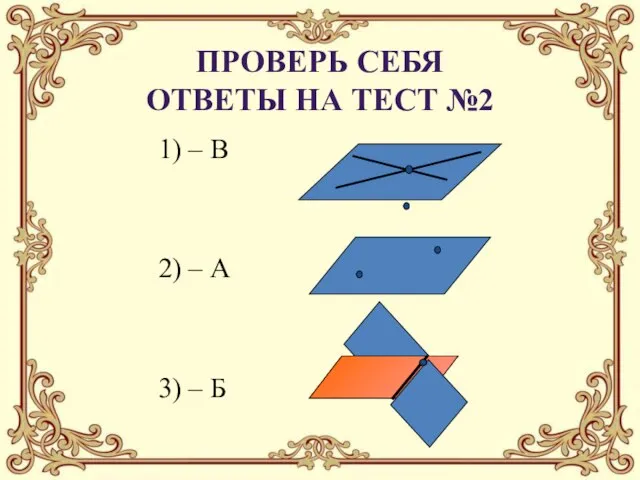
1) – В
2) – А
3) – Б
ПРОВЕРЬ СЕБЯ
Ответы на Тест №2

Группа 1, 4 – задача №1
Группа 2, 5 – задача №2
Группа 3, 6 – задача №3
Практическая работа
(Для самопроверки)

Из задач №1-4 (две обязательные для решения)
Третья задача по выбору
Составить задачу на применение аксиом (по желанию).
Домашнее задание

Итог урока