Содержание
- 2. «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего
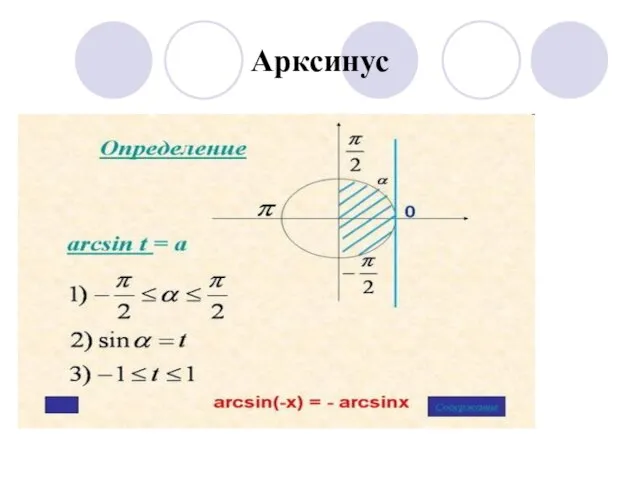
- 3. Арксинус
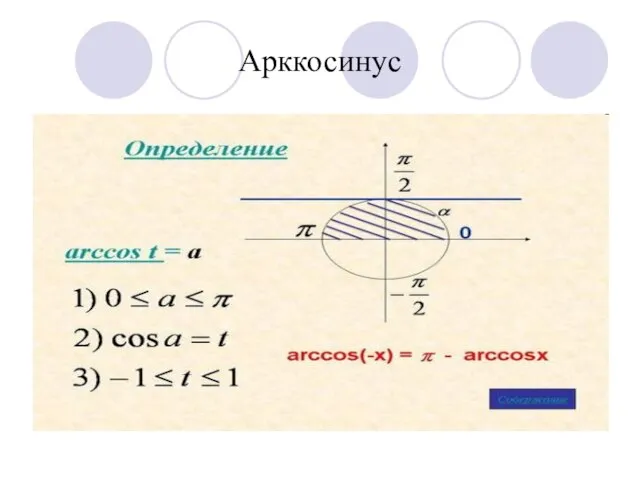
- 4. Арккосинус
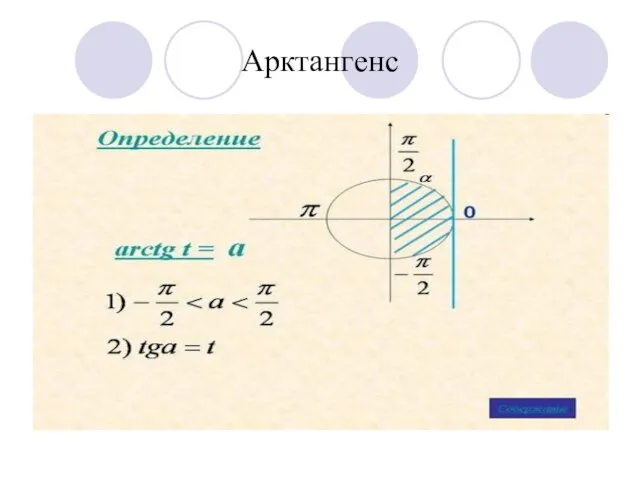
- 5. Арктангенс
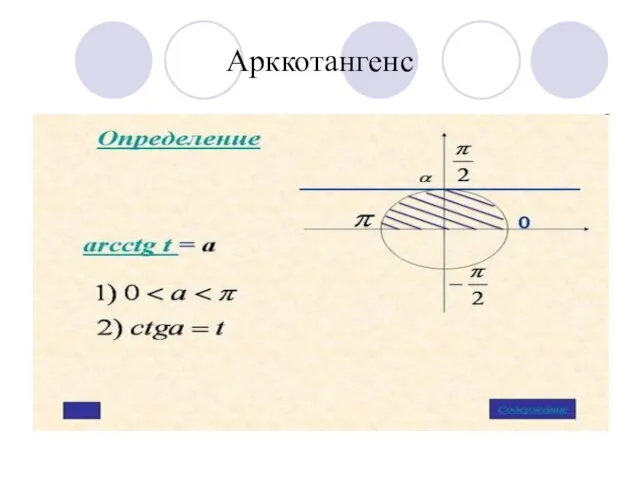
- 6. Арккотангенс
- 7. Финк- Райт – Раунд - Робин arcsin √2/2 arccos 1 arcsin (- 1/2 ) arccos (-
- 8. Ответы π/4 0 - π/6 5π/6 π/3
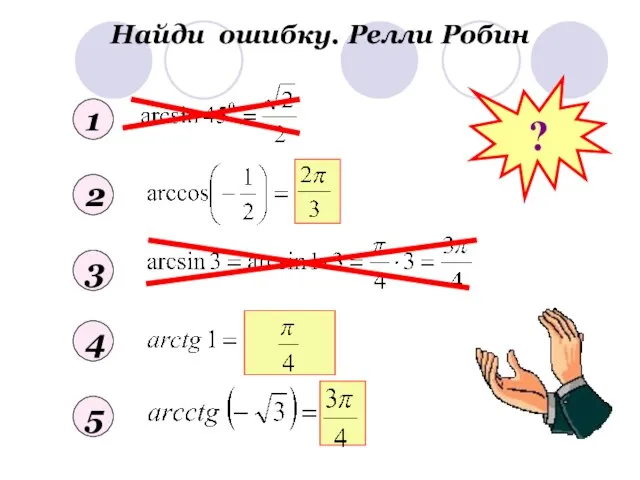
- 9. Найди ошибку. Релли Робин 1 2 3 4 5 ?
- 10. Оценка
- 11. Общая схема исследования функции 1. Область определения функции. 2. Исследование области значений функции 3. Исследование функции
- 12. Функция у = sin x. 1. Областью определения функции является множество всех действительных чисел ( R
- 13. Функция у = соs x. 1. Областью определения функции является множество всех действительных чисел ( R
- 14. Функция у = tg x 1. Областью определения функции является множество (- π/2; π/2) 2. Областью
- 15. Функция у = ctg x 1. Областью определения функции является множество (πn; π + πn) 2.
- 16. Клок Бадис Пример 1Пример 1. sin x = − Пример 2Пример 2. cos x = Пример
- 17. Пример 1 sin x = −
- 18. Пример 2 cos x =
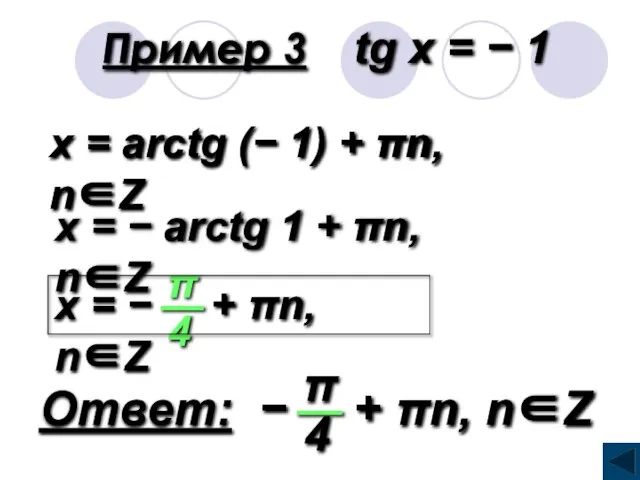
- 19. Пример 3 tg x = − 1 x = arctg (− 1) + πn, n∈Z x
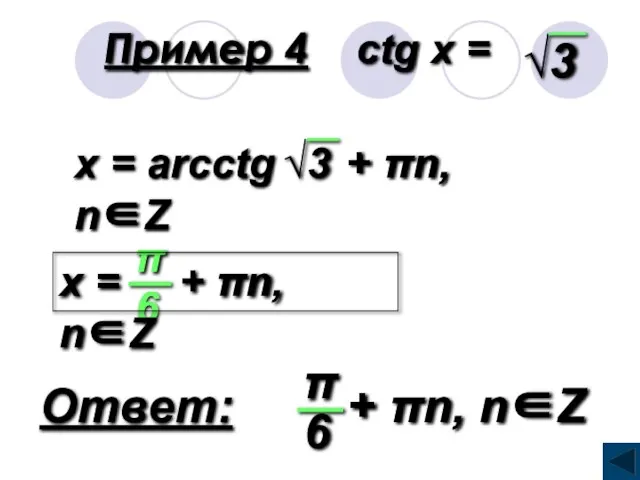
- 20. Пример 4 сtg x =
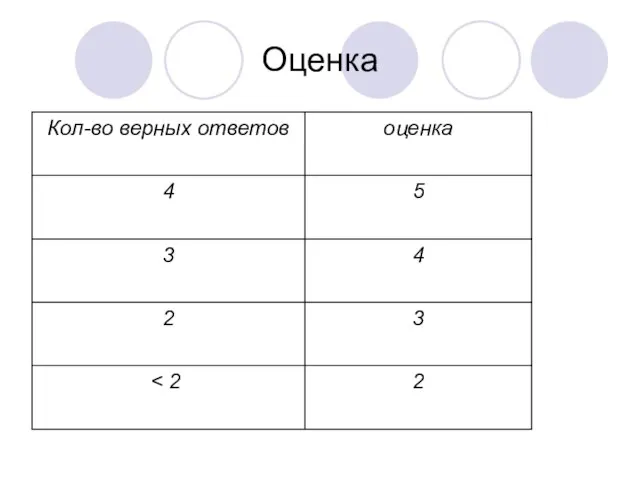
- 21. Оценка
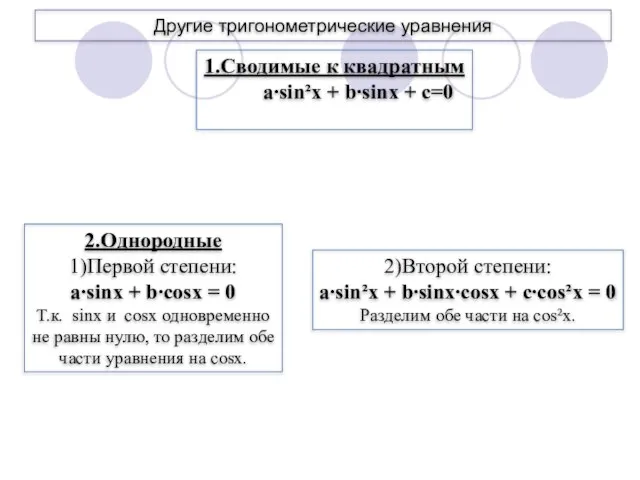
- 22. Другие тригонометрические уравнения 1.Сводимые к квадратным a∙sin²x + b∙sinx + c=0 2.Однородные 1)Первой степени: a∙sinx +
- 23. Содержание Метод замены переменной Метод разложения на множители С помощью тригонометрических формул: Формул сложения Формул приведения
- 24. Основные методы решения тригонометрических уравнений. Домашнее задание. На «3» 1) 3 sin x+ 5 cos x
- 25. « То, что мы знаем, - ограниченно, а то чего мы не знаем, - бесконечно». Пьер
- 26. Спасибо!
- 28. Скачать презентацию








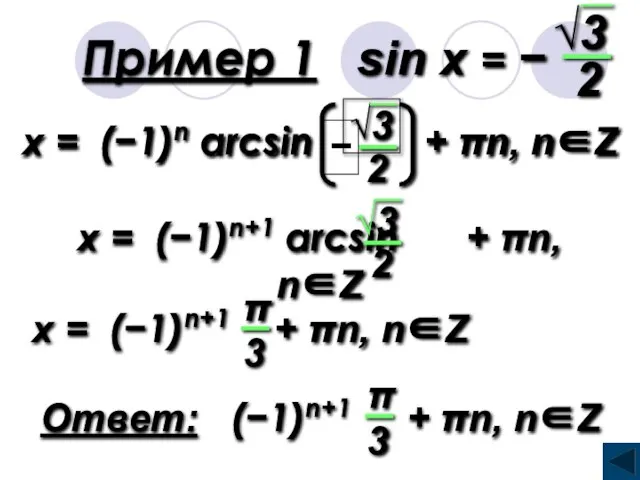





 Предквантум
Предквантум Старинные зимние обычаи и праздники, «Рождество», «Святки»
Старинные зимние обычаи и праздники, «Рождество», «Святки» ВИДЕО-СТЕНА DIBOSS LB-40
ВИДЕО-СТЕНА DIBOSS LB-40 Новый подход к интеграции календарно-сетевых графиков и смет
Новый подход к интеграции календарно-сетевых графиков и смет Областной конкурс Методическая разработка дистанционного урока - 2021
Областной конкурс Методическая разработка дистанционного урока - 2021 Музей путешествий. Поклонная гора. Парк Победы
Музей путешествий. Поклонная гора. Парк Победы Товары и услуги
Товары и услуги Техническое регулирование
Техническое регулирование 20140305_lekarstvennye_rasteniya_buturlinovskogo_rayona
20140305_lekarstvennye_rasteniya_buturlinovskogo_rayona Консолидация ритейла в Украине: роль логистики 1.Предпосылки для консолидации ритейла 2.Когда ритейлеру нужен 3PL-оператор? 3.Case study 4.
Консолидация ритейла в Украине: роль логистики 1.Предпосылки для консолидации ритейла 2.Когда ритейлеру нужен 3PL-оператор? 3.Case study 4. Project on the Indian Ocean
Project on the Indian Ocean  Портретная студийная съёмка
Портретная студийная съёмка Внешняя политика Советского государства 1920-х
Внешняя политика Советского государства 1920-х СТРОКА, ОБОРВАННАЯ ПУЛЕЙ
СТРОКА, ОБОРВАННАЯ ПУЛЕЙ ЕГЭ В 3 «Площади»
ЕГЭ В 3 «Площади» Цветовой контраст (хроматический)
Цветовой контраст (хроматический) Фотожурналист Владимир Вяткин
Фотожурналист Владимир Вяткин 26-27 апреля 2006 года Центр практической психологии РГУ имени С.А. Есенина Московский городской психолого-педагогический университе
26-27 апреля 2006 года Центр практической психологии РГУ имени С.А. Есенина Московский городской психолого-педагогический университе Кейс-стади для педагогов
Кейс-стади для педагогов Об аксиомах геометрии
Об аксиомах геометрии Презентация на тему Родная природа в стихотворениях поэтов xx века
Презентация на тему Родная природа в стихотворениях поэтов xx века  Каталог Атоми
Каталог Атоми Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по русскому языку Соловьева Т.В., предсе
Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по русскому языку Соловьева Т.В., предсе Создание новогодней открытки на основе пейзажа «Зимние россыпи»
Создание новогодней открытки на основе пейзажа «Зимние россыпи» Внесем порядок в хаос! ИЗО 7 класс
Внесем порядок в хаос! ИЗО 7 класс Космонавты, рожденные Украиной: космонавты Луганщины
Космонавты, рожденные Украиной: космонавты Луганщины Межрегиональный образовательный форум «Открытое образовательное пространство: живая праКтика тьюторства»
Межрегиональный образовательный форум «Открытое образовательное пространство: живая праКтика тьюторства» ДДК. Экскурсия
ДДК. Экскурсия