Множества

Понятие множества.
Георг Кантор (1845-1918)
Профессор математики и философии, основоположник современной теории множеств.
«Под множеством мы подразумеваем объединение в целое определённых, различающихся между собой объектов нашего представления или мышления». Георг Кантор

Понятие множества.
Основное понятие в математике - понятие множества.
Понятие множество относится к первоначальным понятиям, не подлежащим определению.
Под множеством подразумевается некоторая совокупность однородных объектов.
Предметы ( объекты), составляющие множество, называются элементами.

Обозначение множества
Множества обозначаются заглавными буквами латинского алфавита: A, B, C, X и др.
Элементы множества обозначаются строчными буквами латинского алфавита : a, b, c, d и др.
Запись M = { a , b, c, d } означает, что множество М состоит из элементов a , b, c, d.
Є – знак принадлежности. Запись а є М обозначает, что объект а является элементом множества М и читается так:
« а принадлежит множеству М »

Численность множества
Численность множества- число элементов в данном множестве.
Обозначается так : n
Записывается так : n (М) = 4
Множества бывают:
Конечные множества- состоят из конечного числа элементов, когда можно пересчитать все элементы множества.
Бесконечные множества- когда невозможно пересчитать все элементы множества.
Пустые множества- множества, не содержащие элементов и обозначают так: Ø . Записывают так: n (A)=0 ; A= Ø
Пустое множество является подмножеством любого множества.

Виды множеств:
Дискретные множества(прерывные)- имеют отдельные элементы. Путём счёта распознаются.
Непрерывные множества- нет отдельных элементов. Распознаются путём измерения.
Конечные множества- состоят из конечного числа элементов, когда можно пересчитать все элементы множества.
Бесконечные множества- когда невозможно пересчитать все элементы множества.
Упорядочные множества. Элемент из множества предшествует или следует за другим. Множество натуральных чисел, расположенных в виде натурального ряда.
Неупорядочные множества. Любое неупорядочное множество можно упорядочить.

Способы задания множеств
Перечислением элементов (подходит для конечных множеств).
Указать характеристическое свойство множества, т.е. то свойство, которым обладают все элементы данного множества.
С помощью изображения :
На луче
В виде графика
С помощью кругов Эйлера. В основном используется при выполнении действий с множествами или демонстрации их отношений.

Подмножество
Если любой элемент множества В принадлежит множеству А,
то множество В называется подмножеством множества А.
- Знак включения.
Запись В А означает,
что множество В является подмножеством множества А.

Виды подмножеств
Собственное подмножество. Множество В называется собственным подмножеством множества А, если выполняются условия: В≠Ø, В≠А.
Не собственные подмножества. Множество В называется не собственным подмножеством множества А, если выполняются условия: В≠Ø, В=А.
Пустое множество является подмножеством любого множества.
Любое множество является подмножеством самого себя.

А
В
А=В
Равенства множеств
Множества равны, если они состоят из одних и тех же элементов.
Два множества являются равными , если каждый из них является подмножеством другого.
В этом случае пишут: А=В

Операции над множествами
Пересечение множеств.
Объединение множеств.
Разность множеств.
Дополнение множества.

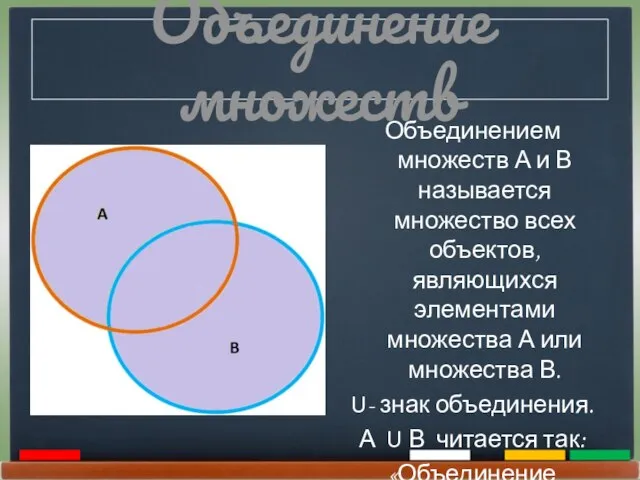
Объединение множеств
Объединением множеств А и В называется множество всех объектов, являющихся элементами множества А или множества В.
U- знак объединения.
А U В читается так:
«Объединение множества А и множества В».

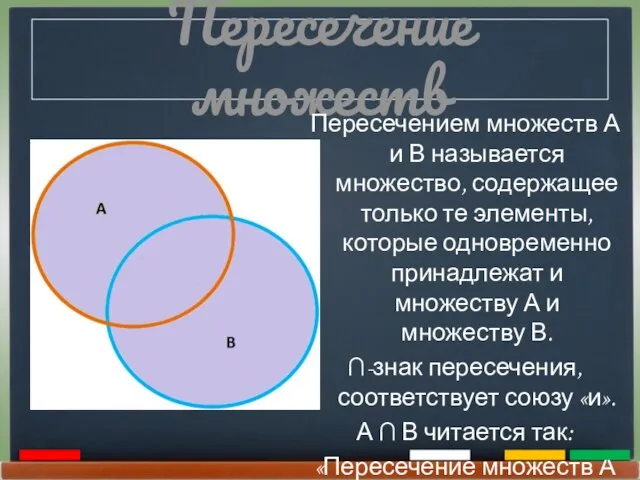
Пересечение множеств
Пересечением множеств А и В называется множество, содержащее только те элементы, которые одновременно принадлежат и множеству А и множеству В.
∩-знак пересечения, соответствует союзу «и».
А ∩ В читается так:
«Пересечение множеств А и В»

Разность множеств
Разностью множеств А и В называется множество всех объектов, являющихся элементами множества А и не принадлежащих множеству В.
\ - знак разности, соответствует предлогу «без».
Разность множеств А и В записывается так: А \ В

Дополнение множества
Множество элементов множества В, не принадлежащих множеству А, называется дополнением множества А до множества В.
Часто множества являются подмножествами некоторого основного, или универсального множества U.
Дополнение обозначается Ā

Свойства множеств
Пересечение и объединение множеств обладают свойствами:
Коммутативность
Ассоциативность
Дистрибутивность

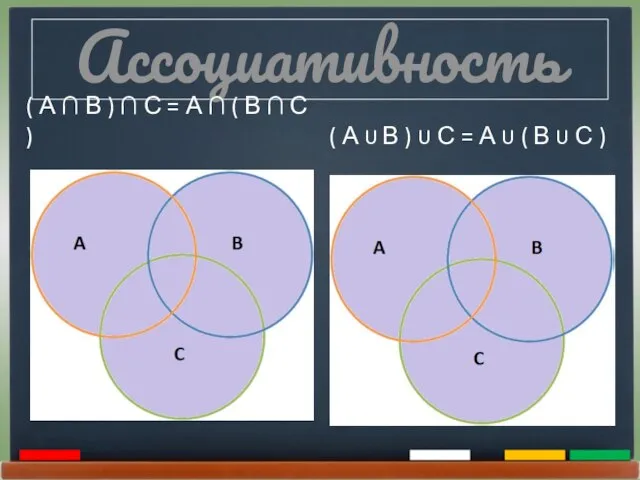
Ассоциативность
( А ∩ В ) ∩ С = А ∩ ( В ∩ С )
( А U В ) U С = А U ( В U С )

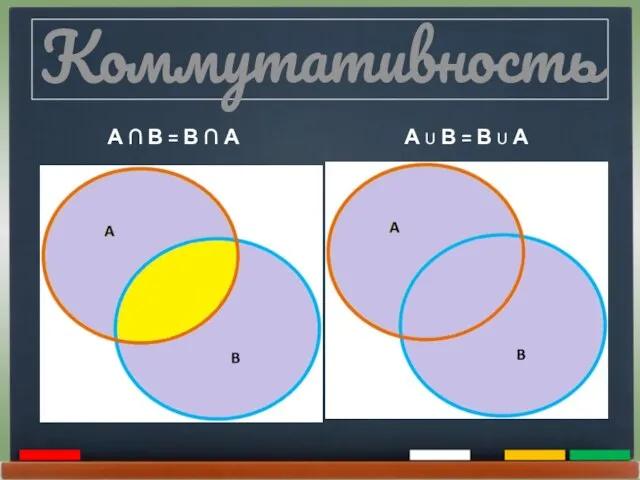
Коммутативность
А ∩ В = В ∩ А
А U В = В U А

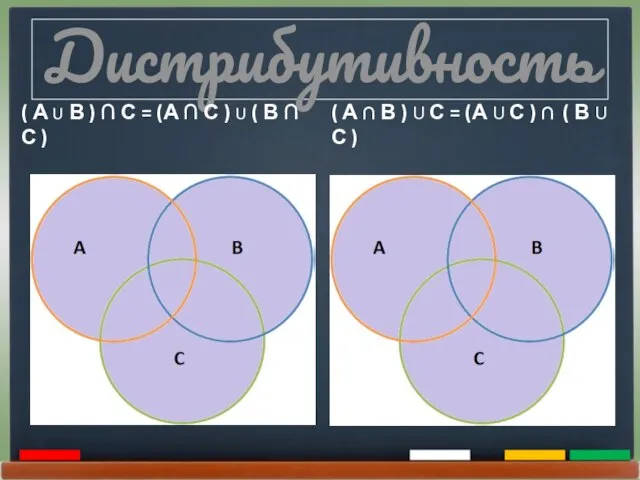
Дистрибутивность
( А U В ) ∩ С = (А ∩ С ) U ( В ∩ С )
( А ∩ В ) U С = (А U С ) ∩ ( В U С )

Отношения множеств
В теории множеств рассматриваются отношения между множествами:
Тождественность. Если каждый элемент множества А является также и элементом множества В , и каждый элемент множества В есть также элементом множества А, то эти множества тождественны. Обозначается так : А=В.
Эквивалентность. Соответствие между элементами множеств А и В, при котором каждому элементу множества А соответствует единственный элемент множества В, и наоборот, различным элементам одного множества соответствуют различные элементы другого множества, называется взаимно однозначными. Если существует, по крайней мере, одно взаимно однозначное соответствие между элементами множеств А и В, то такие множества называются эквивалентными.