Алгебра логики

Логика
Логика – это наука о формах и законах человеческой мысли, о законах доказательных рассуждений, изучающая методы доказательств и опровержений, т.е. методы установления истинности или ложности одних высказываний (утверждений) на основе истинности или ложности других высказываний.

Алгебра логики
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний.

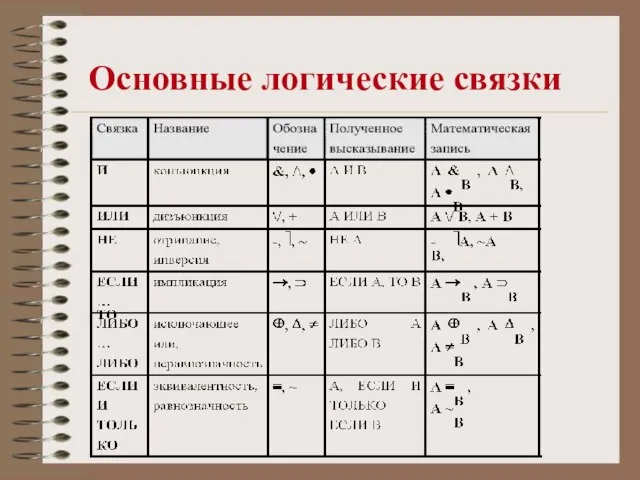
Основные логические связки

Таблица истинности
Таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Таблица истинности
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0,0), (0,1), (1,0), (1,1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0,0,0), (0,0,1), (0,1,0), (0,1,1),
(1,0,0), (1,0,1), (1,1,0), (1,1,1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.

Основные логические операции
КОНЪЮНКЦИЯ
Соответствует союзу И;
Обозначение &;
В языках программирования and;
Название: Логическое умножение.

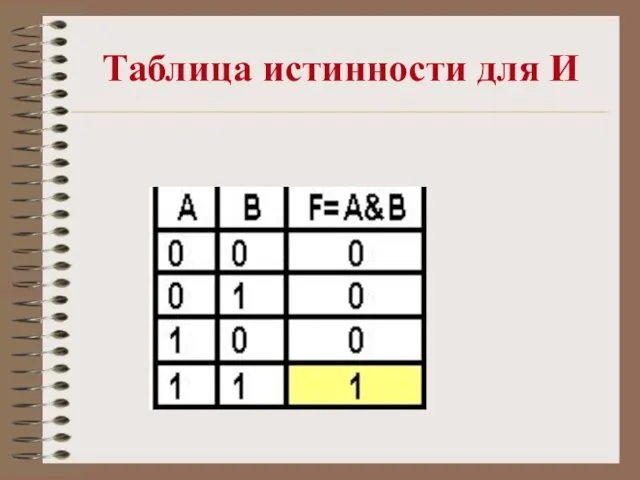
Таблица истинности для И

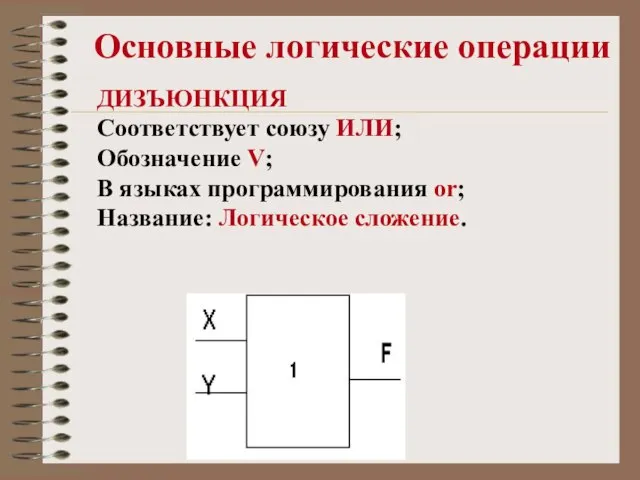
Основные логические операции
ДИЗЪЮНКЦИЯ
Соответствует союзу ИЛИ;
Обозначение V;
В языках программирования or;
Название: Логическое сложение.

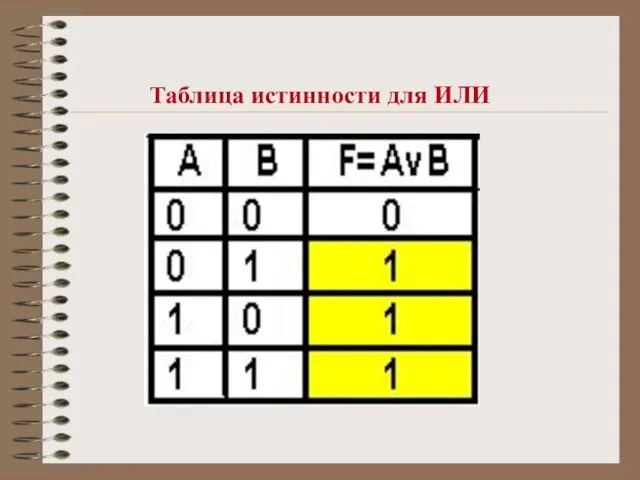
Таблица истинности для ИЛИ

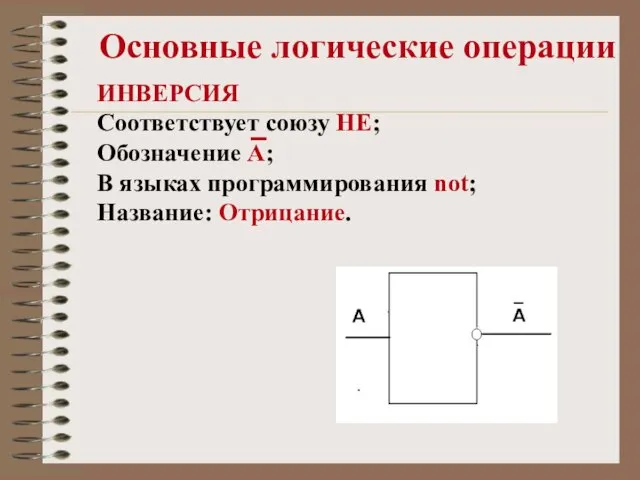
Основные логические операции
ИНВЕРСИЯ
Соответствует союзу НЕ;
Обозначение А;
В языках программирования not;
Название: Отрицание.

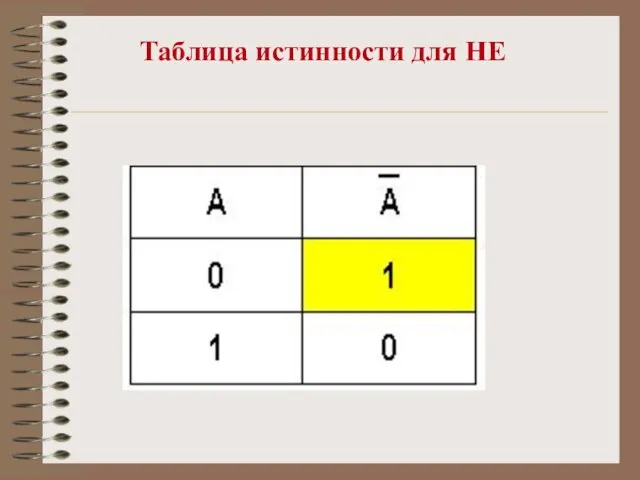
Таблица истинности для НЕ

Таблица истинности для
эквивалентности

Порядок выполнения логических операций
Порядок выполнения логических операций задается круглыми скобками.
Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация →.

Логическая формула
Определение логической формулы:
Всякая логическая переменная и символы “истина” (“1”) и “ложь” (“0”) — формулы.
Если А и В — формулы, то , (А • В),
(А v В), (А → B), (А ↔ В) — формулы.

Тавтология
Некоторые формулы принимают значение “истина” при любых значениях истинности входящих в них переменных. Например, формула А v
Такие формулы называются тождественно истинными формулами или тавтологиями.
Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.

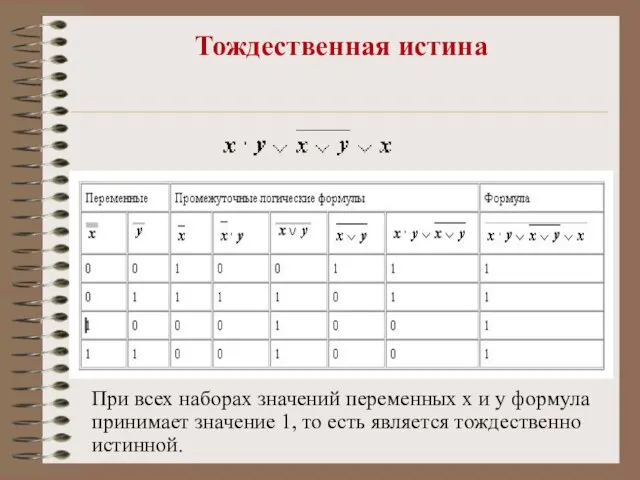
Тождественная истина
При всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.

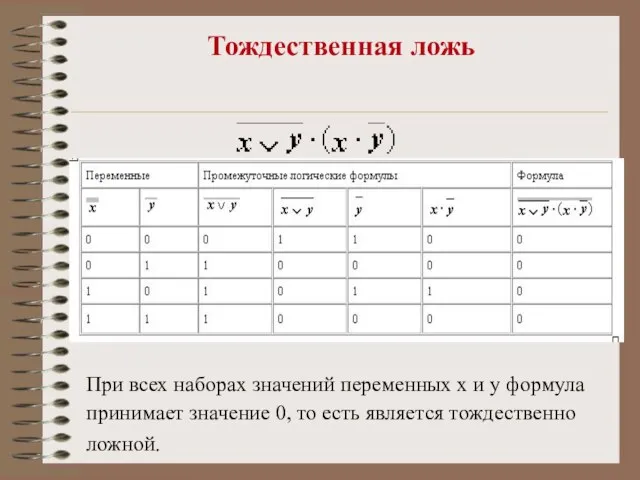
Тождественная ложь
В качестве другого примера рассмотрим формулу А • , которой соответствует, например, высказывание “Катя самая высокая девочка в классе, и в классе есть девочки выше Кати”. Очевидно, что эта формула ложна, так как либо А, либо обязательно ложно.
Такие формулы называются тождественно ложными формулами или противоречиями.
Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.

Тождественная ложь
При всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.

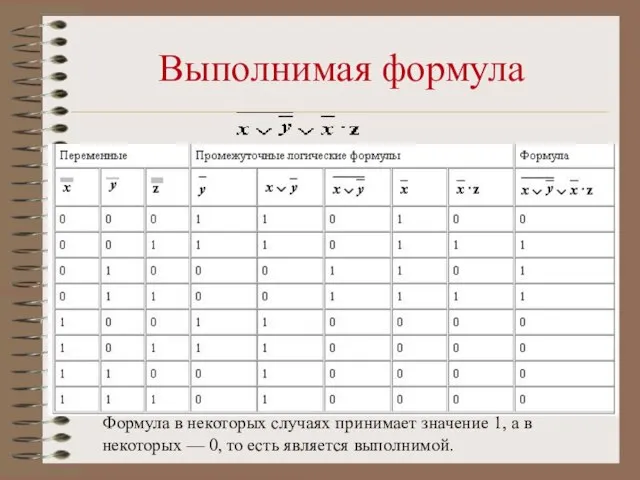
Выполнимая формула
Формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.