Содержание
- 2. СОДЕРЖАНИЕ Введение. Логическая операция конъюнкция. Логическая операция дизъюнкция. Логическая операция инверсия. Логическая операция импликация. Логическая операция
- 3. АЛГЕБРА в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые
- 4. Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт – истинно или ложно
- 5. Простые высказывания в алгебре логики обозначаются заглавными буквами А = {Аристотель – основоположник логики} В =
- 6. Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические
- 7. Логическая операция КОНЪЮНКЦИЯ (логическое умножение) В естественном языке соответствует союзу и В алгебре высказываний обозначается ⋅
- 8. Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным
- 9. Пример. Даны высказывания. Определите истинность каждого из них. А = {10 делится на 2 и 5
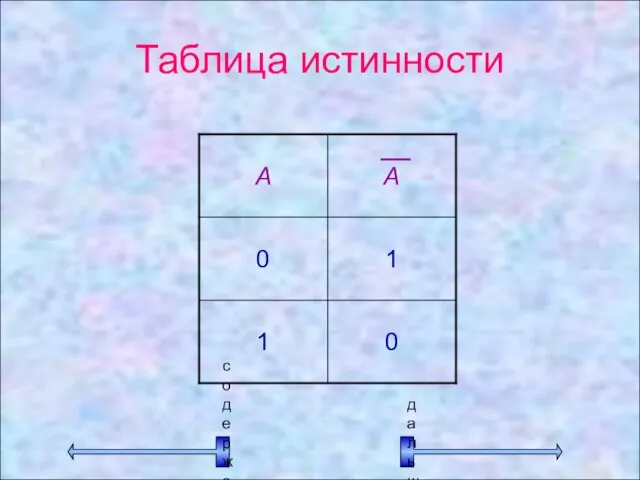
- 10. Таблица истинности содержание дальше
- 11. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение) В естественном языке соответствует союзу или. В алгебре высказываний обозначается ∨
- 12. Дизъюнкция – Дизъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание,
- 13. Пример. Даны высказывания. Определите истинность каждого из них. Пример. Даны высказывания. Определите истинность каждого из них.
- 14. Таблица истинности Таблица истинности содержание дальше
- 15. Логическая операция ОТРИЦАНИЕ (инверсия) В естественном языке соответствует частице не. В алгебре высказываний обозначается А, ¬А
- 16. Отрицание – это логическая операция, которая каждому простому истинному высказыванию ставит в соответствие ложное высказывание.
- 17. Пример А = {Луна – спутник Земли} А = {Луна – не спутник Земли}
- 18. Таблица истинности содержание дальше
- 19. Логическая операция ИМПЛИКАЦИЯ (логическое следование) Логическая операция ИМПЛИКАЦИЯ (логическое следование) В естественном языке соответствует обороту если
- 20. Импликация – Импликация – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание,
- 21. Пример. Даны высказывания. Пример. Даны высказывания. А = {Данный четырехугольник - квадрат} В = {Около данного
- 22. А истинно и В истинно, т. е. если данный четырехугольник – квадрат, то около него можно
- 23. В обычной речи связка «если …, то» описывает причинно-следственную связь между высказываниями. Но в логических операциях
- 24. Таблица истинности Таблица истинности дальше содержание
- 25. Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность) Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность) В естественном языке соответствует оборотам речи тогда и
- 26. Эквиваленция – Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание,
- 27. Пример. Определить истинность высказываний. Пример. Определить истинность высказываний. А = {24 делится на 6 тогда и
- 28. Таблица истинности Таблица истинности содержание дальше
- 29. спасибо за внимание и активную работу!
- 31. Скачать презентацию



























 КОНКУРС по информационно-коммуникационным технологиям Проект: «Покрышкин А.И. –трижды Герой Советского Союза» Авт
КОНКУРС по информационно-коммуникационным технологиям Проект: «Покрышкин А.И. –трижды Герой Советского Союза» Авт And also in the retail business
And also in the retail business Порядок создания предприятия
Порядок создания предприятия Федорко Надежда Никифоровна
Федорко Надежда Никифоровна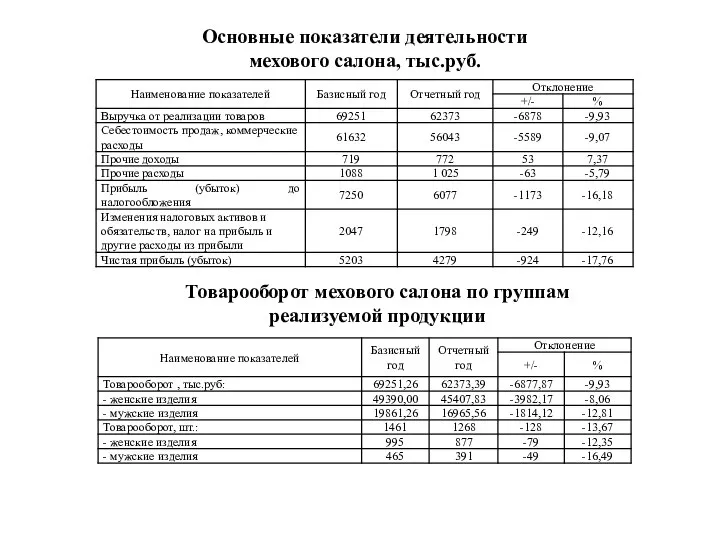 Товарооборот мехового салона по видам товарных групп
Товарооборот мехового салона по видам товарных групп ПРОВОДЯЩИЕ ПОЛИМЕРЫ
ПРОВОДЯЩИЕ ПОЛИМЕРЫ Дискуссия
Дискуссия Морская транспортная система
Морская транспортная система СПЕЦИАЛЬНОСТЬ«СТРАХОВОЕ ДЕЛО»
СПЕЦИАЛЬНОСТЬ«СТРАХОВОЕ ДЕЛО» Famous Psychologists Alfred Adler
Famous Psychologists Alfred Adler Аэромеханика
Аэромеханика Создание продукта
Создание продукта  The Incredible Sun
The Incredible Sun  Откуда взять клиентов? Эффективные инструменты привлечения и удержания клиентов в интернете Анна Банникова
Откуда взять клиентов? Эффективные инструменты привлечения и удержания клиентов в интернете Анна Банникова Класс Птицы 1 класс
Класс Птицы 1 класс Презентация на тему Различение частиц НЕ и НИ
Презентация на тему Различение частиц НЕ и НИ Ворлд Скилс. История
Ворлд Скилс. История «Вегетативное размножение махровой глоксинии листовыми черенками»
«Вегетативное размножение махровой глоксинии листовыми черенками» Феодальная раздробленность на Руси
Феодальная раздробленность на Руси Презентация на тему: Понятие квадратного корня из неотрицательного числа
Презентация на тему: Понятие квадратного корня из неотрицательного числа MY SPORT IDOL IS SVETLANA KHORKINA
MY SPORT IDOL IS SVETLANA KHORKINA  За 5 минут вендинговый автомат способен продать 25 единиц Товара. 5 минут – достаточно, чтобы проверить, какой Доход принес Ваш Биз
За 5 минут вендинговый автомат способен продать 25 единиц Товара. 5 минут – достаточно, чтобы проверить, какой Доход принес Ваш Биз Построение графика функции с помощью производной.
Построение графика функции с помощью производной. РЕАЛЬНІ ГАЗИ
РЕАЛЬНІ ГАЗИ  Презентация на тему Компьютерные сети Классификация
Презентация на тему Компьютерные сети Классификация  Сжатие данных
Сжатие данных Расшифровка сокращений в детализации и Мобильной детализации
Расшифровка сокращений в детализации и Мобильной детализации Что такое Андертейл
Что такое Андертейл