Логически основи в компютъра

Логическите основи на компютъра използват формален апарат, който се нарича математическа логика, логическа алгебра или булева алгебра.

Мнозина учени са дали своя принос за развитието на тази част от математиката, но сме длъжни да споменем ирландския математик Джордж Бул (1815 - 1864), който полага основите на математическата логика (неслучайно се среща и терминът Булева алгебра).

1. Съждение
А) Определение
Б) Видове съждения

А) Определение
Всяка мисъл или изречение, за което може да се каже дали то е вярно т.е. истина или не е вярно т.е. неистина.
Примери
Днес е слънчево.
Аз обичам информатиката, но нямам компютър.

Ако едно съждение е вярно, казваме че то има верностна стойност истина, а ако не е вярно, казваме че верностната му стойност е неистина (лъжа).

За означаване на стойността истина се използва Т (true - истина(англ.)) или 1, а за означаване на стойността неистина се използва F (false - лъжа(англ.)) или 0.

Тъй като всяко съждение може да има верностна стойност истина или неистина (1 или 0), то наричаме логиката двузначна или още двоична.

Стойностите 1(Т) и 0(F) се наричат съждителни константи, а променливите, които приемат само такива стойности,се наричат съждителни променливи (означават се с буквите от латинската азбука).

Б) Видове съждения
Прости – Съждения, които не съдържат в себе си други съждения, се наричат прости.
Пр. Иван е чернокос.
Сложни – Сложни или съставни се наричат такива съждения, които се състоят от поне две прости съждения.
Пр. Тони също е чернокос, но сега се е изрусил.

2. Образуване на сложни съждения
А) Отношение “И”
Б) Отношение “ИЛИ”
В) Отношение “НЕ”

А) Отношение “И”
Вярно е когато свързаните чрез него съждения са едновременно верни
Пример 1
Стоян е отличник по информатика, но няма компютър.

1) Стоян е отличник – истина
И
Стоян няма компютър – истина
Следователно съждението е вярно и има верностна стойност 1.

2) Стоян е отличник – истина
И
Стоян няма компютър – неистина
Следователно съждението е невярно и има верностна стойност 0.

3) Стоян е отличник – неистина
И
Стоян няма компютър – истина
Следователно съждението е невярно и има верностна стойност 0.

4) Стоян е отличник – неистина
И
Стоян няма компютър – неистина
Следователно съждението е невярно и има верностна стойност 0.

Б) Отношение “ИЛИ”
Вярно е когато поне едно от двете свързани чрез него съждения е вярно.
Примери
Ромбът не е квадрат или трапецът е успоредник.
Ромбът е квадрат или трапецът е успоредник.
Робът е квадрат или трапецът е правоъгълник.

Ромбът не е квадрат – истина
или
трапецът е успоредник – истина
Следователно съждението е вярно и има верностна стойност 1.

Ромбът е квадрат – неистина
или
трапецът е успоредник – истина
Следователно съждението е вярно и има верностна стойност 1.

Ромбът е квадрат – неистина
или
трапецът е правоъгълник – неистина
Следователно съждението е невярно и има верностна стойност 0.

В) Отношение “НЕ”
За всяко съждение може да се образува неговото отрицание. Ако даденото съждение е истина, то неговото отрицание не е и обратното.
Примери
Информатиката е любимият ми предмет.
Математиката не е любимият ми предмет.

Информатиката е любимият ми предмет.
Отрицанието:
Информатиката НЕ е любимият ми предмет.

Математиката не е любимият ми предмет.
Отрицанието:
Математиката е любимият ми предмет.

3. Логически променливи и функции
А) Конюнкция
Б) Дизюнкция
В) Инверсия
Г) Импликация
Д) Изключваща дизюнкция
Е) Равнозначност

Начините по които човек може да свързва простите съждения в сложни, както и необходимостта от това да знае как да определи верностната стойност на едно сложно съждение, ако знае стойностите на съставящите го прости, водят до изучаване и класифициране на логическите функции.

А) Конюнкция
логическо умножение ,,И" - конюнкция - има два аргумента и има стойност 0, когато поне един от аргументите й има стойност 0, и 1, когато и двата аргумента са равни на 1.
Означава се с ^ или с AND, например aANDb или a^b.
Таблица за истинност:

Б) Дизнюнкция
Логическо събиране ,,ИЛИ" - дизюнкция - има два аргумента и има стойност 1, когато поне един от аргументите й има стойност 1, и 0, когато и двата аргумента са равни на 0.
Означава се с v или с OR, например aORb или avb.
Таблица за истинност:

В) Инверсия (!, NOT, ¬ )
логическо отрицание – инверсия – има един аргумент и променя стойността му от 1 в 0 или обратно от 0 в 1. Срещат се различни варианти на означаване - !,NOT,¬ .
Таблица за истинност:

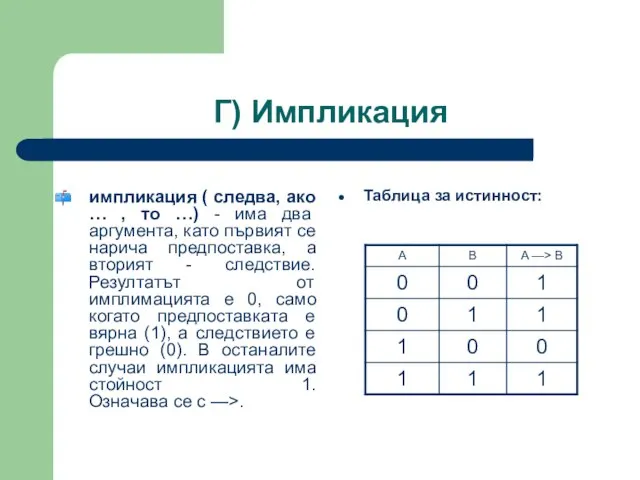
Г) Импликация
импликация ( следва, ако … , то …) - има два аргумента, като първият се нарича предпоставка, а вторият - следствие. Резултатът от имплимацията е 0, само когато предпоставката е вярна (1), а следствието е грешно (0). В останалите случаи импликацията има стойност 1.
Означава се с —>.
Таблица за истинност:

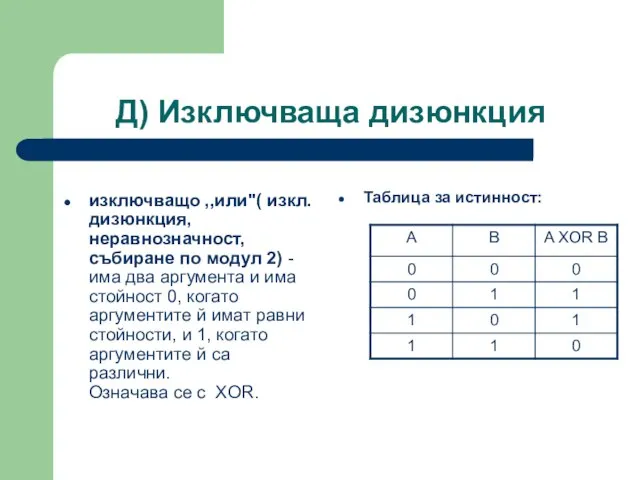
Д) Изключваща дизюнкция
изключващо ,,или"( изкл. дизюнкция, неравнозначност, събиране по модул 2) - има два аргумента и има стойност 0, когато аргументите й имат равни стойности, и 1, когато аргументите й са различни.
Означава се с XOR.
Таблица за истинност:

Е) Равнозначност
равнозначност - има два аргумента и има стойност 0, когато аргументите й имат различни стойности, и 1, когато аргументите й са равни.
Означава се с <—>.
Таблица за истинност:

4. Закони на Де Морган
А) ¬(X ^ Y) = ¬X v ¬Y
Б) ¬(X v Y) = ¬X ^ ¬ Y

А) ¬(X ^ Y) = ¬X v ¬Y
Отрицанието на конюнкцията е равно на дизюнкцията на отрицанията.

Б) ¬(X v Y) = ¬X ^ ¬ Y
Отрицанието на дизюнкцията е равно на конюнкцията на отрицанията.

5. Пресмятане на съждителни изрази

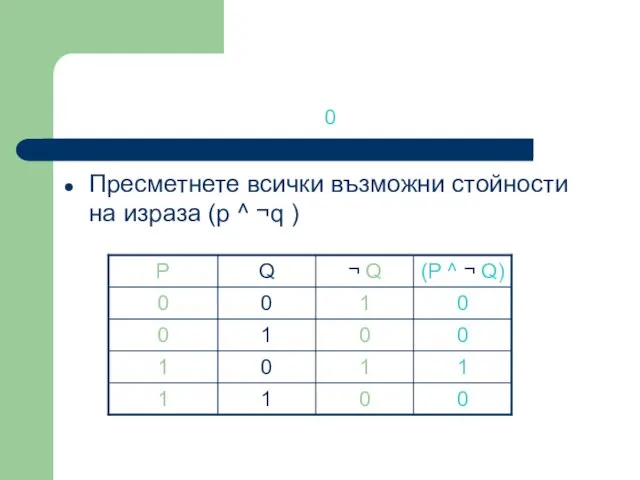
0
Пресметнете всички възможни стойности на израза (p ^ ¬q )

6. Логически елементи на компютъра
това са електронни логически схеми, които реализират елементарни логически функции.

Логическите елементи на компютъра се явяват електронните схеми И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и други.

Всеки логически елемент има свое условно обозначение, което изразява неговата логическа функция, но не указва с каква именно електронна схема в него е реализиран. Това опростява записа и разбирането на сложни логически схеми.

Това е таблично представяне на логическите схеми (операции), в които са изчислени всички възможни съчетания на значението на истинност на входните сигнали (операнди) заедно със значението на истинност на изходните сигнали (резултат от операцията) за всяко от тези съчетания.
Таблица на истинност

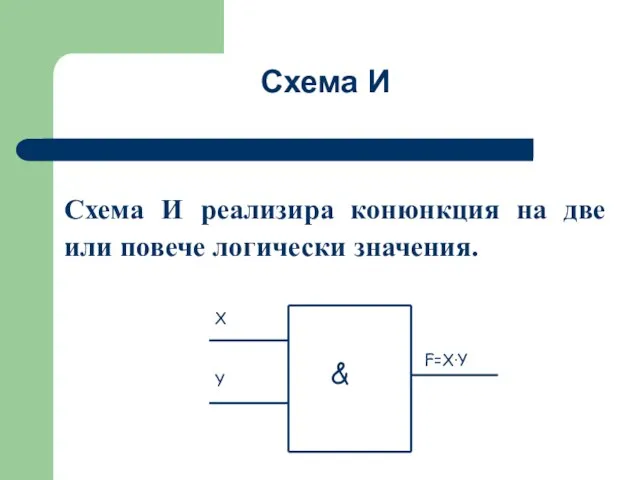
Схема И реализира конюнкция на две или повече логически значения.
Схема И

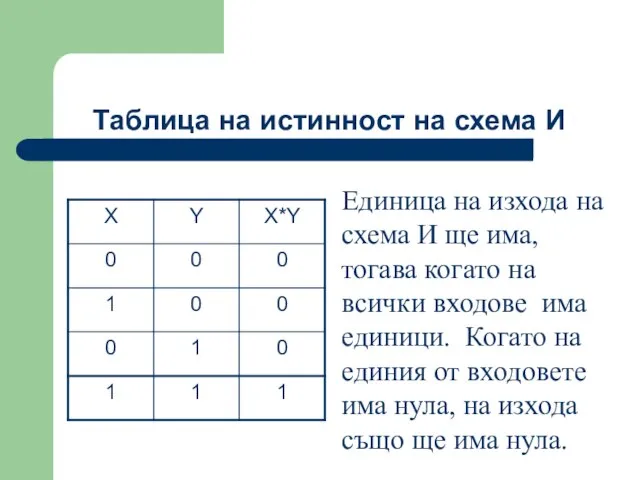
Единица на изхода на схема И ще има, тогава когато на всички входове има единици. Когато на единия от входовете има нула, на изхода също ще има нула.
Таблица на истинност на схема И

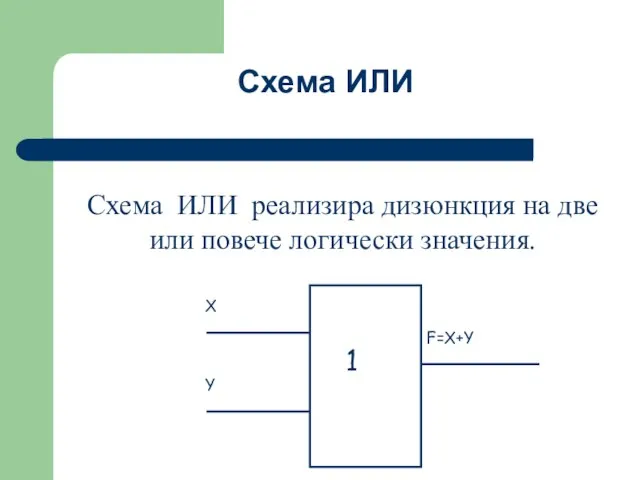
Схема ИЛИ реализира дизюнкция на две или повече логически значения.
Схема ИЛИ

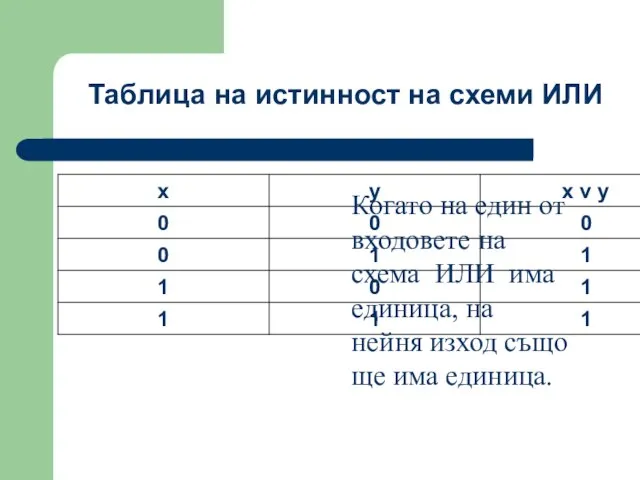
Таблица на истинност на схеми ИЛИ
Когато на един от входовете на схема ИЛИ има единица, на нейня изход също ще има единица.

Схема НЕ (инвертор) реализира операцията отрицание. Връзката между входа x на тези схеми и изхода F може да се запише със съотношението F = x където х се чете като "не x" или "инверсия х".
С х е м а НЕ

Таблица на истинност на схема НЕ
Ако на входа на схемата е 0, то на изхода е 1. Когато на входа е 1, на изхода е 0.

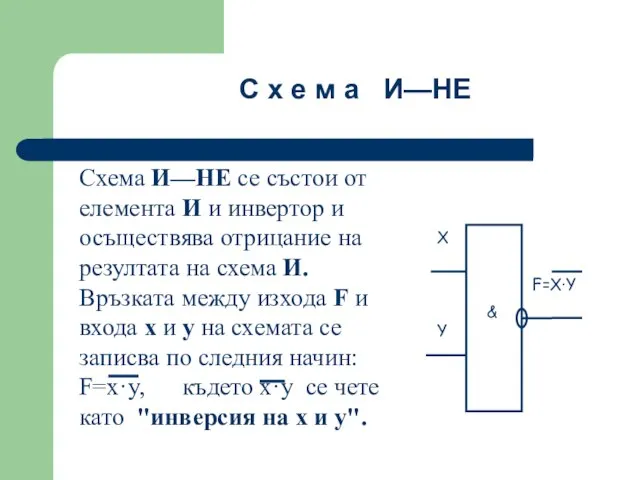
Схема И—НЕ се състои от елемента И и инвертор и осъществява отрицание на резултата на схема И. Връзката между изхода F и входа x и y на схемата се записва по следния начин: F=x·y, където x·y се чете като "инверсия на x и y".
С х е м а И—НЕ

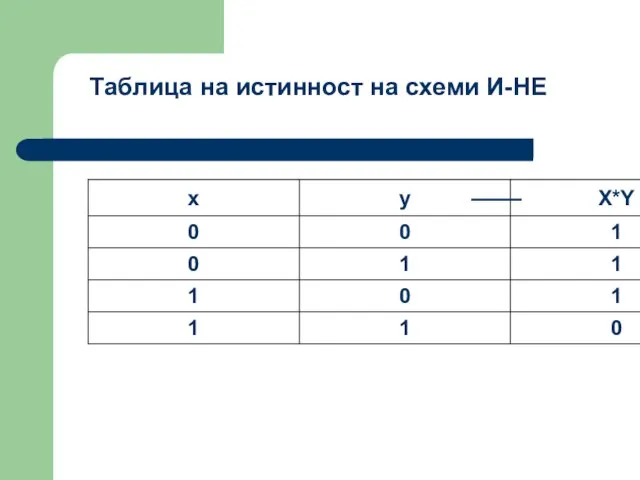
Таблица на истинност на схеми И-НЕ

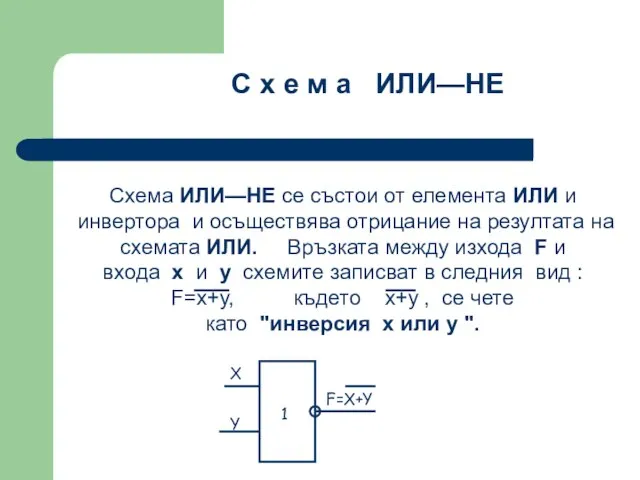
Схема ИЛИ—НЕ се състои от елемента ИЛИ и инвертора и осъществява отрицание на резултата на схемата ИЛИ. Връзката между изхода F и входа x и y схемите записват в следния вид : F=x+y, където x+y , се чете като "инверсия x или y ".
С х е м а ИЛИ—НЕ

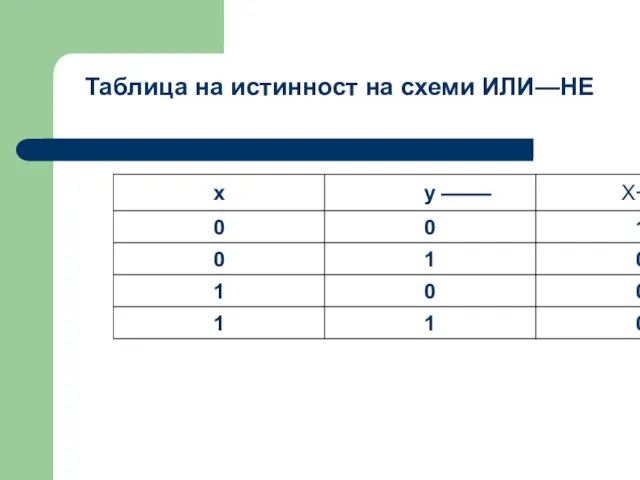
Таблица на истинност на схеми ИЛИ—НЕ

Това е електронна схема, широко използвана в регистрите на компютъра за надеждно запомняне на един разряд двоичен код. Тригера има две устойчиви състояния, едното от които съответствува на двоична единица, а другото на двоична нула.
Тригер

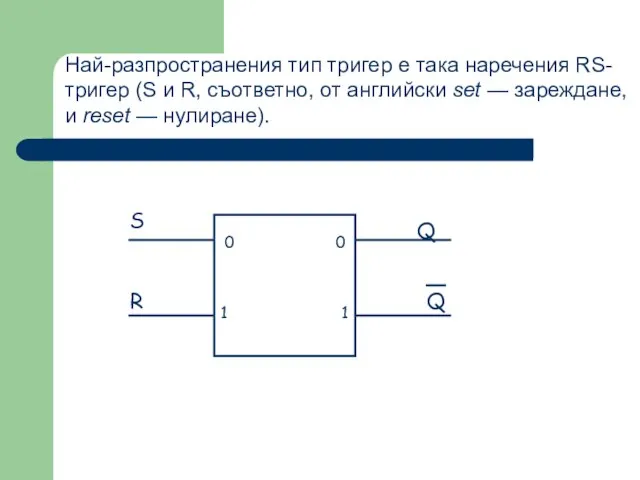
Най-разпространения тип тригер е така наречения RS-тригер (S и R, съответно, от английски set — зареждане, и reset — нулиране).
0
1
0
1
S
R
Q
Q

Това е електронна логическа схема, извършваща сумиране на двоични числа.
Суматора служи, преди всичко, като централен възел на аритметико-логическото устройство на компютъра, като намира приложение също и в други устройства и машини.
Суматор