Алгоритмы сортировки массивов.

Сортировка является одной из фундаментальных алгоритмических задач программирования. Решению проблем, связанных с сортировкой, посвящено множество научных исследований, разработано множество алгоритмов.
В общем случае сортировку следует понимать как процесс перегруппировки, заданного множества объектов в определенном порядке. Сортировка применяется во всех без исключения областях программирования, будь то базы данных или математические программы.
Алгоритмом сортировки называется алгоритм для упорядочения некоторого множества элементов. Обычно под алгоритмом сортировки подразумевают алгоритм упорядочивания множества элементов по возрастанию или убыванию.
В случае наличия элементов с одинаковыми значениями, в упорядоченной последовательности они располагаются рядом друг за другом в любом порядке. Однако иногда бывает полезно сохранять первоначальный порядок элементов с одинаковыми значениями.
В алгоритмах сортировки лишь часть данных используется в качестве ключа сортировки. Ключом сортировки называется атрибут (или несколько атрибутов), по значению которого определяется порядок элементов. Таким образом, при написании алгоритмов сортировок массивов следует учесть, что ключ полностью или частично совпадает с данными.

Практически каждый алгоритм сортировки можно разбить на 3 части:
сравнение, определяющее упорядоченность пары элементов;
перестановку, меняющую местами пару элементов;
собственно сортирующий алгоритм, который осуществляет сравнение и перестановку элементов до тех пор, пока все элементы множества не будут упорядочены.
Алгоритмы сортировки имеют большое практическое применение. Их можно встретить там, где речь идет об обработке и хранении больших объемов информации. Некоторые задачи обработки данных решаются проще, если данные заранее упорядочить.

Оценка алгоритмов сортировки
Ни одна другая проблема не породила такого количества разнообразнейших решений, как задача сортировки. Универсального, наилучшего алгоритма сортировки на данный момент не существует. Однако, имея приблизительные характеристики входных данных, можно подобрать метод, работающий оптимальным образом. Для этого необходимо знать параметры, по которым будет производиться оценка алгоритмов.
Время сортировки – основной параметр, характеризующий быстродействие алгоритма.
Память – один из параметров, который характеризуется тем, что ряд алгоритмов сортировки требуют выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив данных и независящие от входной последовательности затраты, например, на хранение кода программы.
Устойчивость – это параметр, который отвечает за то, что сортировка не меняет взаимного расположения равных элементов.
Естественность поведения – параметр, который указывает на эффективность метода при обработке уже отсортированных, или частично отсортированных данных. Алгоритм ведет себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.

Классификация алгоритмов сортировок
Все разнообразие и многообразие алгоритмов сортировок можно классифицировать по различным признакам, например,
по устойчивости,
по поведению,
по использованию операций сравнения,
по потребности в дополнительной памяти,
по потребности в знаниях о структуре данных, выходящих за рамки операции сравнения, и другие.
Рассмотрим классификацию алгоритмов сортировки по сфере применения. В данном случае основные типы упорядочивания делятся следующим образом:
Внутренняя сортировка
Внешняя сортировка

Внутренняя сортировка – это алгоритм сортировки, который в процессе упорядочивания данных использует только оперативную память (ОЗУ) компьютера.
Т.е. оперативной памяти достаточно для помещения в нее сортируемого массива данных с произвольным доступом к любой ячейке и собственно для выполнения алгоритма.
Внутренняя сортировка применяется во всех случаях, за исключением однопроходного считывания данных и однопроходной записи отсортированных данных. В зависимости от конкретного алгоритма и его реализации данные могут сортироваться в той же области памяти, либо использовать дополнительную оперативную память.

Внешняя сортировка – это алгоритм сортировки, который при проведении упорядочивания данных использует внешнюю память, например, жесткие диски.
Внешняя сортировка разработана для обработки больших списков данных, которые не помещаются в оперативную память. Обращение к различным носителям накладывает некоторые дополнительные ограничения на данный алгоритм: доступ к носителю осуществляется последовательным образом, то есть в каждый момент времени можно считать или записать только элемент, следующий за текущим; объем данных не позволяет им разместиться в ОЗУ.

Внутренняя сортировка является базовой для любого алгоритма внешней сортировки – отдельные части массива данных сортируются в оперативной памяти и с помощью специального алгоритма сцепляются в один массив, упорядоченный по ключу.
Следует отметить, что внутренняя сортировка значительно эффективней внешней, так как на обращение к оперативной памяти затрачивается намного меньше времени, чем к носителям.

Основные алгоритмы внутренних сортировок

Сортировка выбором.
Sortimine valiku abil.
Tom
Debby
Mike
Ron
Ron
Tom
Debby
Mike
Ron
Ron
Tom
Tom
Debby
Mike
Ron
Ron
Tom
Mike

50
20
40
75
35
A[0] A[1] A[2] A[3] A[4]
Valime 20 ja vahetame A[0]-ga
20
50
40
75
35
Valime 35 ja vahetame A[1]-ga
20
35
40
75
50
Valime 40 ja vahetame A[2]-ga
20
35
40
75
50
Valime 50 ja vahetame A[3]-ga
20
35
40
50
75
Valmis
Kokku n elementi. Teeme vahetamisest n-1 korda

void SelectionSort (
A[ ], int n)
{ int v_Index; //kõige väiksema elemendi index int i, j; //tsykli loendurid
for (i=0; i
{ v_Index=i;
for (j=i+1; j
{
//kui paremal element on suurem, vahetame
//neid kohtadega
if (A[j] < A[v_Index]) v_Index=j;
vaheta(A[i], A[v_Index]);
}
}

Сортировка методом пузырька.
Mulli meetodi sortimine.
50
20
40
75
35
A[0] A[1] A[2] A[3] A[4]
Vahetame 20 ja 50
20
50
40
75
35
Vahetame 50 ja 40
20
40
50
75
35
50 ja 75 oma kohtadel
20
40
50
75
35
Vahetame 35 ja 75
20
40
50
35
75
75 kõige suurem element.
LastExchangeIndex = 3
Läbimine 0
Проход 0

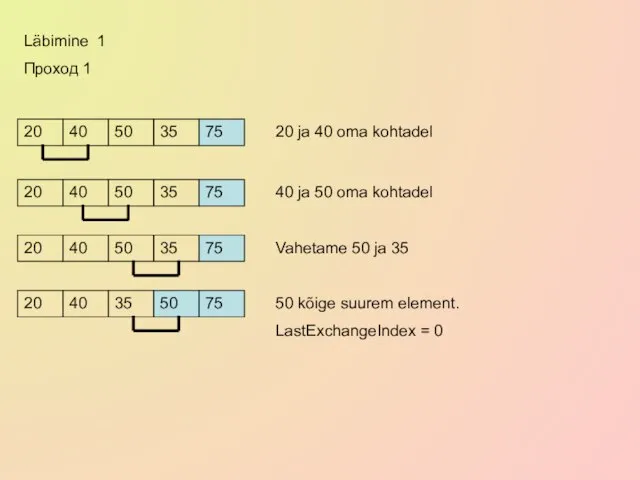
20
40
50
35
75
20 ja 40 oma kohtadel
20
40
50
35
75
40 ja 50 oma kohtadel
20
40
50
35
75
Vahetame 50 ja 35
20
40
35
50
75
50 kõige suurem element.
LastExchangeIndex = 0
Läbimine 1
Проход 1

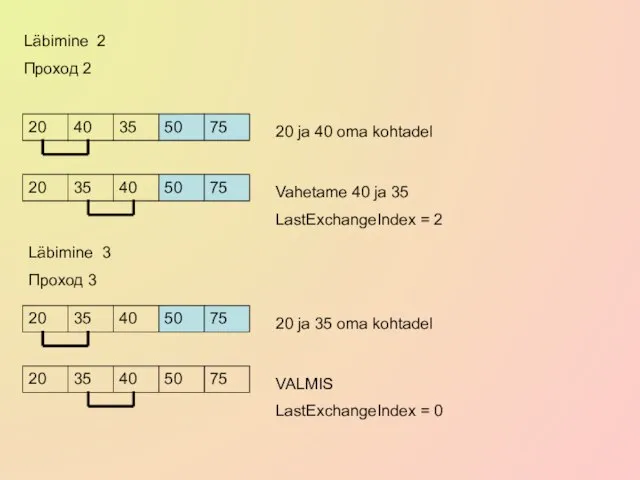
Läbimine 2
Проход 2
20
40
35
50
75
20 ja 40 oma kohtadel
20
35
40
50
75
Vahetame 40 ja 35
LastExchangeIndex = 2
Läbimine 3
Проход 3
20
35
40
50
75
20 ja 35 oma kohtadel
20
35
40
50
75
VALMIS
LastExchangeIndex = 0

void BubbleSort (
A[ ], int n)
{
int i, j;
//viimase vahetamise elemendi index int ViimaneIndex;
i=n-1;
while (i>0)
{
for (j=0; j
if (A[ j+1 ] < A [ j ])
{
Vaheta(A[j], A[j+1]);
ViimaneIndex =j;
}
i= ViimaneIndex;
}
}

50
20
40
75
35
A[0] A[1] A[2] A[3] A[4]
Сортировка вставкой.
50
Alustame 50-st
Andmetöötlus: 20
50
A[0]=20 ja A[1]=50
20
Andmetöötlus: 40
40
A[1]=40 ja A[2]=50
20
50
Andmetöötlus: 75
40
75 on oma kohal
20
50
75
Andmetöötlus: 35
40
A[1]=35
Nihutamine paremale
20
50
75
35

void InsertionSort (
A[ ], int n)
{
int i, j;
T temp;
for (i=1; i
{
j=i;
temp=A[i];
while (j>0 && temp
{
A[j]=A[j-1];
j--;
}
A[j]=temp;
}
}

"Поразрядная сортировка"
Поразрядная сортировка была изобретена в 1920-х годах как побочный результат использования сортирующих машин. Такая машина обрабатывала перфокарты, имевшие по 80 колонок. Каждая колонка представляла отдельный символ. В колонке было 12 позиций, и в них для представления того или иного символа пробивались отверстия. Цифру от 0 до 9 кодировали одним отверстием в соответствующей позиции (еще две позиции в колонке использовали для кодировки букв).
Запуская машину, оператор закладывал в ее приемное устройство стопку перфокарт и задавал номер колонки на перфокартах. Машина "просматривала" эту колонку на картах и по цифровому значению 0, 1, ..., 9 в ней распределяла ("сортировала") карты на 10 стопок.
Несколько колонок (разрядов) с закодированными цифрами представляли натуральное число, т.е. номер. Чтобы получить стопку карт, упорядоченных по номерам, оператор действовал так. Вначале он распределял карты на 10 стопок по значению младшем разряде. Эти стопки в порядке возрастания значений в младшем разряде он складывал в одну и повторял процесс, но со следующим разрядом, и т.д. Получив стопки карт, распределенных по значениям в старшем разряде, оператор складывал их по возрастанию этих значений и получал то, что нужно.

Значения в разрядах номеров заданы цифрами, поэтому поразрядную сортировку еще называют цифровой. Заметим, что цифры от 0 до 9 упорядочены по возрастанию, поэтому цифровая сортировка располагает числа в лексикографическом порядке.
Пример.
Входные данные
Выходные данные
733 877 323 231 777 721 123
123 231 323 721 733 777 877
Описание решения.
Принцип решения разберем на конкретном примере. Пусть задана последовательность трехзначных номеров:
733 877 323 231 777 721 123
Распределим данную последовательность по младшей цифре на стопки:
231 721
733 323 123
877 777

Далее сложим получившиеся стопки в одну в порядке возрастания последней цифры.
231 721 733 323 123 877 777
На следующем шаге номера, которые обрабатываются именно в этой последовательности, распределяются по второй цифре на следующие стопки.
721 323 123
231 733
877 777
Затем из них также образуется одна последовательность.
721 323 123 231 733 877 777
Обратим внимание, что перед последним шагом все номера с числом сотен 7, благодаря предыдущим шагам, расположены один относительно другого по возрастанию.
На последнем шаге номера распределяются по старшей цифре на стопки:
123
231
323
721 733 777
877
и образуется окончательная последовательность:
123 231 323 721 733 777 877.

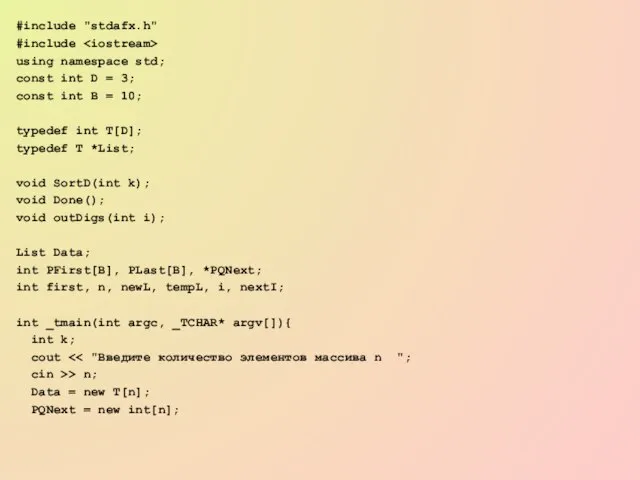
#include "stdafx.h"
#include
using namespace std;
const int D = 3;
const int B = 10;
typedef int T[D];
typedef T *List;
void SortD(int k);
void Done();
void outDigs(int i);
List Data;
int PFirst[B], PLast[B], *PQNext;
int first, n, newL, tempL, i, nextI;
int _tmain(int argc, _TCHAR* argv[]){
int k;
cout << "Введите количество элементов массива n ";
cin >> n;
Data = new T[n];
PQNext = new int[n];

for ( k = 0 ; k < n ; k++ ){ PQNext[k] = k + 1;
for ( int r = 0 ; r < D ; r++ )
Data[k][r] = 0;
}
for ( k = 0 ; k < n ; k++ )
for ( int r = 0 ; r < D ; r++ )
Data[k][r] = rand()%B;
first = 0;
Done();
cout << endl;
for ( k = D - 1 ; k >= 0 ; k-- )
SortD(k);
Done();
cout << endl;
delete [] PQNext;
delete [] Data;
system("pause");
return 0;
}

// описание функции поразрядной сортировки
void SortD(int k){
for ( tempL = 0 ; tempL < B ; tempL++ ){
PFirst[tempL] = n;
PLast[tempL] = n;
}
i = first;
while (i != n){
tempL = Data[i][k];
nextI = PQNext[i];
PQNext[i] = n;
if ( PFirst[tempL] == n )
PFirst[tempL] = i;
else PQNext[PLast[tempL]] = i;
PLast[tempL] = i;
i = nextI;
}
tempL = 0;
while ( tempL < B && PFirst[tempL] == n )
tempL++;
first = PFirst[tempL];

while ( tempL < B - 1 ){
newL = tempL + 1;
while ( newL < B && PFirst[newL] == n )
newL++;
if ( newL < B )
PQNext[PLast[tempL]] = PFirst[newL];
tempL = newL;
}
}
/*описание функции вывода элементов в соответсвии со списком индесов в массиве PQNext*/
void Done(){
int i = first;
while ( i != n ){
outDigs(i);
i = PQNext[i];
}
}

/*описание функции вывода элементов из массива Data, индекс которого задан ее аргументом*/
void outDigs(int i){
int j = 0;
while ( Data[i][j] == 0 && j < D )
j++;
if ( j == D )
cout << 0;
else
while ( j < D )
cout << Data[i][j++];
cout << " ";
}

Данный метод сортировки был предложен Дж.Уильямсом и Р.У. Флойдом в 1964 году. Пирамидальная сортировка в некотором роде является модификацией такого подхода, как сортировка выбором, с тем лишь отличием, что минимальный (или максимальный) элемент из неотсортированной последовательности выбирается за меньшее количество операций. Для такого быстрого выбора из этой неотсортированной последовательности строится некоторая структура. Именно суть данного метода и состоит в построении такой структуры, которая называется пирамидой.
Пирамида (сортирующее дерево, двоичная куча) – двоичное дерево с упорядоченными листьями (корень дерева – наименьший или наибольший элемент). Пирамиду можно представить в виде массива. Первый элемент пирамиды является наименьшим или наибольшим, что зависит от ключа сортировки.
Бинарная пирамидальная сортировка

Просеивание – это построение новой пирамиды по следующему алгоритму:
новый элемент помещается в вершину дерева, далее он перемещается ("просеивается") по пути вниз на основе сравнения с дочерними элементами. Спуск завершается, если результат сравнения с дочерними элементами соответствует ключу сортировки.
Последовательность чисел xi,xi+1,...,xi формирует пирамиду, если для всех k=i, i+1,...,n/2 выполняются неравенства xk > x2k, xk > xi (или xk < x2k, xk < x2k+1). Элементы x2i и x2i+1 называются потомками элемента xi.
Массив чисел 12 10 7 5 8 7 3 является пирамидой. Такой массив удобно изображать в виде дерева. Первый элемент массива, элементы которого образуют собой пирамиду, является наибольшим (или наименьшим). Если массив представлен в виде пирамиды, то массив легко отсортировать.

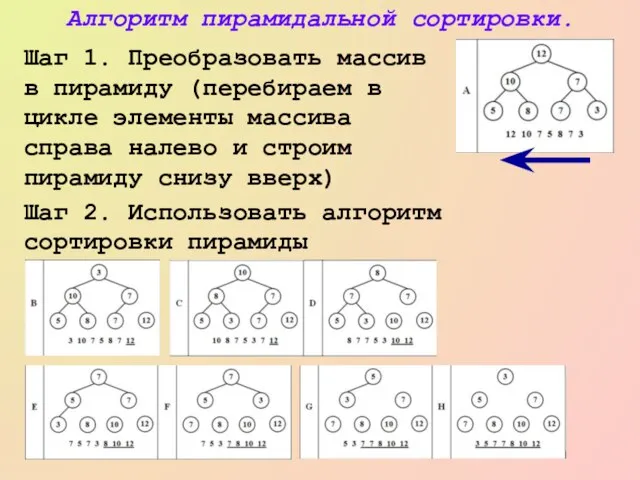
Алгоритм пирамидальной сортировки.
Шаг 1. Преобразовать массив в пирамиду (перебираем в цикле элементы массива справа налево и строим пирамиду снизу вверх)
Шаг 2. Использовать алгоритм сортировки пирамиды

Алгоритм преобразования массива в пирамиду (построение пирамиды).
Пусть дан массив x[1],x[2],...,x[n].
Шаг 1. Устанавливаем k=n/2.
Шаг 2. Перебираем элементы массива в цикле справа налево для i=k,k-1,...,1. Если неравенства xi > x2i, xi > x2i+1 не выполняются, то повторяем перестановки xi с наибольшим из потомков. Перестановки завершаются при выполнении неравенств xi > x2i, xi > x2i+1.

Алгоритм сортировки пирамиды.
Рассмотрим массив размерности n, который представляет пирамиду x[1],x[2],...,x[n](см.рис.А).
Шаг 1. Переставляем элементы x[1] и x[n] (см.рис.В).
Шаг 2. Определяем n=n-1. Это эквивалентно тому, что в массиве из дальнейшего рассмотрения исключается элемент x[n].

Шаг 3. Рассматриваем массив x[1],x[2],...,x[n-1], который получается из исходного за счет исключения последнего элемента. Данный массив из-за перестановки элементов уже не является пирамидой. Но такой массив легко преобразовать в пирамиду. Это достигается повторением перестановки значения элемента из x[1] с наибольшим из потомков. Такая перестановка продолжается до тех пор, пока элемент из x[1] не окажется на месте элемента x[i] и при этом будут выполняться неравенства x[i] > x[2i], x[i] > x[2i+1]. Тем самым определяется новое место для значения первого элемента из x[1](см.рис.С).
Шаг 4. Повторяем шаги 2, 3, 4 до тех пор, пока не получим n=1. Произвольный массив можно преобразовать в пирамиду (см.рис. D, E, F, G, H).

Построение пирамиды, ее сортировка и "просеивание" элементов реализуются с помощью рекурсии. Базой рекурсии при этом выступает пирамида из одного элемента, а сортировка и просеивание элементов сводятся посредством декомпозиции к аналогичным действиям с пирамидой из n-1 элемента.
#include
#include
#include
#include
#define n 100
using namespace std;
//процедура обмена двух элементов
void Exchange (int i, int j, int *x)
{
int tmp;
tmp = x[i];
x[i] = x[j];
x[j] = tmp;
}
//"Просеивание" элементов
void Sifting (int left, int right, int *x){
int q, p, h;
q=2*left+1;
p=q+1;
if (q <= right){
if (p <= right && x[p] > x[q])
q = p;
if (x[left] < x[q]){
Exchange (left, q, x);
Sifting(q, right, x);
}
}
}

//Построение пирамиды
void Build_Pyramid (int k, int r, int *x){
Sifting(k,r,x);
if (k > 0)
Build_Pyramid(k-1,r,x);
}
//Сортировка пирамиды
void Sort_Piramid (int k, int *x){
Exchange (0,k,x);
Sifting(0,k-1,x);
if (k > 1)
Sort_Piramid(k-1,x);
}
//Описание функции бинарной пирамидальной сортировки
void Binary_Pyramidal_Sort (int k,int *x){
Build_Pyramid(k/2+1,k-1,x);
Sort_Piramid(k-1,x);
}
void main()
{
int x[n], j;
srand( (unsigned)time( NULL ) );
for(j=0;j
cout<<"Sozdan massiiv \n“;

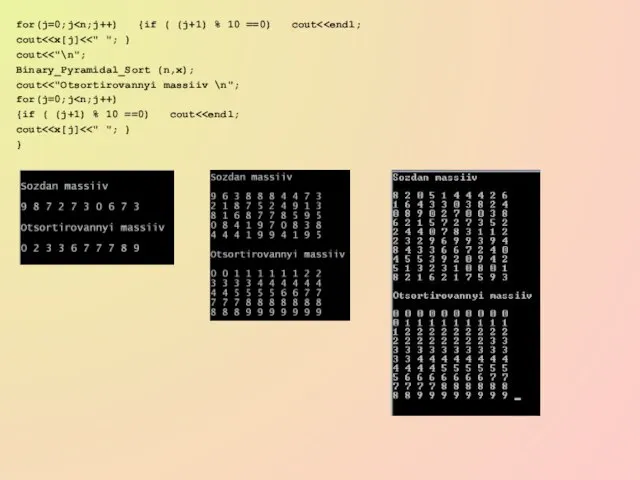
for(j=0;j
cout<
cout<<"\n";
Binary_Pyramidal_Sort (n,x);
cout<<"Otsortirovannyi massiiv \n";
for(j=0;j
{if ( (j+1) % 10 ==0) cout<
cout<
}

Теоретическое время работы этого алгоритма можно оценить, учитывая, что пирамидальная сортировка аналогична построению пирамиды методом просеивания (при этом не учитывается начальное построение пирамиды). Поэтому время работы алгоритма пирамидальной сортировки без учета времени построения пирамиды будет определяться по формуле T1(n)=O(n·log n).
Построение пирамиды занимает T2(n)=O(n) операций за счет того, что реальное время выполнения функции построения зависит от высоты уже созданной части пирамиды.
Тогда общее время сортировки (с учетом построения пирамиды) будет равно: T(n)=T1(n)+T2(n)=O(n)+O(n·log n)=O(n·log n).
Пирамидальная сортировка не использует дополнительной памяти.
Метод не является устойчивым: по ходу работы массив так "перетряхивается", что исходный порядок элементов может измениться случайным образом. Поведение неестественно: частичная упорядоченность массива никак не учитывается. Данная сортировка на почти отсортированных массивах работает также долго, выигрыш ее получается только на больших n.

Сортировка методом Шелла
Сортировка Шелла была названа в честь ее изобретателя – Дональда Шелла, который опубликовал этот алгоритм в 1959 году. Общая идея сортировки Шелла состоит в сравнении на начальных стадиях сортировки пар значений, расположенных достаточно далеко друг от друга в упорядочиваемом наборе данных. Такая модификация метода сортировки позволяет быстро переставлять далекие неупорядоченные пары значений (сортировка таких пар обычно требует большого количества перестановок, если используется сравнение только соседних элементов).
Метод, предложенный Дональдом Л. Шеллом, является неустойчивой сортировкой по месту. Эффективность метода Шелла объясняется тем, что сдвигаемые элементы быстро попадают на нужные места.

Общая схема метода:
Шаг 1. Происходит упорядочивание элементов n/2 пар (xi,xn/2+i) для 1
Шаг 2. Упорядочиваются элементы в n/4 группах из четырех элементов (xi,xn/4+i,xn/2+i,x3n/4+i) для 1
Шаг 3. Упорядочиваются элементы уже в n/4 группах из восьми элементов и т.д. На последнем шаге упорядочиваются элементы сразу во всем массиве x1,x2,...,xn. На каждом шаге для упорядочивания элементов в группах используется метод сортировки вставками.

#include
#include
#include
#define k 10
using namespace std;
//процедура обмена двух элементов
void Exchange (int i, int j, int *x)
{
int tmp;
tmp = x[i];
x[i] = x[j];
x[j] = tmp;
}
//Описание функции сортировки Шелла
void Shell_Sort (int n, int *x)
{
int h, i, j;
for (h = n/2 ; h > 0 ; h = h/2)
for (i = 0 ; i < n-h ; i++)
for (j = i ; j >= 0 ; j = j - h)
if (x[j] > x[j+h])
Exchange (j, j+h, x);
else j = 0;
}
void main()
{
int x[k], j;
srand( (unsigned)time( NULL ) );
for(j=0;j
cout<<"\nSozdan massiiv \n";
for(j=0;j
cout<
cout<<"\n";
Shell_Sort (k, x);
cout<<"\nOtsortirovannyi massiiv \n";
for(j=0;j
{if ( (j) % 10 ==0) cout<
cout<
getch();
}

Быстрая сортировка Хоара
Метод быстрой сортировки был впервые описан Ч.А.Р. Хоаром в 1962 году. Быстрая сортировка – это общее название ряда алгоритмов, которые отражают различные подходы к получению критичного параметра, влияющего на производительность метода.
При общем рассмотрении алгоритма быстрой сортировки, отметим, что этот метод основывается на последовательном разделении сортируемого набора данных на блоки меньшего размера таким образом, что между значениями разных блоков обеспечивается отношение упорядоченности (для любой пары блоков все значения одного из этих блоков не превышают значений другого блока).
Опорным (ведущим) элементом называется некоторый элемент массива, который выбирается определенный образом. С точки зрения корректности алгоритма выбор опорного элемента безразличен. С точки зрения повышения эффективности алгоритма выбираться должна медиана, но без дополнительных сведений о сортируемых данных ее обычно невозможно получить. Необходимо выбирать постоянно один и тот же элемент (например, средний или последний по положению) или выбирать элемент со случайно выбранным индексом.

Алгоритм быстрой сортировки Хоара
Пусть дан массив x[n] размерности n.
Шаг 1. Выбирается опорный элемент массива.
Шаг 2. Массив разбивается на два – левый и правый – относительно опорного элемента. Реорганизуем массив таким образом, чтобы все элементы, меньшие опорного элемента, оказались слева от него, а все элементы, большие опорного – справа от него.
Шаг 3. Далее повторяется шаг 2 для каждого из двух вновь образованных массивов. Каждый раз при повторении преобразования очередная часть массива разбивается на два меньших и т. д., пока не получится массив из двух элементов (см. рис. На следующем слайде)
Быстрая сортировка стала популярной прежде всего потому, что ее нетрудно реализовать, она хорошо работает на различных видах входных данных и во многих случаях требует меньше затрат ресурсов по сравнению с другими методами сортировки.
Выберем в качестве опорного элемент, расположенный на средней позиции.

//Описание функции сортировки Хоара
void Hoar_Sort (int k, int *x){
Quick_Sort (0, k-1, x);
}
void Quick_Sort(int left, int right, int *x){
int i, j, m, h;
i = left;
j = right;
m = x[(i+j+1)/2];
do {
while (x[i] < m) i++;
while (x[j] > m) j--;
if (i <= j) {
Exchange(i,j,x);
i++;
j--;
}
} while(i <= j);
if (left < j)
Quick_Sort (left, j, x);
if (i < right)
Quick_Sort (i, right, x);
}
//процедура обмена двух элементов
void Exchange (int i, int j, int *x){
int tmp;
tmp = x[i];
x[i] = x[j];
x[j] = tmp;
}

Эффективность быстрой сортировки в значительной степени определяется правильностью выбора опорных (ведущих) элементов при формировании блоков. В худшем случае трудоемкость метода имеет ту же сложность, что и пузырьковая сортировка, то есть порядка O(n2). При оптимальном выборе ведущих элементов, когда разделение каждого блока происходит на равные по размеру части, трудоемкость алгоритма совпадает с быстродействием наиболее эффективных способов сортировки, то есть порядка O(n log n). В среднем случае количество операций, выполняемых алгоритмом быстрой сортировки, определяется выражением T(n) = O(1.4n log n)
Быстрая сортировка является наиболее эффективным алгоритмом из всех известных методов сортировки, но все усовершенствованные методы имеют один общий недостаток – невысокую скорость работы при малых значениях n.
Рекурсивная реализация быстрой сортировки позволяет устранить этот недостаток путем включения прямого метода сортировки для частей массива с небольшим количеством элементов. Анализ вычислительной сложности таких алгоритмов показывает, что если подмассив имеет девять или менее элементов, то целесообразно использовать прямой метод (сортировку простыми вставками).

Сортировка слиянием
Алгоритм сортировки слиянием был изобретен Джоном фон Нейманом в 1945 году. Он является одним из самых быстрых способов сортировки.
Слияние – это объединение двух или более упорядоченных массивов в один упорядоченный.
Сортировка слиянием является одним из самых простых алгоритмов сортировки (среди быстрых алгоритмов).
Особенностью этого алгоритма является то, что он работает с элементами массива преимущественно последовательно, благодаря чему именно этот алгоритм используется при сортировке в системах с различными аппаратными ограничениями (например, при сортировке данных на жестком диске).
Кроме того, сортировка слиянием является алгоритмом, который может быть эффективно использован для сортировки таких структур данных, как связанные списки.

Данный алгоритм применяется тогда, когда есть возможность использовать для хранения промежуточных результатов память, сравнимую с размером исходного массива. Он построен на принципе "разделяй и властвуй". Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Далее их решения комбинируются, и получается решение исходной задачи.
Процедура слияния требует два отсортированных массива. Заметим, что массив из одного элемента по определению является отсортированным.

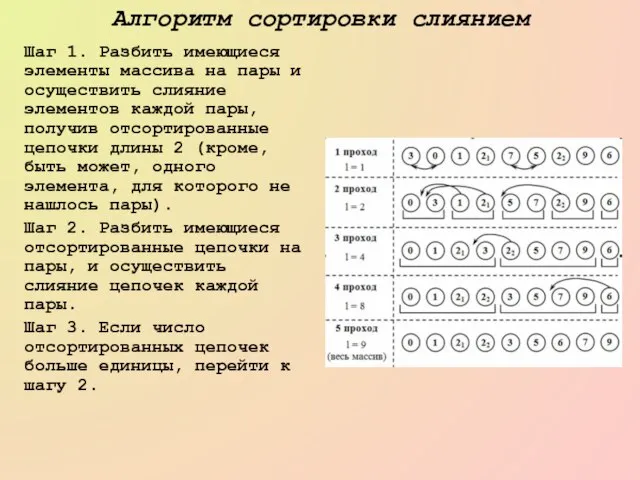
Алгоритм сортировки слиянием
Шаг 1. Разбить имеющиеся элементы массива на пары и осуществить слияние элементов каждой пары, получив отсортированные цепочки длины 2 (кроме, быть может, одного элемента, для которого не нашлось пары).
Шаг 2. Разбить имеющиеся отсортированные цепочки на пары, и осуществить слияние цепочек каждой пары.
Шаг 3. Если число отсортированных цепочек больше единицы, перейти к шагу 2.

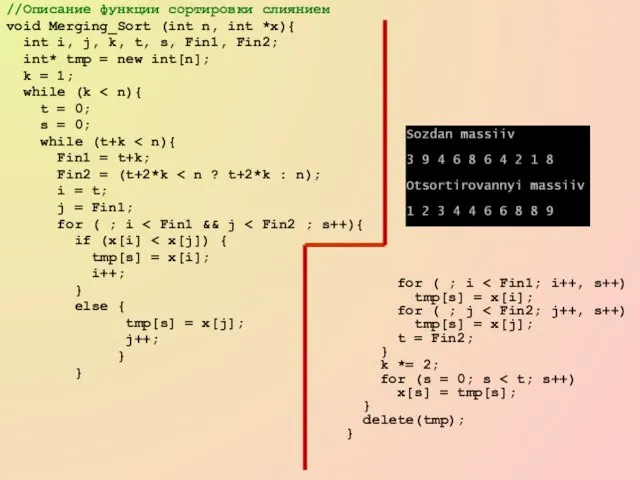
//Описание функции сортировки слиянием
void Merging_Sort (int n, int *x){
int i, j, k, t, s, Fin1, Fin2;
int* tmp = new int[n];
k = 1;
while (k < n){
t = 0;
s = 0;
while (t+k < n){
Fin1 = t+k;
Fin2 = (t+2*k < n ? t+2*k : n);
i = t;
j = Fin1;
for ( ; i < Fin1 && j < Fin2 ; s++){
if (x[i] < x[j]) {
tmp[s] = x[i];
i++;
}
else {
tmp[s] = x[j];
j++;
}
}
for ( ; i < Fin1; i++, s++)
tmp[s] = x[i];
for ( ; j < Fin2; j++, s++)
tmp[s] = x[j];
t = Fin2;
}
k *= 2;
for (s = 0; s < t; s++)
x[s] = tmp[s];
}
delete(tmp);
}

Недостаток алгоритма заключается в том, что он требует дополнительную память размером порядка n (для хранения вспомогательного массива). Кроме того, он не гарантирует сохранение порядка элементов с одинаковыми значениями. Но его временная сложность всегда пропорциональна O(n log n).
Сравнение алгоритмов внутренней сортировки
Выше было рассмотрено достаточно большое количество алгоритмов внутренней сортировки. Возникает вопрос: зачем тогда нужно такое разнообразие алгоритмов сортировок, если есть возможность раз и навсегда определить алгоритм с наилучшим показателем эффективности и оставить «право на жизнь» исключительно за ним? Ответ прост: в реальных задачах имеются ограничения, определяемые как логикой задачи, так и свойствами конкретной вычислительной среды, которые могут существенно влиять на эффективность данной конкретной реализации алгоритма. Поэтому выбор того или иного алгоритма всегда остается за разработчиком программного обеспечения.

Теоретические временные и пространственные сложности рассмотренных методов сортировки

Таблица позволяет сделать ряд выводов.
1. На небольших наборах данных целесообразнее использовать сортировку включением, т.к. из всех методов, имеющих очень простую программную реализацию, этот на практике оказывается самым быстрым и при размерностях меньше ~3000 даёт вполне приемлемую для большинства случаев скорость работы. Еще одно преимущество этого метода заключается в том, что он использует полную или частичную упорядоченность входных данных и на упорядоченных данных работает быстрее, а на практике данные, как правило, уже имеют хотя бы частичный порядок.
2. Алгоритм пузырьковой сортировки, причем в той его модификации, которая не использует частичный порядок данных исходного массива, хотя и часто используется, но имеет плохие показатели даже среди простых методов с квадратичной сложностью.
3. Сортировка Шелла оказывается лишь красивым теоретическим методом, потому что на практике использовать его нецелесообразно: он сложен в реализации, но не дает такой скорости, какую дают сравнимые с ним по сложности программной реализации методы.
4. При сортировке больших массивов исходных данных лучше использовать быструю сортировку.

5. Если же добавляется требование гарантировать приемлемое время работы метода (быстрая сортировка в худшем случае имеет сложность, пропорциональную O(n2), хотя вероятность такого случая очень мала), то надо применять либо древесную сортировку, либо сортировку слиянием. Как видно из таблиц, сортировка слиянием работает быстрее, но следует помнить, что она требует дополнительную память размером порядка n.
6. В тех же случаях, когда есть возможность использовать дополнительную память размером порядка n, имеет смысл воспользоваться сортировкой распределением.

Задание
Дан целочисленный массив. Выполнить проверку уникальности элементов. Удалить из массива повторные вхождения чисел, предварительно отсортировав данные.

Внешняя сортировка – это сортировка данных, которые расположены на внешних устройствах и не вмещаются в оперативную память.
Внешние сортировки.

Внешние сортировки применяются к данным, которые хранятся во внешней памяти.
При выполнении таких сортировок требуется работать с данными, расположенными на внешних устройствах последовательного доступа.
Для файлов, расположенных на таких устройствах в каждый момент времени доступен только один компонент последовательности данных, что является существенным ограничением по сравнению с сортировкой массивов, где всегда доступен каждый элемент.

Данные, хранящиеся на внешних устройствах, имеют большой объем, что не позволяет их целиком переместить в оперативную память, отсортировать с использованием одного из алгоритмов внутренней сортировки, а затем вернуть их на внешнее устройство.
В этом случае осуществлялось бы минимальное количество проходов через файл, то есть было бы однократное чтение и однократная запись данных.
Однако на практике приходится осуществлять чтение, обработку и запись данных в файл по блокам, размер которых зависит от операционной системы и имеющегося объема оперативной памяти, что приводит к увеличению числа проходов через файл и заметному снижению скорости сортировки.
К наиболее известным алгоритмам внешних сортировок относятся:
сортировки слиянием:
простое слияние
естественное слияние
улучшенные сортировки:
многофазная сортировка
каскадная сортировка

Серия (упорядоченный отрезок) – это последовательность элементов, которая упорядочена (отсортирована) по ключу.
Длина серии - количество элементов в серии называется. Серия, состоящая из одного элемента, упорядочена всегда. Последняя серия может иметь длину меньшую, чем остальные серии файлов. Максимальное количество серий в файле N (все элементы не упорядочены). Минимальное количество серий одна (все элементы упорядочены).
Слияние – это процесс объединения двух (или более) упорядоченных серий в одну упорядоченную последовательность при помощи циклического выбора элементов доступных в данный момент.
Распределение – это процесс разделения упорядоченных серий на два и несколько вспомогательных файла.
Основные определения

Фаза – это действия по однократной обработке всей последовательности элементов.
Двухфазная сортировка – это сортировка, в которой отдельно реализуется две фазы: распределение и слияние.
Однофазная сортировка – это сортировка, в которой объединены фазы распределения и слияния в одну.
Двухпутевым слиянием называется сортировка, в которой данные распределяются на два вспомогательных файла.
Многопутевым слиянием называется сортировка, в которой данные распределяются на N (N > 2) вспомогательных файлов.

Общий алгоритм сортировки слиянием
Сначала серии распределяются на два или более вспомогательных файлов. Данное распределение идет поочередно: первая серия записывается в первый вспомогательный файл, вторая – во второй и так далее до последнего вспомогательного файла.
Затем опять запись серии начинается в первый вспомогательный файл. После распределения всех серий, они объединяются в более длинные упорядоченные отрезки, то есть из каждого вспомогательного файла берется по одной серии, которые сливаются.
Если в каком-то файле серия заканчивается, то переход к следующей серии не осуществляется. В зависимости от вида сортировки сформированная более длинная упорядоченная серия записывается либо в исходный файл, либо в один из вспомогательных файлов.
После того как все серии из всех вспомогательных файлов объединены в новые серии, потом опять начинается их распределение. И так до тех пор, пока все данные не будут отсортированы.
Основные характеристики сортировки слиянием:
количество фаз в реализации сортировки;
количество вспомогательных файлов, на которые распределяются серии.

Сортировка простым слиянием
Алгоритм сортировки простым слияния является простейшим алгоритмом внешней сортировки, основанный на процедуре слияния серией.
В данном алгоритме длина серий фиксируется на каждом шаге.
В исходном файле все серии имеют длину 1,
после первого шага она равна 2,
после второго – 4,
после третьего – 8,
после k-го шага – 2k.
Алгоритм сортировки простым слиянием
Шаг 1. Исходный файл f разбивается на два вспомогательных файла f1 и f2.
Шаг 2. Вспомогательные файлы f1 и f2 сливаются в файл f, при этом
одиночные элементы образуют упорядоченные пары.
Шаг 3. Полученный файл f вновь обрабатывается, как указано в шагах 1 и 2. При этом упорядоченные пары переходят в упорядоченные четверки.
Шаг 4. Повторяя шаги, сливаем четверки в восьмерки и т.д., каждый раз удваивая длину слитых последовательностей до тех пор, пока не будет упорядочен целиком весь файл.

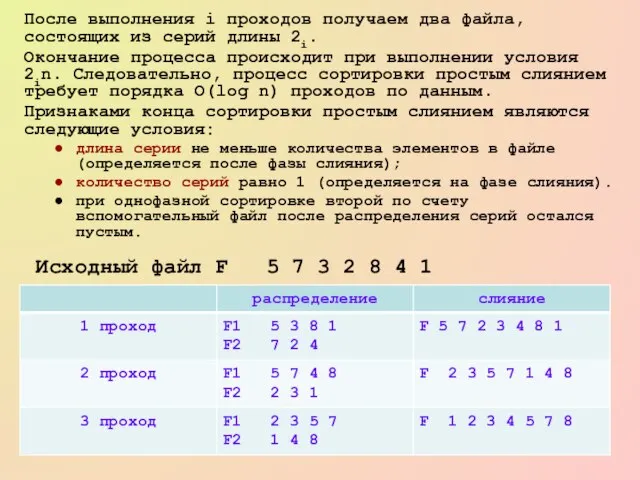
После выполнения i проходов получаем два файла, состоящих из серий длины 2i.
Окончание процесса происходит при выполнении условия 2in. Следовательно, процесс сортировки простым слиянием требует порядка O(log n) проходов по данным.
Признаками конца сортировки простым слиянием являются следующие условия:
длина серии не меньше количества элементов в файле (определяется после фазы слияния);
количество серий равно 1 (определяется на фазе слияния).
при однофазной сортировке второй по счету вспомогательный файл после распределения серий остался пустым.
Исходный файл F 5 7 3 2 8 4 1

//Описание функции сортировки простым слиянием
void Simple_Merging_Sort (char *name)
{
int a1, a2, k, i, j, kol, tmp;
FILE *f, *f1, *f2;
kol = 0;
if ( (f = fopen(name,"r")) == NULL )
cout<<"\nИсходный файл не может быть прочитан...";
else //если файл открыт
{
while ( !feof(f) ) //пока не конец файла
{
fscanf(f,"%d",&a1);
kol++; //количество элементов в файле f
}
fclose(f);
}//else
k = 1; //счётчик
while ( k < kol )
{
f = fopen(name,"r");
f1 = fopen("smsort_1","w");
f2 = fopen("smsort_2","w");
if ( !feof(f) ) fscanf(f,"%d",&a1);

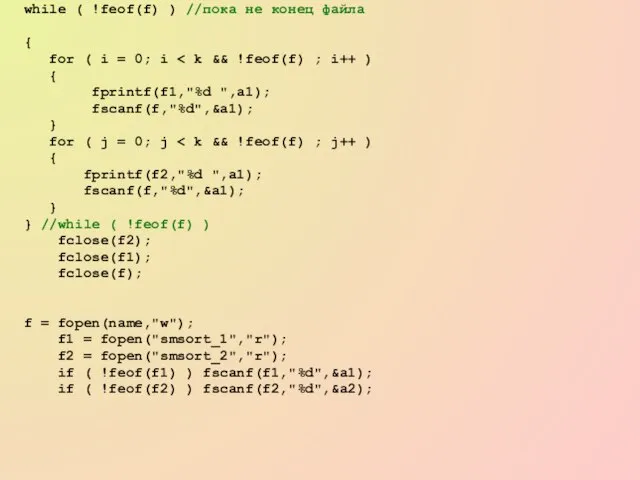
while ( !feof(f) ) //пока не конец файла
{
for ( i = 0; i < k && !feof(f) ; i++ )
{
fprintf(f1,"%d ",a1);
fscanf(f,"%d",&a1);
}
for ( j = 0; j < k && !feof(f) ; j++ )
{
fprintf(f2,"%d ",a1);
fscanf(f,"%d",&a1);
}
} //while ( !feof(f) )
fclose(f2);
fclose(f1);
fclose(f);
f = fopen(name,"w");
f1 = fopen("smsort_1","r");
f2 = fopen("smsort_2","r");
if ( !feof(f1) ) fscanf(f1,"%d",&a1);
if ( !feof(f2) ) fscanf(f2,"%d",&a2);

while( !feof(f1) && !feof(f2) )
{
i = 0;
j = 0;
while(i && j
{
if ( a1 < a2 )
{
fprintf(f,"%d ",a1);
fscanf(f1,"%d",&a1);
i++;
}
else
{
fprintf(f,"%d ",a2);
fscanf(f2,"%d",&a2);
j++;
}
}// while( i < k && j < k && //!feof(f1) && !feof(f2) )
while ( i < k && !feof(f1) )
{
fprintf(f,"%d ",a1);
fscanf(f1,"%d",&a1);
i++;
}
while ( j < k && !feof(f2) )
{
fprintf(f,"%d ",a2);
fscanf(f2,"%d",&a2);
j++;
}
} //while ( !feof(f1) && //!feof(f2) )

while ( !feof(f1) )
{
fprintf(f,"%d ",a1);
fscanf(f1,"%d",&a1);
}
while ( !feof(f2) )
{ fprintf(f,"%d ",a2);
fscanf(f2,"%d",&a2);
}
fclose(f2);
fclose(f1);
fclose(f);
k *= 2; //удвоить
}
remove("smsort_1");//удалить
remove("smsort_2");
}

Сортировка естественным слиянием
В случае простого слияния частичная упорядоченность сортируемых данных не дает никакого преимущества. Это объясняется тем, что на каждом проходе сливаются серии фиксированной длины.
При естественном слиянии длина серий не ограничивается, а определяется количеством элементов в уже упорядоченных подпоследовательностях, выделяемых на каждом проходе.
Сортировка, при которой всегда сливаются две самые длинные из возможных последовательностей, является естественным слиянием. В данной сортировке объединяются серии максимальной длины.

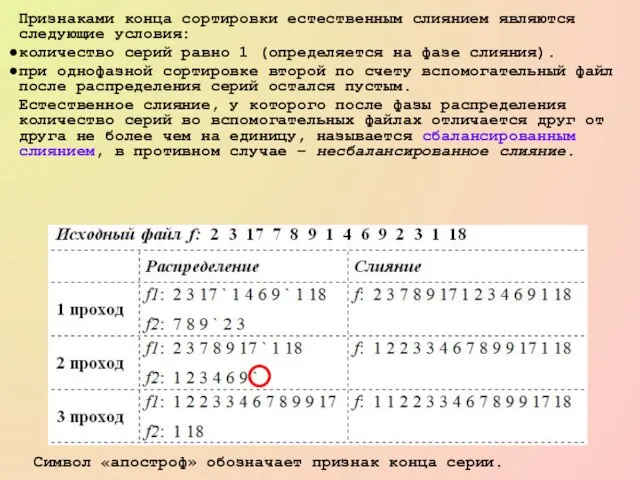
Алгоритм сортировки естественным слиянием
Шаг 1. Исходный файл f разбивается на два вспомогательных файла f1 и f2. Распределение происходит следующим образом:
поочередно считываются записи ai исходной последовательности (неупорядоченной) таким образом, что если значения ключей соседних записей удовлетворяют условию f(ai)f(ai+1), то они записываются в первый вспомогательный файл f1.
Как только встречаются f(ai)>f(ai+1), то записи ai+1 копируются во второй вспомогательный файл f2. Процедура повторяется до тех пор, пока все записи исходной последовательности не будут распределены по файлам.
Шаг 2.Вспомогательные файлы f1 и f2 сливаются в файл f,при этом серии образуют упорядоченные последовательности.
Шаг 3. Полученный файл f вновь обрабатывается, как указано в шагах 1 и 2.
Шаг 4. Повторяя шаги, сливаем упорядоченные серии до тех пор, пока не будет упорядочен целиком весь файл.

Признаками конца сортировки естественным слиянием являются следующие условия:
количество серий равно 1 (определяется на фазе слияния).
при однофазной сортировке второй по счету вспомогательный файл после распределения серий остался пустым.
Естественное слияние, у которого после фазы распределения количество серий во вспомогательных файлах отличается друг от друга не более чем на единицу, называется сбалансированным слиянием, в противном случае – несбалансированное слияние.
Символ «апостроф» обозначает признак конца серии.

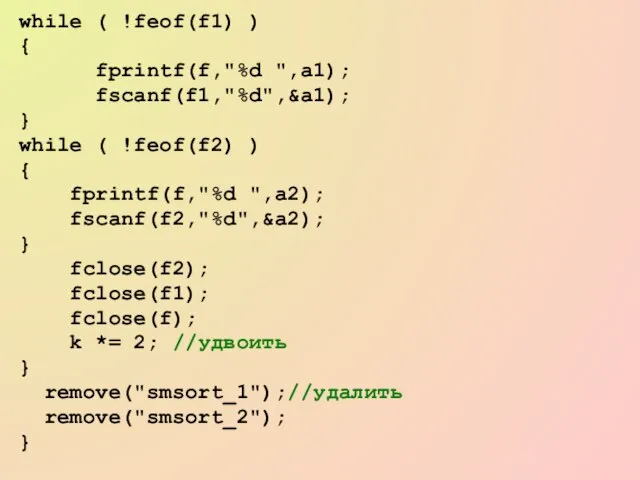
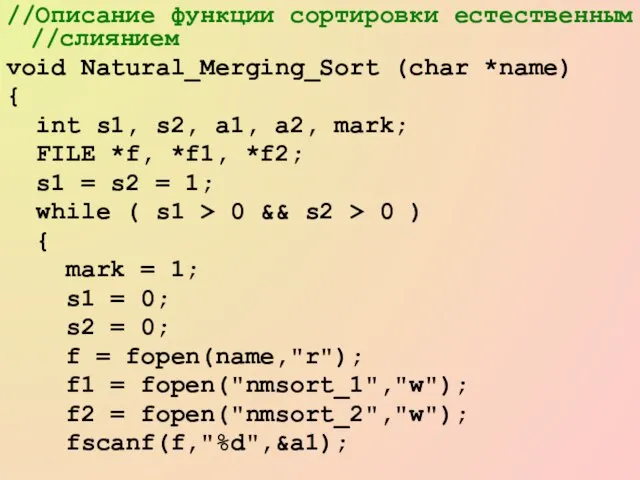
//Описание функции сортировки естественным //слиянием
void Natural_Merging_Sort (char *name)
{
int s1, s2, a1, a2, mark;
FILE *f, *f1, *f2;
s1 = s2 = 1;
while ( s1 > 0 && s2 > 0 )
{
mark = 1;
s1 = 0;
s2 = 0;
f = fopen(name,"r");
f1 = fopen("nmsort_1","w");
f2 = fopen("nmsort_2","w");
fscanf(f,"%d",&a1);

if ( !feof(f) ) { fprintf(f1,"%d ",a1); }
if ( !feof(f) ) fscanf(f,"%d",&a2);
while ( !feof(f) )
{
if ( a2 < a1 )
{ switch (mark)
{
case 1:{fprintf(f1,"' "); mark = 2; s1++; break;}
case 2:{fprintf(f2,"' "); mark = 1; s2++; break;}
}// switch
}//while ( !feof(f) )
if ( mark == 1 )
{ fprintf(f1,"%d ",a2); s1++; }
else { fprintf(f2,"%d ",a2); s2++;}
a1 = a2;
fscanf(f,"%d",&a2);
}//while ( s1 > 0 && s2 > 0 )

if ( s2 > 0 && mark == 2 )
{ fprintf(f2,"'");} if ( s1 > 0 && mark == 1 )
{ fprintf(f1,"'");}
fclose(f2);
fclose(f1);
fclose(f);
cout << endl;
Print_File(name);
Print_File("nmsort_1");
Print_File("nmsort_2");
cout << endl;
f = fopen(name,"w");
f1 = fopen("nmsort_1","r");
f2 = fopen("nmsort_2","r");
if ( !feof(f1) ) fscanf(f1,"%d",&a1);
if ( !feof(f2) ) fscanf(f2,"%d",&a2);

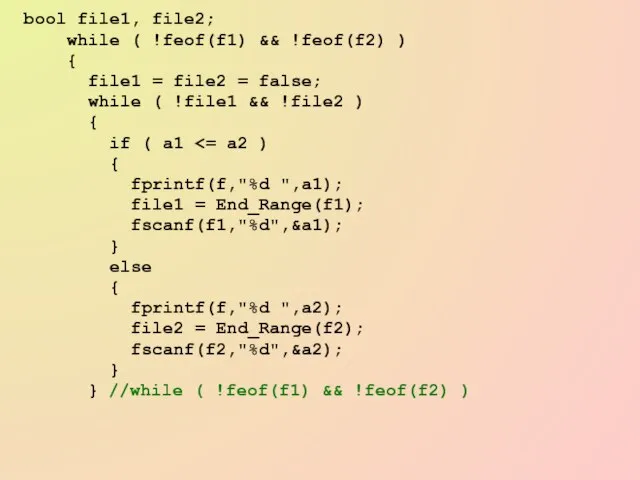
bool file1, file2;
while ( !feof(f1) && !feof(f2) )
{
file1 = file2 = false;
while ( !file1 && !file2 )
{
if ( a1 <= a2 )
{
fprintf(f,"%d ",a1);
file1 = End_Range(f1);
fscanf(f1,"%d",&a1);
}
else
{
fprintf(f,"%d ",a2);
file2 = End_Range(f2);
fscanf(f2,"%d",&a2);
}
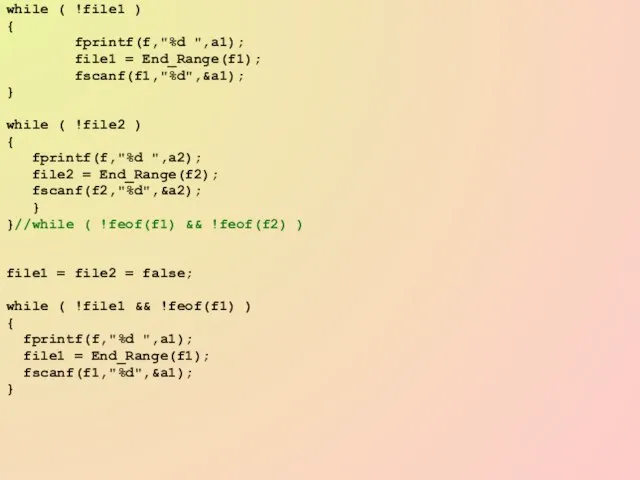
} //while ( !feof(f1) && !feof(f2) )

while ( !file1 )
{
fprintf(f,"%d ",a1);
file1 = End_Range(f1);
fscanf(f1,"%d",&a1);
}
while ( !file2 )
{
fprintf(f,"%d ",a2);
file2 = End_Range(f2);
fscanf(f2,"%d",&a2);
}
}//while ( !feof(f1) && !feof(f2) )
file1 = file2 = false;
while ( !file1 && !feof(f1) )
{
fprintf(f,"%d ",a1);
file1 = End_Range(f1);
fscanf(f1,"%d",&a1);
}

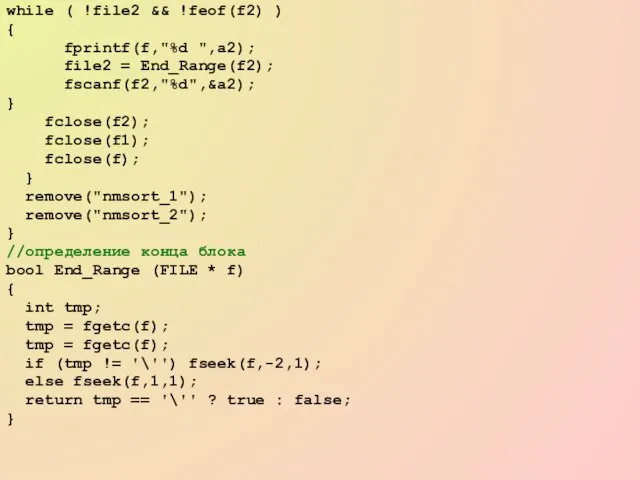
while ( !file2 && !feof(f2) )
{
fprintf(f,"%d ",a2);
file2 = End_Range(f2); fscanf(f2,"%d",&a2);
}
fclose(f2);
fclose(f1);
fclose(f);
}
remove("nmsort_1");
remove("nmsort_2");
}
//определение конца блока
bool End_Range (FILE * f)
{
int tmp;
tmp = fgetc(f);
tmp = fgetc(f);
if (tmp != '\'') fseek(f,-2,1);
else fseek(f,1,1);
return tmp == '\'' ? true : false;
}

Выводы.
Число чтений или перезаписей файлов при использовании метода естественного слияния будет не хуже, чем при применении метода простого слияния, а в среднем – даже лучше.
Но в этом методе увеличивается число сравнений за счет тех, которые требуются для распознавания концов серий.
Помимо этого, максимальный размер вспомогательных файлов может быть близок к размеру исходного файла, т.к. длина серий может быть произвольной.

Краткие итоги
Внешние сортировки применяются к данным, которые хранятся во внешней памяти.
Внешние сортировки применяются, если объем сортируемых данных превосходит допустимое место в ОЗУ.
Внешние сортировки, по сравнению с внутренними, характеризуются проигрышем по времени за счет обращения к внешним носителям.
К наиболее известным алгоритмам внешних сортировок относятся:
?сортировки слиянием (простое слияние и естественное слияние);
? улучшенные сортировки (многофазная сортировка и каскадная сортировка).

Алгоритмы внешних сортировок отличаются по реализации числом фаз и путей.
Простое слияние является одной из сортировок на основе слияния, в которой длина серий фиксируется на каждом шаге.
Естественное слияние является сортировкой, при которой всегда сливаются две самые длинные из возможных серий.
Число чтений или перезаписей файлов при использовании метода естественного слияния будет не хуже, чем при применении метода простого слияния, а в среднем – даже лучше. Однако в данном методе увеличивается число сравнений за счет распознавания концов серий.