Содержание
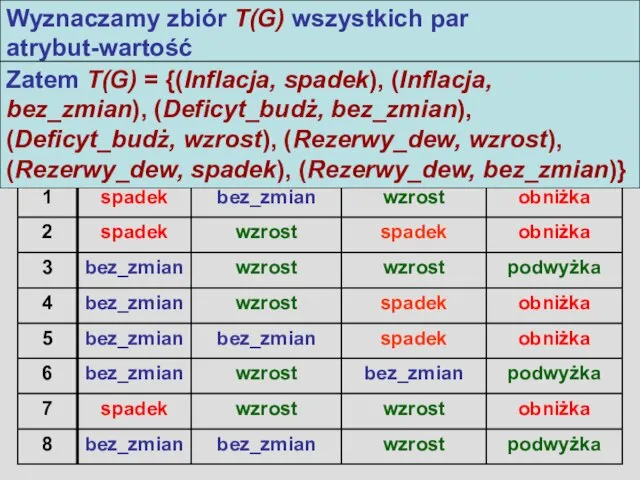
- 2. Algorytm LEM2 Wyznaczamy zbiór T(G) wszystkich par atrybut-wartość Zatem T(G) = {(Inflacja, spadek), (Inflacja, bez_zmian), (Deficyt_budż,
- 3. Algorytm LEM2 [(Inflacja, spadek)] = {1, 2, 7} [(Inflacja, bez_zmian)] = {3, 4, 5, 6, 8}
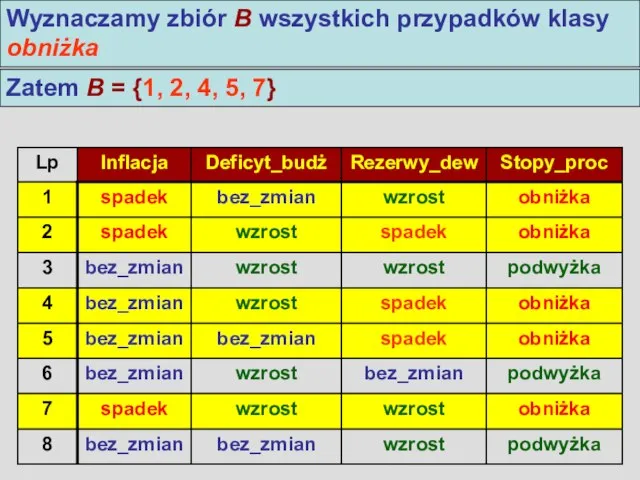
- 4. Algorytm LEM2 Wyznaczamy zbiór B wszystkich przypadków klasy obniżka Zatem B = {1, 2, 4, 5,
- 5. Algorytm LEM2 Wyznaczamy zbiór B wszystkich przypadków klasy obniżka Zatem B = {1, 2, 4, 5,
- 6. Zakładamy wstępnie, że G = B = {1, 2, 4, 5, 7} oraz T = Ø
- 7. [(Inflacja, spadek)] = {1, 2, 7} ⊆ B T = Ø ∪ {(Inflacja, spadek)} = {(Inflacja,
- 8. Spośród wszystkich par atrybut-wartość wybieramy: parę która ma największe przecięcie ze zbiorem G max|[t] ∩ G]|
- 9. [(Rezerwy_dew, spadek)] = {2, 4, 5} ⊆ B [T] = {1, 2, 7} ∪ {2, 4,
- 10. Ponieważ G = Ø zatem powyższe reguły pokrywają wszystkie przypadki z kategorii obniżka, teraz należy znaleźć
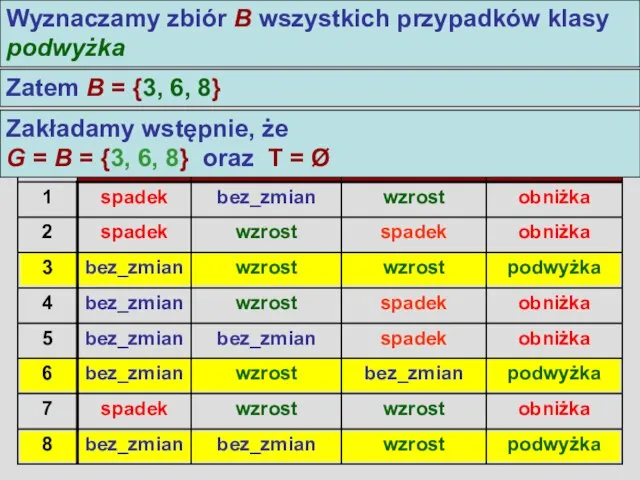
- 11. Algorytm LEM2 Wyznaczamy zbiór B wszystkich przypadków klasy podwyżka Zatem B = {3, 6, 8} Zakładamy
- 12. Spośród wszystkich par atrybut-wartość wybieramy: parę która ma największe przecięcie ze zbiorem G max|[t] ∩ G]|
- 13. [(Inflacja, bez_zmian)] = {3, 4, 5, 6, 8} [(Deficyt_budż, bez_zmian)] = {1, 5, 8} [(Deficyt_budż, wzrost)]
- 14. T = {(Inflacja, bez_zmian), (Rezerwy_dew, wzrost)} for each t ∈ T do if [T – {t}]
- 15. Reguła 3: JEŻELI Inflacja JEST bez_zmian ORAZ Rezerwy_dew JEST wzrost TO Stopy_proc JEST podwyżka [T] =
- 16. G = B – [T] = {3, 6, 8} – {3, 8} = {6} [(Deficyt_budż, bez_zmian)]
- 17. Reguła 1: JEŻELI Inflacja JEST spadek TO Stopy_proc JEST obnizka Reguła 2: JEŻELI Rezerwy_dew JEST spadek
- 19. Скачать презентацию
![Algorytm LEM2 [(Inflacja, spadek)] = {1, 2, 7} [(Inflacja, bez_zmian)] = {3,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/849421/slide-2.jpg)


![[(Inflacja, spadek)] = {1, 2, 7} ⊆ B T = Ø ∪](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/849421/slide-6.jpg)

![[(Rezerwy_dew, spadek)] = {2, 4, 5} ⊆ B [T] = {1, 2,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/849421/slide-8.jpg)


![[(Inflacja, bez_zmian)] = {3, 4, 5, 6, 8} [(Deficyt_budż, bez_zmian)] = {1,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/849421/slide-12.jpg)


![G = B – [T] = {3, 6, 8} – {3, 8}](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/849421/slide-15.jpg)

 Стилизация человека
Стилизация человека Евро - валюта Европейских стран
Евро - валюта Европейских стран Общее устройство тормозной системы автомобилей
Общее устройство тормозной системы автомобилей Изменение имён прилагательных по родам и числам 3 класс
Изменение имён прилагательных по родам и числам 3 класс Коммуникативный акт
Коммуникативный акт Космические дали в Перми
Космические дали в Перми Тема текста
Тема текста Конкурс болельщиков
Конкурс болельщиков Сибирский специалитет. Промо – дегустация
Сибирский специалитет. Промо – дегустация О результатах внедрения федеральных государственных требований к структуре основной общеобразовательной программы дошкольного
О результатах внедрения федеральных государственных требований к структуре основной общеобразовательной программы дошкольного  Общее представление о строении металлов
Общее представление о строении металлов Презентация на тему Корней Иванович Чуковский
Презентация на тему Корней Иванович Чуковский «Четвертый канал» «Четвертый канал» - это первая независимая негосударственная телекомпания Екатеринбурга. Наша работа отмечена
«Четвертый канал» «Четвертый канал» - это первая независимая негосударственная телекомпания Екатеринбурга. Наша работа отмечена  Технология распознавания движения Move assistant
Технология распознавания движения Move assistant Микропроцессоры
Микропроцессоры Интерьер как художественно-архитектурная среда и жанр изобразительного искусства. 7 класс
Интерьер как художественно-архитектурная среда и жанр изобразительного искусства. 7 класс Температура воздуха
Температура воздуха Искусство и я (4 класс)
Искусство и я (4 класс) Уникальные животные Тувы
Уникальные животные Тувы Темы 2.1 и 2.2. Организация и схема проведения внешнеэкономической операции при прямых и косвенных связях между контрагентами. Орган
Темы 2.1 и 2.2. Организация и схема проведения внешнеэкономической операции при прямых и косвенных связях между контрагентами. Орган Праздники, традиции, обычаи народов мира
Праздники, традиции, обычаи народов мира Отчет по практике по получению профессиональных навыков
Отчет по практике по получению профессиональных навыков Нанесение пленок нафтоноата европия методом разнолигандного комплексообразования и разложения
Нанесение пленок нафтоноата европия методом разнолигандного комплексообразования и разложения Концертный зал Измайлово ____________________________.
Концертный зал Измайлово ____________________________. Предзаказы на 8 марта. Шашлычная
Предзаказы на 8 марта. Шашлычная Алгоритмы сортировки массивов.
Алгоритмы сортировки массивов. Безопасность на водных объектах
Безопасность на водных объектах Информационные модели 6-7 класс
Информационные модели 6-7 класс