Аналитико-систематическая исследовательская работа на тему:“Удивительная симметрия”

Цели:
-рассмотреть виды и типы симметрий;
-проанализировать как и где используется симметрия;
-рассмотреть, как симметрия используется в школьном курсе алгебры
Задачи:
- Прочитать соответствующую литературу;
- Узнать, как понимали симметрию древнейшие учёные;
- Познакомиться с основными видами симметрии и использованием их в различных областях жизни и деятельности человека;
- Рассмотреть примеры применения симметрии в архитектуре, искусстве, музыке и в алгебре

Симметрия…является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.
Г. Вейль

Аспекты, без которых симметрия невозможна:
1) объект - носитель симметрии; в роли симметричных объектов могут выступать вещи, процессы, геометрические фигуры, математические выражения, живые организмы и т.д.
2) некоторые признаки - величины, свойства, отношения, процессы, явления - объекта, которые при преобразованиях симметрии остаются неизменными; их называют инвариантными или инвариантами.
3)изменения (объекта), которые оставляют объект тождественным самому себе по инвариантным признакам; такие изменения называются преобразованиями симметрии;
4) свойство объекта превращаться по выделенным признакам в самого себя после соответствующих его изменений.

Асимметрия - отсутствие или нарушение симметрии.
Диссимметрия - нарушенная,частично расстроенная симметрия

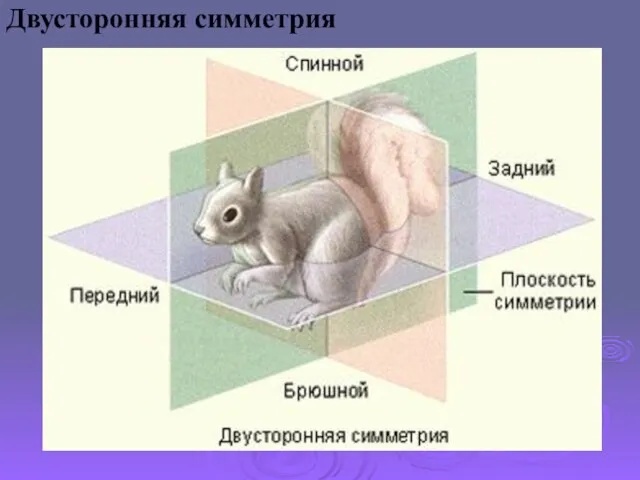
Двусторонняя симметрия

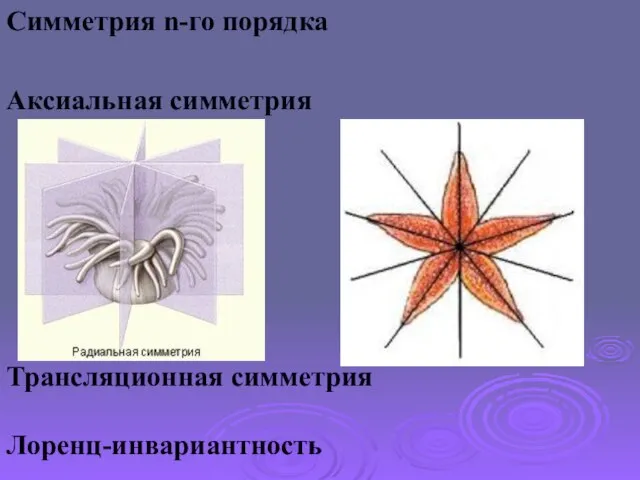
Симметрия n-го порядка
Аксиальная симметрия
Трансляционная симметрия
Лоренц-инвариантность

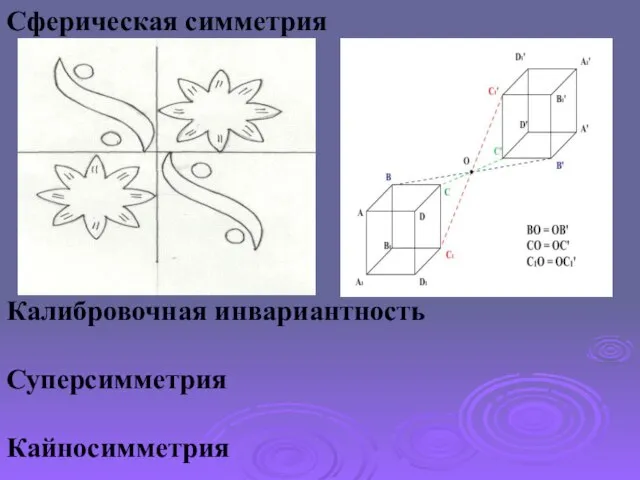
Сферическая симметрия
Калибровочная инвариантность
Суперсимметрия
Кайносимметрия

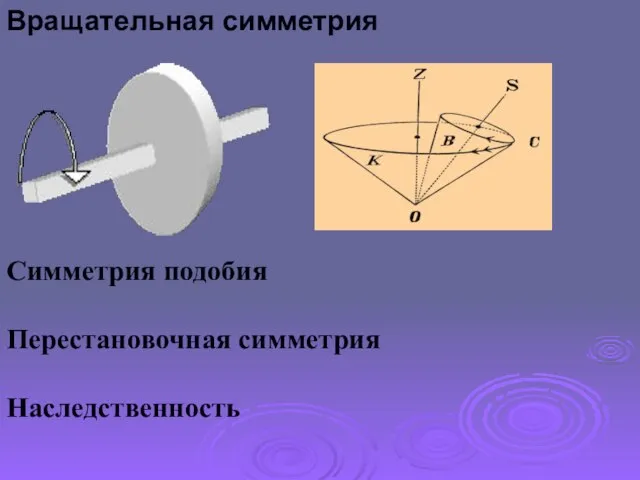
Вращательная симметрия
Симметрия подобия
Перестановочная симметрия
Наследственность

Симметрия у животных и человека.

Симметрия в искусстве

Симметрия в архитектуре

Симметрия в музыке

Симметрия в алгебре.
Симметрические выражения.
Рассмотрим выражение с двумя переменными
Если в каждом из них переставим переменные, то есть всюду вместо
поставим
, и вместо
поставим
то получим тождественно равные им выражения:
Такие выражения называются симметрическим относительно этих переменных.

Решение симметрических систем уравнений.
Если оба уравнения системы являются симметрическими многочленами от
и
, то систему уравнений называют симметрической системой уравнений.
Использование симметрии при решении задач.
Решения многих задач значительно упрощаются, если использовать симметрию.

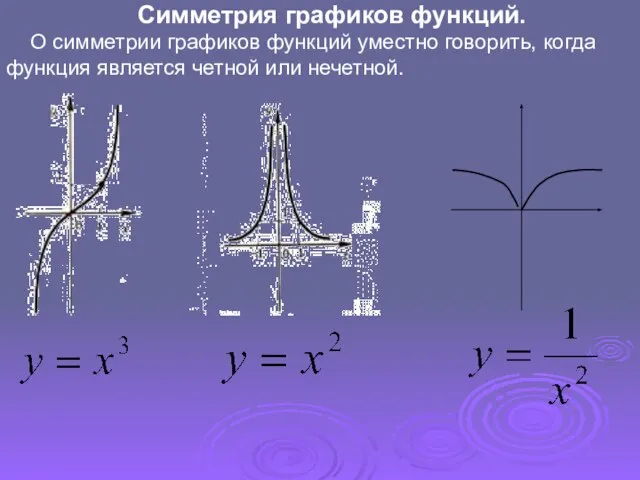
Симметрия графиков функций.
О симметрии графиков функций уместно говорить, когда функция является четной или нечетной.