- Главная
- Разное
- АНАЛИЗ БЕЗОПАСНОСТИ УПРАВЛЕНИЯ ДОСТУПОМ И ИНФОРМАЦИОННЫМИ ПОТОКАМИ В КОМПЬЮТЕРНЫХ СИСТЕМАХ

Содержание
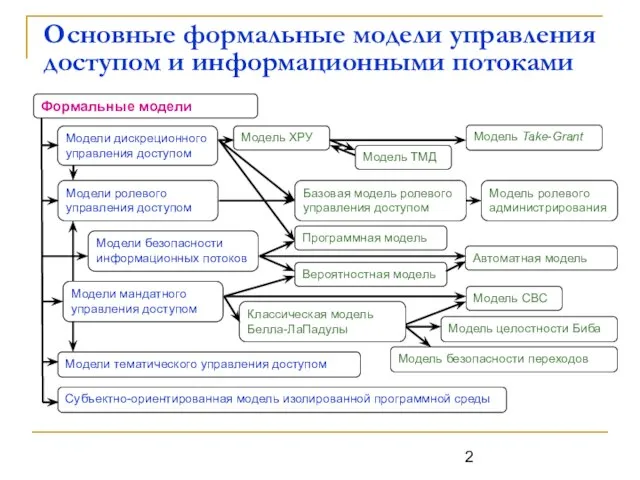
- 2. Основные формальные модели управления доступом и информационными потоками
- 3. Основные существенные особенности функционирования современных КС Возможность реализации в КС доверенных и недоверенных субъектов с различными
- 4. Критический анализ основных формальных моделей
- 5. Предположение 1. Все действия в КС, в том числе выполнение операций над сущностями, порождение информационных потоков,
- 6. Базовая ДП-модель. Иерархия сущностей E = O ∪ C ⎯ множество сущностей, где O ⎯ множество
- 7. Определение. Пусть определены множества S, E, R ⊆ S × E × Rr, A ⊆ S
- 8. Правила преобразования состояний В базовой ДП-модели определены 16 монотонных и немонотонных правил преобразования состояний: take_right(αr, x,
- 9. Примеры правил преобразования состояний базовой ДП-модели
- 10. Условия передачи прав доступа или реализации информационных потоков Определение. Пусть G0 = (S0, E0, R0 ∪
- 11. Условия реализации информационного потока по времени Теорема. Пусть G0 = (S0, E0, R0 ∪ A0 ∪
- 12. Фрагменты доказательства теоремы Пример задачи на преобразование графа доступов расширенной модели Take-Grant
- 13. Фрагменты доказательства теоремы Докажем достаточность выполнения условия теоремы для истинности предиката can_write_time(x, y, G0). … Пусть
- 14. Фрагменты доказательства теоремы Докажем необходимость выполнения условия теоремы для истинности предиката can_write_time(x, y, G0). Пусть истинен
- 15. ДП-модель без кооперации доверенных и недоверенных субъектов Определение. Назовем траекторию функционирования системы Σ(G*, OP) траекторией без
- 16. Правила преобразования состояний Предположение. Доверенные субъекты системы Σ(G*, OP) не участвуют в реализации информационных потоков по
- 17. ДП-модель с блокирующими доступами доверенных субъектов
- 18. ДП-модель с блокирующими доступами доверенных субъектов Предположение. Блокирующие доступы доверенных субъектов к сущностям системы Σ(G*, OP)
- 19. Теорема. Пусть G0 = (S0, E0, R0 ∪ A0 ∪ F0, HB0) ⎯ состояние системы Σ(G*,
- 20. Метод предотвращения запрещенных информационных потоков по времени Метод 1. Условие применения метода. Пусть определена система Σ(G*,
- 21. ДП-модель с функционально ассоциированными с субъектами сущностями
- 22. ДП-модель с функционально ассоциированными с субъектами сущностями Определение. Доверенного субъекта y назовем функционально корректным, если во
- 23. ДП-модель для политики безопасного администрирования Определение. В политике безопасного администрирования рассматриваются две угрозы безопасности КС. Угроза
- 24. ДП-модель для политики абсолютного разделения административных и пользовательских полномочий Определение. Для системы Σ(G*, OP) рассматриваются два
- 25. Методы предотвращения возможности получения права доступа владения Метод предотвращения возможности получения права доступа владения недоверенным субъектом
- 26. Мандатная ДП-модель. Виды запрещенных информационных потоков Определение. Определим как запрещенные в КС с мандатным управлением доступом
- 27. Мандатная ДП-модель. Основные определения (L, ≤) ⎯ решетка линейно упорядоченных уровней доступа и конфиденциальности; ES ⊂
- 28. Мандатная ДП-модель. Правила преобразования состояний
- 29. Условия несанкционированного повышения уровня доступа субъекта Теорема. Пусть уровень доступа l ∈ L и G0 =
- 30. Информационные потоки по времени
- 31. Мандатные ДП-модели Мандатная ДП-модель с блокирующими доступами доверенных субъектов; ДП-модель с отождествлением порожденных субъектов (в системе
- 32. Метод предотвращения возможности реализации запрещенных информационных потоков по времени Метод. Условие применения метода. Пусть определена система
- 33. Семейство ДП-моделей
- 35. Скачать презентацию
Слайд 3Основные существенные особенности функционирования современных КС
Возможность реализации в КС доверенных и недоверенных
Основные существенные особенности функционирования современных КС
Возможность реализации в КС доверенных и недоверенных

Различие в условиях реализации в КС информационных потоков по памяти и по времени;
Наличие в современных КС иерархической структуры сущностей и возможность ее использования при реализации информационных потоков по времени;
Возможность кооперации или, наоборот, противодействия субъектов друг другу при передаче прав доступа и реализации информационных потоков.
Возможность изменения функциональности субъекта при реализации информационного потока по памяти на функционально ассоциированные с ним сущности.
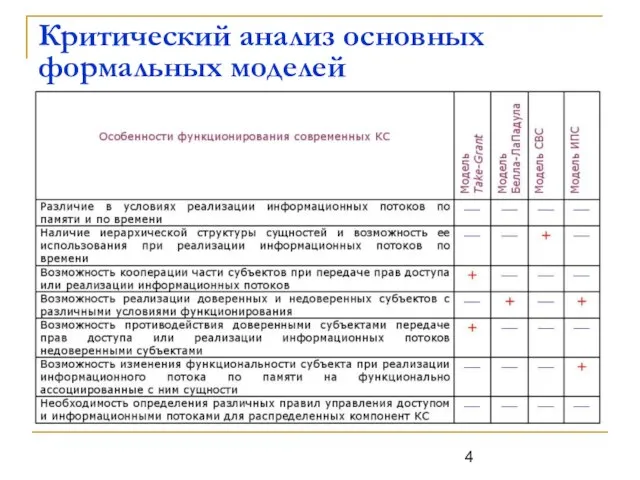
Слайд 4Критический анализ основных формальных моделей
Критический анализ основных формальных моделей
Слайд 5Предположение 1. Все действия в КС, в том числе выполнение операций над
Предположение 1. Все действия в КС, в том числе выполнение операций над

Предположение 2. Все информационные потоки в КС порождены доступами субъектов к сущностям. Иные информационные потоки, например по побочному электромагнитному излучению, не рассматриваются.
Предположение 3. В начальном состоянии КС отсутствуют доступы субъектов к объектам и информационные потоки.
Предположение 4. При любых запросе субъекта на доступ к сущности или доступе субъекта к сущности реализуется информационный поток по времени.
Предположение 5. При реализации информационного потока по памяти от объекта-источника к объекту-приемнику в том же направлении реализуется информационный поток по времени.
Основные предположения
Слайд 6Базовая ДП-модель.
Иерархия сущностей
E = O ∪ C ⎯ множество сущностей, где
Базовая ДП-модель.
Иерархия сущностей
E = O ∪ C ⎯ множество сущностей, где

Rr = {readr, writer, appendr, executer, ownr} ⎯ множество видов прав доступа;
Ra = {reada, writea, appenda} ⎯ множество видов доступа;
Rf = {writem, writet} ⎯ множество видов информационных потоков;
Rraf = Rr ∪ Ra ∪ Rf ⎯ множество видов прав доступа, видов доступа и видов информационных потоков.
Определение. Определим H: E → 2E ⎯ функцию иерархии сущностей, сопоставляющую каждой сущности c ∈ E множество сущностей H(c) ⊂ E и удовлетворяющую условиям:
Условие 1. Если сущность e ∈ H(c), то e < c и не существует сущности-контейнера d ∈ C, такой, что e < d, d < c.
Условие 2. Для любых сущностей e1, e2 ∈ E, e1 ≠ e2, по определению выполняются равенство H(e1) ∩ H(e2) = ∅ и условия:
если o ∈ O, то выполняется равенство H(o) = ∅;
если e1 < e2, то или e1, e2 ∈ E \ S, или e1, e2 ∈ S;
если e ∈ E \ S, то H(e) ⊂ E \ S;
если s ∈ S, то H(s) ⊂ S.
Слайд 7Определение. Пусть определены множества S, E, R ⊆ S × E ×
Определение. Пусть определены множества S, E, R ⊆ S × E ×

Σ(G*, OP) ⎯ система, при этом:
каждое состояние системы представляется графом доступов;
G* ⎯ множество всех возможных состояний;
OP ⎯ множество правил преобразования состояний;
G ├ op G’ ⎯ переход системы Σ(G*, OP) из состояния G в состояние G’
Определение системы
Слайд 8Правила преобразования состояний
В базовой ДП-модели определены 16 монотонных и немонотонных правил преобразования
Правила преобразования состояний
В базовой ДП-модели определены 16 монотонных и немонотонных правил преобразования

Слайд 9Примеры правил преобразования состояний базовой ДП-модели
Примеры правил преобразования состояний базовой ДП-модели

Слайд 10Условия передачи прав доступа или реализации информационных потоков
Определение. Пусть G0 = (S0,
Условия передачи прав доступа или реализации информационных потоков
Определение. Пусть G0 = (S0,

Определение. Пусть G0 = (S0, E0, R0 ∪ A0 ∪ F0, H0) ⎯ состояние системы Σ(G*, OP) и сущности x, y ∈ E0, где x ≠ y. Определим предикат can_write_memory(x, y, G0), который будет истинным тогда, и только тогда, когда существуют состояния G1, …, GN = (SN, EN, RN ∪ AN ∪ FN, HN) и правила преобразования состояний op1, …, opN такие, что G0 ├ op1 G1 ├ op2 … ├ opN GN и (x, y, writem) ∈ FN, где N ≥ 0.
Определение. Пусть G0 = (S0, E0, R0 ∪ A0 ∪ F0, H0) ⎯ состояние системы Σ(G*, OP) и сущности x, y ∈ E0, где x ≠ y. Определим предикат can_write_time(x, y, G0), который будет истинным тогда, и только тогда, когда существуют состояния G1, …, GN = (SN, EN, RN ∪ AN ∪ FN, HN) и правила преобразования состояний op1, …, opN такие, что G0 ├ op1 G1 ├ op2 … ├ opN GN и (x, y, αf) ∈ FN, где αf ∈ {writem, writet} и N ≥ 0.
Слайд 11Условия реализации информационного потока по времени
Теорема. Пусть G0 = (S0, E0,
Условия реализации информационного потока по времени
Теорема. Пусть G0 = (S0, E0,

Условие 1. m = 2 и (x, y, αf) ∈ F0, где αf ∈ {writem, writet}.
Условие 2. Для каждого i = 1, ..., m – 1 выполняется одно из условий:
ei ∈ S0 и (ei, ei + 1, writet) ∈ F0;
ei ∈ S0 и истинен предикат can_write_memory(ei, ei + 1, G0);
ei ∈ S0 и существует сущность e’i + 1 ∈ E0, такая, что e’i + 1 ≤ ei + 1 и истинен предикат can_share(αr, ei, e’i + 1, G0), αr ∈ Rr;
ei + 1 ∈ S0 и истинен предикат can_share(readr, ei + 1, ei, G0);
ei, ei + 1 ∈ S0 и существуют сущности e’i, e’i + 1 ∈ E0: или e’i ≤ e’i + 1, или e’i + 1 ≤ e’i, и истинны предикаты can_share(αr, ei, e’i, G0) и can_share(βr, ei + 1, e’i + 1, G0), αr, βr ∈ Rr.
Слайд 12Фрагменты доказательства теоремы
Пример задачи на преобразование графа доступов расширенной модели Take-Grant
Фрагменты доказательства теоремы
Пример задачи на преобразование графа доступов расширенной модели Take-Grant

Слайд 13Фрагменты доказательства теоремы
Докажем достаточность выполнения условия теоремы для истинности предиката can_write_time(x,
Фрагменты доказательства теоремы
Докажем достаточность выполнения условия теоремы для истинности предиката can_write_time(x,

…
Пусть выполняется условие 2 теоремы, тогда существует последовательность сущностей e1, …, em ∈ E0, где e1 = x, em = y и m ≥ 2. Выполним доказательство индукцией по длине m последовательности сущностей.
Пусть m = 2. Возможны пять случаев.
…
Рассмотрим четвертый случай: x ∈ S0 и существует сущность y’ ∈ E0, такая, что y’ ≤ y и истинен предикат can_share(αr, x, y’, G0), где αr ∈ Rr. Так как истинен предикат can_share(αr, x, y’, G0), то существуют состояния G1, …, GN = (SN, EN, RN ∪ AN ∪ FN, HN) и правила преобразования состояний op1, …, opN такие, что G0 ├ op1 G1 ├ op2 … ├ opN GN и (x, y’, αr) ∈ RN, где N ≥ 0.
Если αr ∈ {writer, appendr, readr}, то пусть opN + 1 = access_α(x, y’) и GN ├ op(N + 1) GN + 1, где GN + 1 = (SN + 1, EN + 1, RN + 1 ∪ AN + 1 ∪ FN + 1, HN + 1). Тогда (x, y, writet) ∈ FN + 1 и предикат can_write_time(x, y, G0) истинен.
Если αr = ownr, то пусть opN + 1 = own_take(writer, x, y’), opN + 2 = access_write(x, y’) и GN ├ op(N + 1) GN + 1 ├ op(N + 2) GN + 2, где GN + 2 = (SN + 2, EN + 2, RN + 2 ∪ AN + 2 ∪ FN + 2, HN + 2). Тогда (x, y, writet) ∈ FN + 2 и предикат can_write_time(x, y, G0) истинен.
Если αr = executer, то пусть opN + 1 = create_subject(x, y’, z) и GN ├ op(N + 1) GN + 1, где GN + 1 = (SN + 1, EN + 1, RN + 1 ∪ AN + 1 ∪ FN + 1, HN + 1) и z ∉ SN. Тогда (x, y, writet) ∈ FN+1 и предикат can_write_time(x, y, G0) истинен.
Слайд 14Фрагменты доказательства теоремы
Докажем необходимость выполнения условия теоремы для истинности предиката can_write_time(x,
Фрагменты доказательства теоремы
Докажем необходимость выполнения условия теоремы для истинности предиката can_write_time(x,

Пусть истинен предикат can_write_time(x, y, G0), при этом по определению существуют состояния G1, …, GN = (SN, EN, RN ∪ AN ∪ FN, HN) и правила преобразования состояний op1, …, opN такие, что G0 ├ op1 G1 ├ op2 … ├ opN GN и (x, y, αf) ∈ FN, где αf ∈ {writem, writet} и N ≥ 0. Среди всех таких последовательностей выберем ту, у которой длина N является минимальной. В этом случае (x, y, αf) ∉ FN – 1. Проведем доказательство индукцией по длине N последовательности преобразований.
Пусть N = 1, тогда (x, y, αf) ∉ F0 и существует правило преобразования состояний op1, такое, что G0 ├ op1 G1 и (x, y, αf) ∈ F1. Из определения правил преобразования состояний следует, что возможны девять случаев:
x, y ∈ S0, (x, y, ownr) ∈ R0;
x, y ∈ S0, (y, x, ownr) ∈ R0;
x ∈ S0, y ∈ E0 и существует сущность y’ ∈ E0, такая, что y’ ≤ y и (x, y’, αr) ∈ R0, при этом αr ∈ {readr, writer, appendr};
x, y ∈ S0 и существуют сущности x’, y’ ∈ E0, такие, что или x’ ≤ y’, или y’ ≤ x’ и {(x, x’, αr), {(y, y’, βr)} ⊂ R0, где αr, βr ∈ Rr;
y ∈ S0, x ∈ E0, (y, x, readr) ∈ R0;
x ∈ S0, y ∈ E0, (x, y, αr) ∈ R0, где αr ∈ {writer, appendr};
x ∈ S0, y ∈ E0 и существует сущность e ∈ E0, такая, что {(x, e, α), (e, y, β)} ⊂ R0 ∪ F0, где α, β ∈ {writer, appendr, writem, writet};
x, y ∈ S0 и существуют сущность e ∈ E0, такая, что {(x, e, α), (y, e, readr)} ⊂ R0 ∪ F0, где α ∈ {writer, appendr, writem, writet};
x, y ∈ E0 и существует субъект e ∈ S0, такой, что {(e, x, readr), (e, y, α)} ⊂ R0 ∪ F0, где α ∈ {writer, appendr, writem, writet}.
Слайд 15ДП-модель без кооперации доверенных и недоверенных субъектов
Определение. Назовем траекторию функционирования системы Σ(G*,
ДП-модель без кооперации доверенных и недоверенных субъектов
Определение. Назовем траекторию функционирования системы Σ(G*,

не дают недоверенным субъектам права доступа к сущностям;
не берут у недоверенных субъектов права доступа к сущностям.
Определение. Назовем траекторию функционирования системы Σ(G*, OP) траекторией без кооперации доверенных и недоверенных субъектов для передачи прав доступа и реализации информационных потоков, если она является траекторий без кооперации доверенных и недоверенных субъектов для передачи прав доступа и при ее реализации используются правила преобразования состояний:
take_right(αr, x, y, z), grant_right(αr, x, y, z), own_take(αr, x, y, z) с условиями и результатами применения определенными в рамках базовой ДП-модели;
create_entity(x, y, z), create_subject(x, y, z), rename_entity(x, y, z), access_read(x, y), access_write(x, y), access_append(x, y), flow(x, y, y’, z), find(x, y, z), post(x, y, z), pass(x, y, z) с условиями и результатами применения определенными в рамках ДП-модели без кооперации доверенных и недоверенных субъектов.
Слайд 16Правила преобразования состояний
Предположение. Доверенные субъекты системы Σ(G*, OP) не участвуют в реализации
Правила преобразования состояний
Предположение. Доверенные субъекты системы Σ(G*, OP) не участвуют в реализации

Слайд 17ДП-модель с блокирующими доступами доверенных субъектов
ДП-модель с блокирующими доступами доверенных субъектов
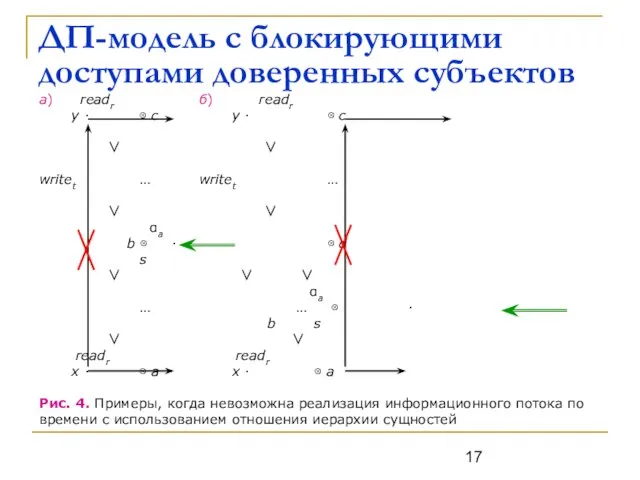
Слайд 18ДП-модель с блокирующими доступами доверенных субъектов
Предположение. Блокирующие доступы доверенных субъектов к
ДП-модель с блокирующими доступами доверенных субъектов
Предположение. Блокирующие доступы доверенных субъектов к

Определение. Иерархией сущностей с учетом блокирующих доступов доверенных субъектов называется заданное на множестве сущностей E отношение частичного порядка «≤B», удовлетворяющее условиям:
для двух сущностей e1, e2 ∈ E если выполняется неравенство e1 ≤B e2, то выполняется неравенство e1 ≤ e2;
если сущность e1 ∈ EB, то выполняется равенство {e ∈ E: e ≤B e1 или e1 ≤B e} = {e1} (каждая сущность из EB сравнима только сама с собой);
если для сущности e1 ∈ E существует сущность e2 ∈ EB, такая, что выполняется условие e2 ≤ e1, то выполняется равенство {e ∈ E: e ≤B e1 или e1 ≤B e} = {e1};
если для сущности e ∈ E существуют сущности e1, e2 ∈ E, такие, что e ≤B e2, e ≤B e1, то или e1 ≤B e2, или e2 ≤B e1.
В случае, когда для двух сущностей e1, e2 ∈ E выполняются условия e1, e2 ∈ E \ EB, e1 ≤B e2 и e1 ≠ e2, будем использовать обозначение: e1 Определение. Определим HB: E → 2E ⎯ функцию иерархии сущностей с учетом блокирующих доступов доверенных субъектов, сопоставляющую каждой сущности c ∈ E множество сущностей HB(c) ⊂ H(c), удовлетворяющих условию HB(c) = {e ∈ H(c): e
Слайд 19Теорема. Пусть G0 = (S0, E0, R0 ∪ A0 ∪ F0, HB0)
Теорема. Пусть G0 = (S0, E0, R0 ∪ A0 ∪ F0, HB0)

Условие 1. В состоянии G0 реализован информационный поток (x, y, αf) ∈ F0, где αf ∈ {writem, writet}.
Условие 2. Существует последовательность сущностей e1, …, em ∈ E0, где e1 = x, em = y и m ≥ 2, таких, что для каждого i = 1, ..., m – 1 выполняется одно из условий:
ei ∈ NS ∩ S0 и или (ei, ei + 1, αf) ∈ F0, где αf ∈ {writem, writet}, или истинен предикат can_share(αr, ei, ei + 1, G0, LS), где αr ∈ {writer, appendr};
ei ∈ NS ∩ S0, ei + 1 ∈ E0 \ EB и существует сущность e’i + 1 ∈ E0 \ EB, такая, что e’i + 1 ≤B ei + 1, и истинен предикат can_share(αr, ei, e’i + 1, G0, LS), где αr ∈ Rr;
ei + 1 ∈ NS ∩ S0 и истинен предикат can_share(readr, ei + 1, ei, G0, LS);
ei, ei + 1 ∈ NS ∩ S0 и существуют сущности e’i, e’i + 1 ∈ E0 \ EB, такие, что или e’i ≤B e’i + 1, или e’i + 1 ≤B e’i, и истинны предикаты can_share(αr, ei, e’i, G0, LS) и can_share(βr, ei + 1, e’i + 1, G0, LS), где αr, βr ∈ Rr;
ei, ei + 1 ∈ NS ∩ S0 и или истинен предикат can_share(ownr, ei, ei + 1, G0, LS), или истинен предикат can_share(ownr, ei + 1, ei, G0, LS).
Условия реализации информационного потока по времени
Слайд 20Метод предотвращения запрещенных информационных потоков по времени
Метод 1. Условие применения метода. Пусть
Метод предотвращения запрещенных информационных потоков по времени
Метод 1. Условие применения метода. Пусть

Шаг 1. Создать в системе доверенный субъект u ∈ LS ∩ S0, который будет реализовывать блокирующие доступы.
Шаг 2. Для каждого запрещенного информационного потока по времени (x, y, writet), где x и y ⎯ недоверенные субъекты, использовать алгоритм проверки истинности предиката can_write_time_block(x, y, G0, LS). Если предикат can_write_time_block(x, y, G0, LS) является истинным, рассмотреть все пути (пролеты моста) в G0, с использованием которых возможна реализация информационного потока. Если для всех запрещенных информационных потоков из Nf по времени предикат can_write_time_block(x, y, G0, LS) является ложным, то закончить применение метода.
Шаг 3. Для каждого пути, определенного на шаге 2, определить его вид. Возможны два вида путей. Если путь первого вида, то с его использованием реализуется информационный поток по памяти. Если путь второго вида, то с его использованием может быть реализован только информационный поток по времени.
Шаг 4. Если пролет моста первого вида, то удалить любое ребро пути (удалить у недоверенного субъекта право доступа к сущности). Перейти на шаг 2.
Шаг 5. Если путь второго вида реализовать блокирующий доступ доверенного субъекта u к любой сущности, не являющейся субъектом и принадлежащей пути. Перейти на шаг 2.
Теорема. Пусть G0 = (S0, E0, R0 ∪ A0 ∪ F0, H0) ⎯ начальное состояние системы Σ(G*, OP, G0). Пусть определены множества доверенных субъектов LS, недоверенных субъектов NS и запрещенных информационных потоков Nf. Тогда в результате применения в системе метода 1 для каждого информационного потока (x, y, writet) ∈ Nf, где x и y ⎯ недоверенные субъекты, предикат can_write_time_block(x, y, G0, LS) является ложным.
Слайд 21ДП-модель с функционально ассоциированными с субъектами сущностями
ДП-модель с функционально ассоциированными с субъектами сущностями
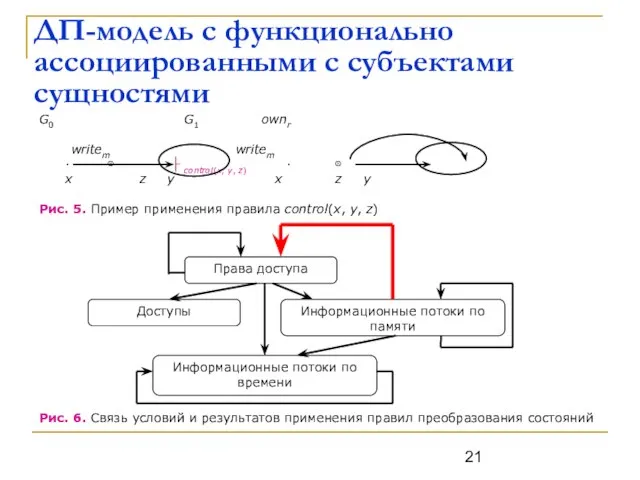
Слайд 22ДП-модель с функционально ассоциированными с субъектами сущностями
Определение. Доверенного субъекта y назовем функционально
ДП-модель с функционально ассоциированными с субъектами сущностями
Определение. Доверенного субъекта y назовем функционально

Определение. Доверенного субъекта y назовем корректным относительно сущности e, не являющейся доверенным субъектом, если субъект y не реализует информационный поток по памяти от сущности e к сущности e’, функционально ассоциированной с некоторым доверенным субъектом y’. При этом по определению каждый доверенный субъект корректен относительно другого доверенного субъекта.
Слайд 23ДП-модель для политики безопасного администрирования
Определение. В политике безопасного администрирования рассматриваются две угрозы
ДП-модель для политики безопасного администрирования
Определение. В политике безопасного администрирования рассматриваются две угрозы

Угроза 1. Наличие у пользователя возможности разместить ресурсы на компьютере (запустить процесс или разместить на компьютере файлы) несет угрозу получения им всех прав доступа и привилегий на данном компьютере.
Угроза 2. Обращение пользователя к компьютеру (с целью получить данные файлов локально или по сетевым коммуникационным каналам) несет угрозу захвата его прав доступа и привилегий пользователем, разместившим свои ресурсы на этом компьютере.
Предположение. Будем считать, что нарушитель имеет два уровня возможностей:
если нарушитель может разместить на компьютере свой ресурс, то он имеет возможность управления функциями КС (нарушитель третьего уровня);
если нарушитель может только удаленно обращаться к компьютеру, то он имеет возможность ведения диалога с КС (нарушитель первого уровня).
Определение. Будем говорить, что в КС реализована политика безопасного администрирования тогда, и только тогда, когда в КС выполняется следующее условие: получение нарушителем полного контроля (всех привилегий и прав доступа к сущностям, размещенным на компьютере) над компьютером КС не должно приводить к захвату нарушителем полного контроля над другими компьютерами КС посредством реализации нарушителем угроз 1 и 2.
Слайд 24ДП-модель для политики абсолютного разделения административных и пользовательских полномочий
Определение. Для системы Σ(G*,
ДП-модель для политики абсолютного разделения административных и пользовательских полномочий
Определение. Для системы Σ(G*,

G0 ⎯ начальное состояние для пользовательских траекторий функционирования системы P(G0), на которых недоверенные пользователи выполняют свои функции в системе;
GA0 ⎯ начальное состояние для административных траекторий функционирования системы P(GA0), предназначенных только для администрирования системы.
Предположение. На всех траекториях системы из множеств P(G0) и P(GA0) определены доверенные пользователи, обладающие правом доступа владения к каждой сущности, размещенной на компьютере. Кроме того, на траекториях системы из множества P(G0):
определен доверенный пользователь kernelc ∈ S ⎯ пользователь-«ядро ОС», при этом всегда выполняется условие (kernelc, ownr) ∈ RC(c);
всегда найдется недоверенный пользователь, активизировавший процесс от своего имени на компьютере c.
Предположение. Доверенный пользователь kernelc реализован функционально корректным и корректным относительно всех сущностей ECE(c) компьютера c. На траекториях P(GA0) активизируют процессы только доверенные пользователи, которые являются корректными относительно всех сущностей ECE(c) компьютера c. Если в системе Σ(G*, OP) существует доверенный пользователь s1 ∈ S \ {kernelc}, который в состоянии G = (S, E, R ∪ A ∪ F, H) системы активизировал процесс от своего имени на компьютере c ∈ EC, то выполняются условия (s1, c, writer) ∈ R, ECE(c) ⊂ [s1]. При этом, если недоверенный пользователь s2 ∈ S в состоянии G системы активизировал процесс от своего имени на компьютере c, то выполняется условие s2 ∈ [s1].
Слайд 25Методы предотвращения возможности получения права доступа владения
Метод предотвращения возможности получения права доступа
Методы предотвращения возможности получения права доступа владения
Метод предотвращения возможности получения права доступа

Метод реализации политики безопасного администрирования (для распределенных КС);
Метод реализации политики абсолютного разделения административных и пользовательских полномочий (для рабочих станций пользователей).
Слайд 26Мандатная ДП-модель. Виды запрещенных информационных потоков
Определение. Определим как запрещенные в КС с
Мандатная ДП-модель. Виды запрещенных информационных потоков
Определение. Определим как запрещенные в КС с

Информационные потоки по памяти и по времени между сущностями одного уровня конфиденциальности (определяются в соответствии с априорно заданной политикой управления доступом и информационными потоками).
Информационные потоки по памяти от сущностей с большим уровнем конфиденциальности к сущностям с меньшим уровнем конфиденциальности информации.
Информационные потоки по времени от сущностей с большим уровнем конфиденциальности к сущностям с меньшим уровнем конфиденциальности информации.
Информационные потоки по памяти от субъектов с низким уровнем доступа к субъектам с высоким уровнем доступа или к сущностям, функционально ассоциированным с субъектами с высоким уровнем доступа.
Слайд 27Мандатная ДП-модель.
Основные определения
(L, ≤) ⎯ решетка линейно упорядоченных уровней доступа и
Мандатная ДП-модель.
Основные определения
(L, ≤) ⎯ решетка линейно упорядоченных уровней доступа и

ES ⊂ E \ S ⎯ множество сущностей, которые могут быть применены для создания новых субъектов.
Определим функции:
fs: S → L ⎯ функция, определяющая уровень доступа каждого субъекта системы Σ(G*, OP);
fe: E \ S → L ⎯ функция, определяющая уровень конфиденциальности каждой сущности системы, не являющейся субъектом, при этом, если для двух сущностей e1, e2 ∈ E выполняется неравенство e1 ≤ e2 (сущность e1 содержится в контейнере e2), то по определению выполняется условие fe(e1) ≤ fe(e2);
CCR: E \ S → {true, false} ⎯ функция, определяющая способ доступа к сущностям, не являющимся субъектами, внутри контейнеров.
Определение. В состоянии G = (S, E, R ∪ A ∪ F, H, (fs, fe), CCR) системы Σ(G*, OP) доступ (s, e, α) ∈ A, где субъект s ∈ S, сущность e ∈ E \ S, вид доступа α ∈ Ra, обладает ss-свойством, если выполняются условия:
fs(s) ≥ fe(e);
для каждой сущности-контейнера e’ ∈ E \ S, такой, что e < e’ и CCR(e’) = true, выполняется неравенство fs(s) ≥ fe(e’).
Определение. В состоянии G = (S, E, R ∪ A ∪ F, H, (fs, fe), CCR) системы Σ(G*, OP) доступы (s, e1, reada), (s, e2, α) ∈ A, где субъект s ∈ S, сущности e1, e2 ∈ E \ S, вид доступа α ∈ {writea, appenda}, обладают *-свойством, если выполняется условие fe(e1) ≤ fe(e2).
Слайд 28Мандатная ДП-модель. Правила преобразования состояний
Мандатная ДП-модель. Правила преобразования состояний

Слайд 29Условия несанкционированного повышения уровня доступа субъекта
Теорема. Пусть уровень доступа l ∈ L
Условия несанкционированного повышения уровня доступа субъекта
Теорема. Пусть уровень доступа l ∈ L

Условие 1. Субъект y функционально некорректен относительно субъекта x.
Условие 2. Существует субъект y’ ∈ S0 такой, что fs0(y’) > l, и субъект y некорректен относительно сущности x и субъекта y’.
Условие 3. Существует сущность e ∈ E0 такая, что e ∈ [y], fe0(e) ≤ l, и для каждой сущности-контейнера e’ ∈ E0 такой, что e < e’ и CCR0(e’) = true, выполняется неравенство fe0(e’) ≤ l.
Условие 4. Существуют сущность e ∈ E0 и субъект y’ ∈ S0 такие, что fe0(e) ≤ l, fs0(y’) > l, и для каждой сущности-контейнера e’ ∈ E0 такой, что e < e’ и CCR0(e’) = true, выполняется неравенство fe0(e’) ≤ l, и субъект y некорректен относительно сущности e и субъекта y’.
Слайд 30Информационные потоки по времени
Информационные потоки по времени

Слайд 31Мандатные ДП-модели
Мандатная ДП-модель с блокирующими доступами доверенных субъектов;
ДП-модель с отождествлением порожденных субъектов
Мандатные ДП-модели
Мандатная ДП-модель с блокирующими доступами доверенных субъектов;
ДП-модель с отождествлением порожденных субъектов

ДП-модель для политики строгого мандатного управления доступом (в системе могут существовать несколько недоверенных субъектов, каждый из которых реализует доступы к сущностям только одного уровня конфиденциальности).
Слайд 32Метод предотвращения возможности реализации запрещенных информационных потоков по времени
Метод. Условие применения метода.
Метод предотвращения возможности реализации запрещенных информационных потоков по времени
Метод. Условие применения метода.

Шаг 1. Выделить в системе Σ(G*, OP, G0) компьютеры EC1, функциональность которых ограничена.
Шаг 2. Для компьютеров из EC1 обеспечить доверенность всех активизируемых на них субъектов. Реализовать систему управления доступом системы таким образом, чтобы обеспечивалась безопасность в смысле Белла-ЛаПадула доступов доверенных субъектов.
Шаг 3. Выделить компьютеры EC2, на каждом из которых должна быть обеспечена возможность активизации субъектов от имени только одного недоверенного субъекта-пользователя.
Шаг 4. Если это необходимо для реализации используемой в моделируемой реальной КС технологии обработки информации, то для каждого недоверенного субъекта-пользователя компьютера из EC2, во множество доступных ему сущностей включить сущности, размещенные на компьютерах из EC1. При этом реализовать иерархию подчиненности сущностей системы, обеспечивающую невозможность доступов недоверенных субъектов к сущностям в одной иерархии.
Шаг 5. Реализовать систему управления доступом системы Σ(G*, OP, G0) таким образом, чтобы обеспечивалась безопасность доступов доверенных субъектов компьютеров из EC2 в смысле Белла-ЛаПадула, доступов недоверенных субъектов, активизированных от имени субъектов-пользователей компьютеров из EC2, в смысле Белла-ЛаПадула с отождествлением порожденных субъектов.
Шаг 6. Выделить компьютеры EC3, на каждом из которых должна быть обеспечена возможность активизации субъектов несколькими недоверенными субъектами-пользователями. При этом реализовать иерархию подчиненности компьютеров системы, удовлетворяющую условию: для любых c1 ∈ EC2, c2 ∈ EC3 не выполняется одно из сравнений: c1 < c2 или c2 < c1.
Шаг 7. Если это необходимо для реализации используемой в моделируемой реальной КС технологии обработки информации, то для каждого недоверенного субъекта-пользователя user ∈ NS, активизирующего субъектов на компьютерах из EC3, во множество сущностей EU(user) включить сущности, размещенные на компьютерах из EC1. При этом реализовать иерархию подчиненности сущностей системы, обеспечивающую невозможность доступов недоверенных субъектов к сущностям в одной иерархии.
Шаг 8. Реализовать систему управления доступом системы Σ(G*, OP, G0) таким образом, чтобы обеспечивалась безопасность доступов доверенных субъектов компьютеров из EC3 в смысле Белла-ЛаПадула, недоверенных субъектов-пользователей компьютеров из EC3 в смысле строгого мандатного управления доступом.
Шаг 9. Реализовать всех доверенных субъектов системы Σ(G*, OP, G0) таким образом, чтобы на всех траекториях функционирования системы доверенные субъекты не создавали недоверенных субъектов.
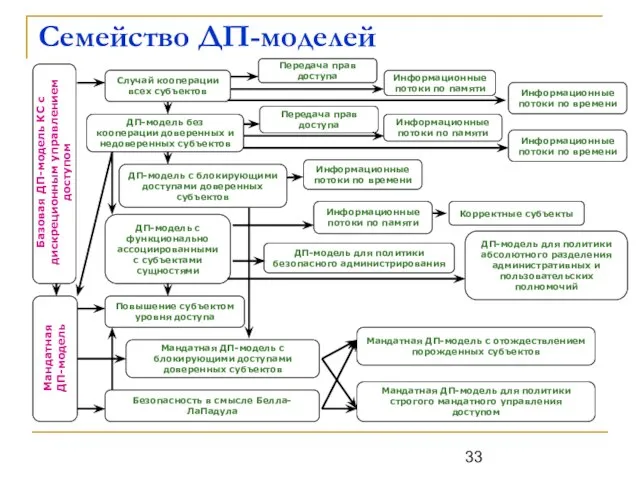
Слайд 33Семейство ДП-моделей
Семейство ДП-моделей
 Двигатель внутреннего сгорания
Двигатель внутреннего сгорания Химическая промышленность
Химическая промышленность Использование компьютерных технологий в начальной школе
Использование компьютерных технологий в начальной школе Производство корундовой броне-керамики в АО УАПО
Производство корундовой броне-керамики в АО УАПО Маршрут помощи детям с ограниченными возможностями
Маршрут помощи детям с ограниченными возможностями Бидермейер, бидермайер (нем. Biedermeier), стилевое направление в немецком и австрийском искусстве 1810–1840-х гг. Название получило позже,
Бидермейер, бидермайер (нем. Biedermeier), стилевое направление в немецком и австрийском искусстве 1810–1840-х гг. Название получило позже,  Презентация на тему Электрические явления
Презентация на тему Электрические явления  Александр Николаевич Островский. Колумб Замоскворечья
Александр Николаевич Островский. Колумб Замоскворечья Земля наш дом
Земля наш дом Презентация на тему 8 Марта
Презентация на тему 8 Марта  Маковельская Инна Николаевна
Маковельская Инна Николаевна Проекты ВПН
Проекты ВПН Рабелок Оптимальная Рабелок натрия 20мг форма выпуска Рабелок натрия 10мг
Рабелок Оптимальная Рабелок натрия 20мг форма выпуска Рабелок натрия 10мг Повторение сложения и вычитания в пределах 100 и таблицы умножения
Повторение сложения и вычитания в пределах 100 и таблицы умножения Конференция CyberMarketing 2011
Конференция CyberMarketing 2011 Russia at War 1941 1945
Russia at War 1941 1945 Воспитательная работа с детьми девиантного поведения и проблемными семьями
Воспитательная работа с детьми девиантного поведения и проблемными семьями Псалом 56. Святорусская редакция
Псалом 56. Святорусская редакция Презентацияурока по экономической и социальной географии мира
Презентацияурока по экономической и социальной географии мира СD DVD Blue Ray Flash как носители информации
СD DVD Blue Ray Flash как носители информации  Вязаные игрушки
Вязаные игрушки Государственная Дума РФ
Государственная Дума РФ Налогообложение на доходы иностранных лиц. Антиофшорное регулирование
Налогообложение на доходы иностранных лиц. Антиофшорное регулирование Акварель Составлено доцентом кафедры изобразительного искусства СыктГУ Торлоповой Натальей Геннадьевной 2006
Акварель Составлено доцентом кафедры изобразительного искусства СыктГУ Торлоповой Натальей Геннадьевной 2006 Политика и власть
Политика и власть Права и обязанности граждан
Права и обязанности граждан Сообщение по биологии на тему «Утконос» Ученика 7В класса школы №5 Бережняка Никиты
Сообщение по биологии на тему «Утконос» Ученика 7В класса школы №5 Бережняка Никиты Воспитание культурно-гигиенических навыков у детей средней группы детского сада
Воспитание культурно-гигиенических навыков у детей средней группы детского сада