Анализ расчета осадок зданий и сооружений по методам актуализированных редакций СНиП 2.02.01-83*(СП 22.13330.2011) «Основания зданий и соору

В СП 50-101-2004 и СП 22.13330.2011 для расчета осадок фундамента нужно определить глубину сжимаемой толщи основания Нс, которая принимается постоянной (???) по всей площади фундамента. Но условие σz=kγz дает существенно различные Нс под различными точками фундамента.
Если все же принять Нс=сonst, то в какой точке? Для прямоугольных в плане фундаментов эта точка - геометрический центр. Для кольцевого фундамента такой центр лежит вне фундамента. Для фундаментов более сложных форм в плане, а таких становится все больше, вопрос о выборе Нс в СП 50-101-2004 и СП 22.13330.2011 не рассматривается.
А как быть с Нс для разновысоких зданий на одной общей плите?
В СП 22.13330.2011 для разных категорий сооружений введены две разных модели: сжимаемая толща линейно-деформируемого полупространства (СТЛДП), а для предварительных расчетов неответственных сооружений – линейно-деформируемый слой (ЛДС). Между тем, расчеты с использованием этих моделей одинаково трудоемки. А ЛДС более достоверна в случае залегания скалы на небольшой глубине, но этот случай не рассмотрен.

тс – коэффициент, учитывающий размеры фундамента и принимаемый равным 1 для сооружений, имеющих ширину менее 20 м или площадь менее 500 м2; в других случаях коэффициент тс определяется по формуле
Сейчас в СП 2010 принято k=0.5 при любой ширине фундамента, т.е.
как в CНиП 2.02.02-85. «Основания гидротехнических сооружений»,
Но в CНиП 2.02.02-85– модуль деформации меняется скачком
Расчет осадок для однородного основания выполняется с использованием осредненного по глубине модуля деформации

Неверен термин "линейно-”деформируемый слой (ЛДС) «линейно-” деформируемое» полупространство (ЛДП), т.к. осадки основания зависят от прилагаемой нагрузки нелинейно.
Пример
р– равномерная нагрузка на основание; γ – объемный вес грунта; k=0.5
где Е0 – модуль деформации основания.
Учет образования зон разрушения грунта под краями фундамента
увеличивает нелинейность осадок
Критерий «расчетное сопротивление грунта основания» давно устарел.
Осадка зависит от нагрузки по квадратичному, т.е. нелинейному закону
(1)
Нелинейность
(2)
Сжимаемая толща в одномерной задаче

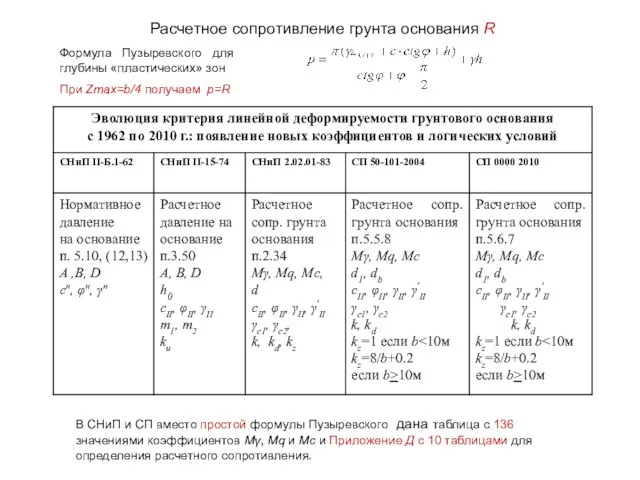
Расчетное сопротивление грунта основания R
Формула Пузыревского для глубины «пластических» зон
При Zmax=b/4 получаем p=R
В СНиП и СП вместо простой формулы Пузыревского дана таблица с 136 значениями коэффициентов Мγ, Мq и Мс и Приложение Д с 10 таблицами для определения расчетного сопротивления.

При использовании "ЛДС" и "СТЛДП" не учитывается образование зон разрушения грунта (прорезка) под краями фундамента. В строгих решениях контактные давления, под краями фундамента бесконечны, что затрудняет использование численных методов, приводит к искажению результатов расчета усилий в фундаментах, прогибов, кренов и осадок.
Благодаря прорезке контактные давления под краями фундамента конечны, Прорезка дает свой вклад в нелинейность зависимости «нагрузка-осадка» особенно для оснований, сложенных слабыми грунтами
Прорезка – простейший способ учета образования зон разрушения под краями фундамента

Михеев, Серебряный, Смородинов ОФМГ 1961
Семинар PLAXIS CПб 2007

«Прорезка» грунта под краями штампа
ОФМГ 2007, ceминар PLAXIS CПб 2007
Болдырев и Никитин ОФМГ 1987

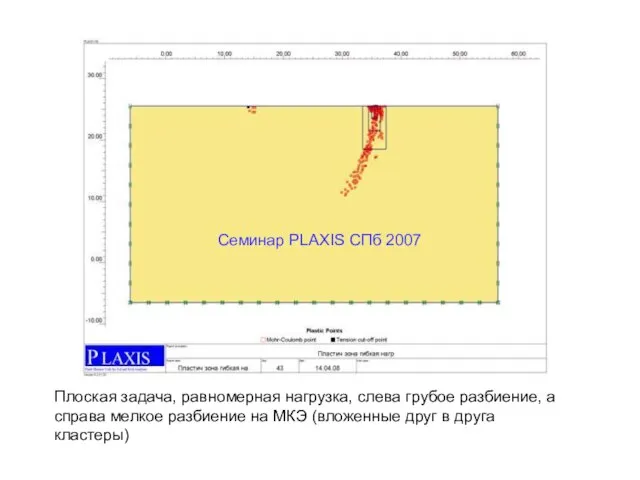
Семинар PLAXIS CПб 2007
Плоская задача, равномерная нагрузка, слева грубое разбиение, а справа мелкое разбиение на МКЭ (вложенные друг в друга кластеры)

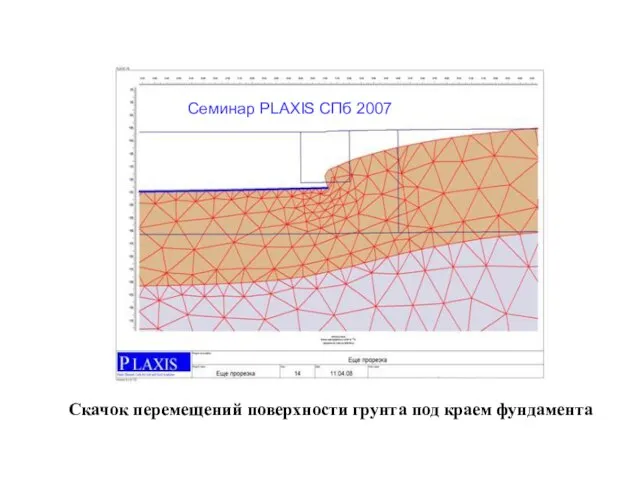
Скачок перемещений поверхности грунта под краем фундамента
Семинар PLAXIS CПб 2007

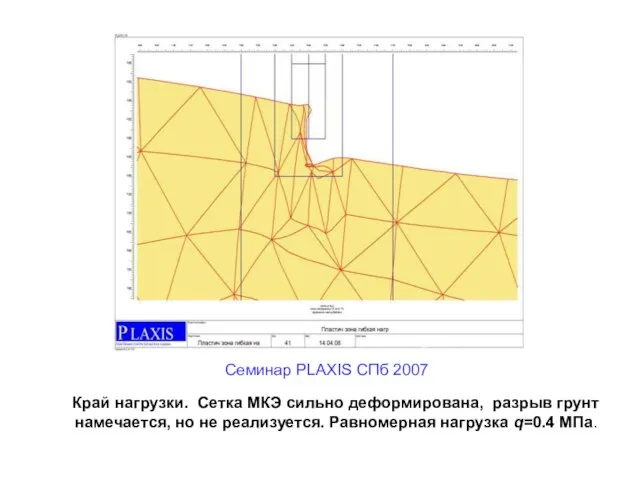
Край нагрузки. Сетка МКЭ сильно деформирована, разрыв грунт намечается, но не реализуется. Равномерная нагрузка q=0.4 МПа.
Семинар PLAXIS CПб 2007

Семинар PLAXIS CПб 2007
Распределение контактных давлений
под штампом в осесимметричной задаче

Расчет 11. 2D. Жесткий фундамент шириной 30 м, q=5 кПа, Грунт: Е=30 МПа, c=5 кПа, φ=33o. Даже при малой нагрузке возникают пластические зоны, форма которых зависит
от измельчения сетки
Семинар PLAXIS CПб 2007

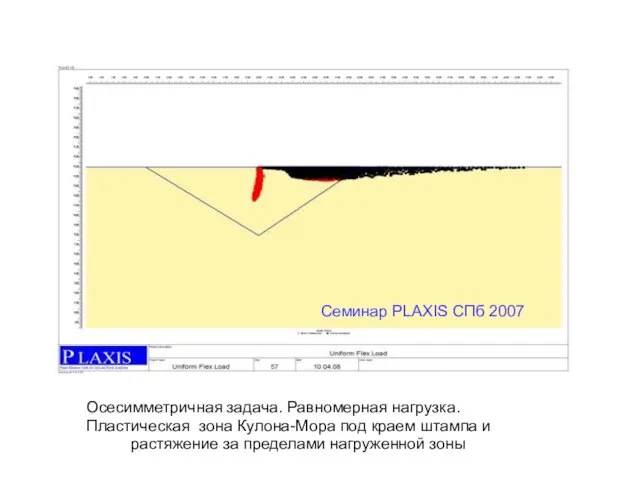
Семинар PLAXIS CПб 2007
Осесимметричная задача. Равномерная нагрузка.
Пластическая зона Кулона-Мора под краем штампа и
растяжение за пределами нагруженной зоны

Fi=38o c=0.2 тс/м2 R0=222.5 тс/м2
PLAXIS. Пластические зоны от равномерной нагрузки, равной R - расчетному сопротивлению грунта основания

Fi=36o c=0.4 тс/м2 R0=194,6 тс/м2
PLAXIS. Пластические зоны от равномерной нагрузки, равной расчетному сопротивлению грунта основания

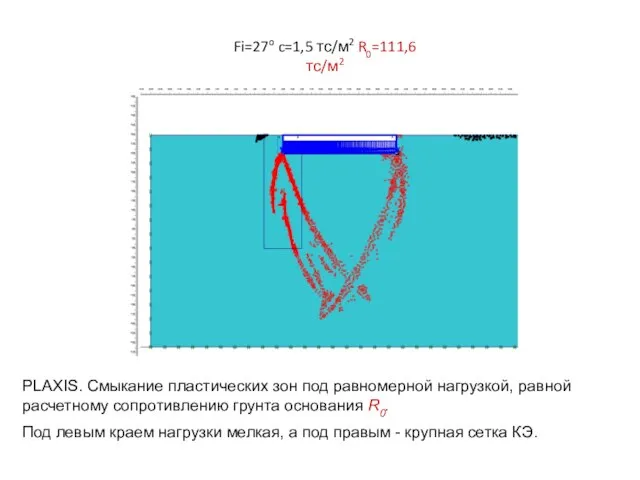
Fi=27o c=1,5 тс/м2 R0=111,6 тс/м2
PLAXIS. Смыкание пластических зон под равномерной нагрузкой, равной расчетному сопротивлению грунта основания R0.
Под левым краем нагрузки мелкая, а под правым - крупная сетка КЭ.

Fi=24o c=1,3 тс/м2 R0=90.1 тс/м2
PLAXIS. Пластические зоны от равномерной нагрузки, равной расчетному сопротивлению грунта основания. Под левым краем фундамента мелкая сетка КЭ

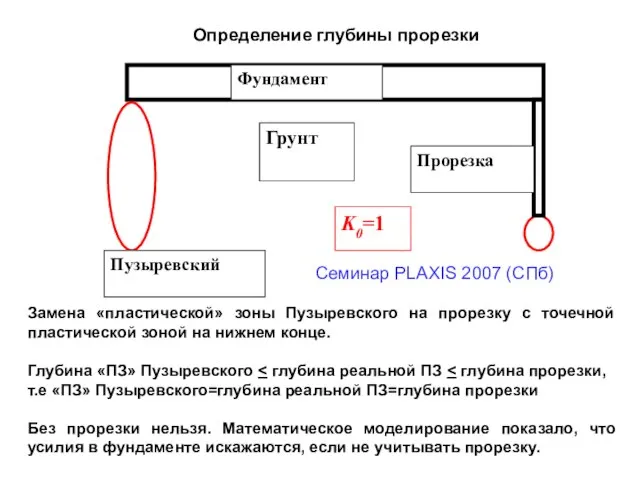
Замена «пластической» зоны Пузыревского на прорезку с точечной пластической зоной на нижнем конце.
Глубина «ПЗ» Пузыревского < глубина реальной ПЗ < глубина прорезки,
т.е «ПЗ» Пузыревского=глубина реальной ПЗ=глубина прорезки
Без прорезки нельзя. Математическое моделирование показало, что усилия в фундаменте искажаются, если не учитывать прорезку.
Семинар PLAXIS 2007 (CПб)
Определение глубины прорезки

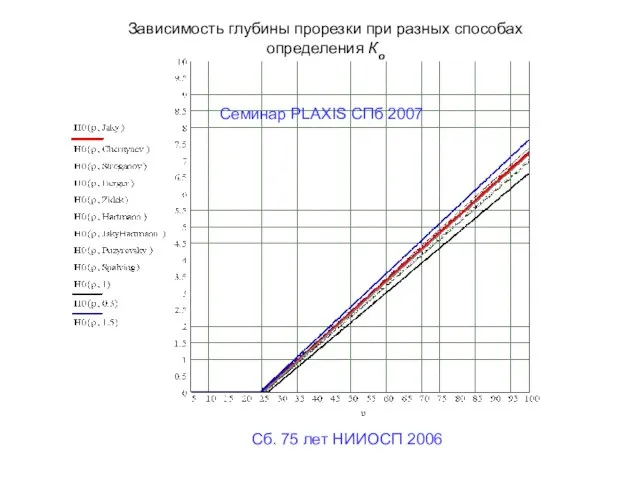
Сб. 75 лет НИИОСП 2006
Семинар PLAXIS CПб 2007
Зависимость глубины прорезки при разных способах определения Ко

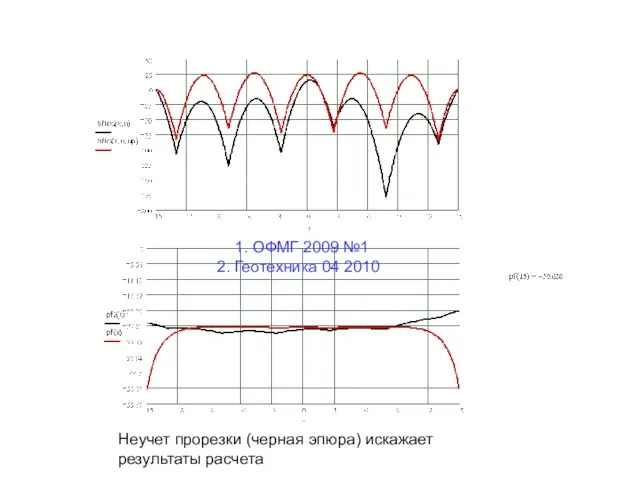
1. ОФМГ 2009 №1
2. Геотехника 04 2010
Неучет прорезки (черная эпюра) искажает результаты расчета

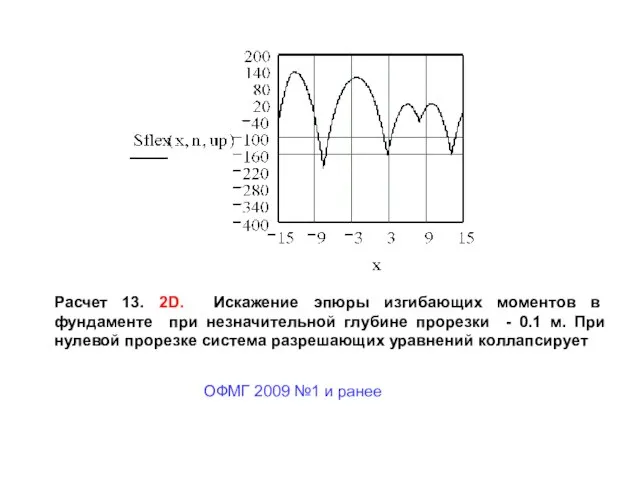
Расчет 13. 2D. Искажение эпюры изгибающих моментов в фундаменте при незначительной глубине прорезки - 0.1 м. При нулевой прорезке система разрешающих уравнений коллапсирует
ОФМГ 2009 №1 и ранее

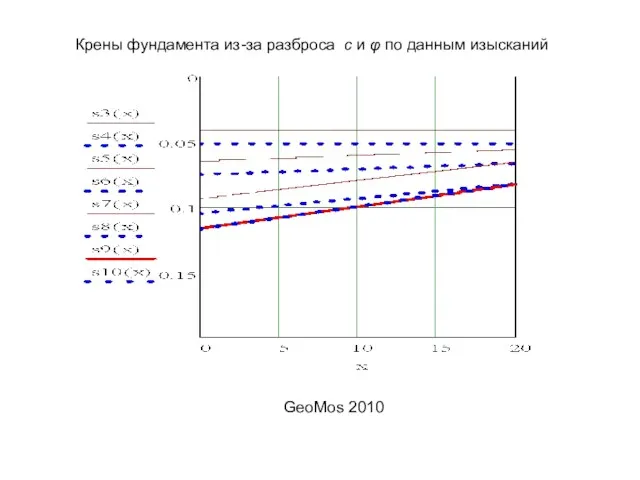
При различных значениях с и φ под краями фундамента возникают крены. Здесь различия с и φ были взяты по разбросу из инж-геол отчета
GeoMos 2010

Крены фундамента из-за разброса с и φ по данным изысканий
GeoMos 2010

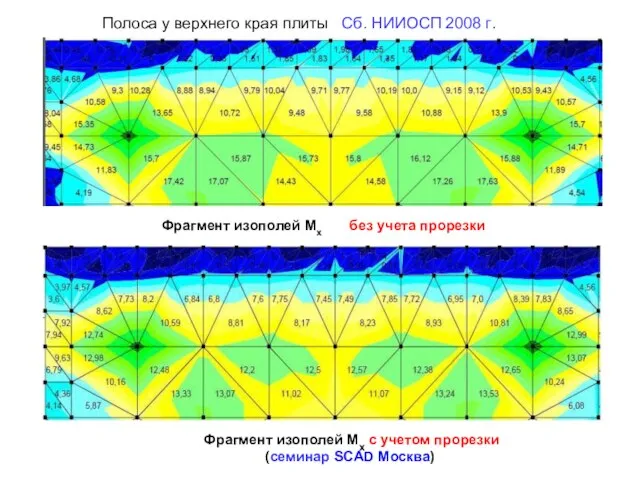
Фрагмент изополей Мх без учета прорезки
Фрагмент изополей Мх с учетом прорезки (семинар SCAD Москва)
Полоса у верхнего края плиты Сб. НИИОСП 2008 г.

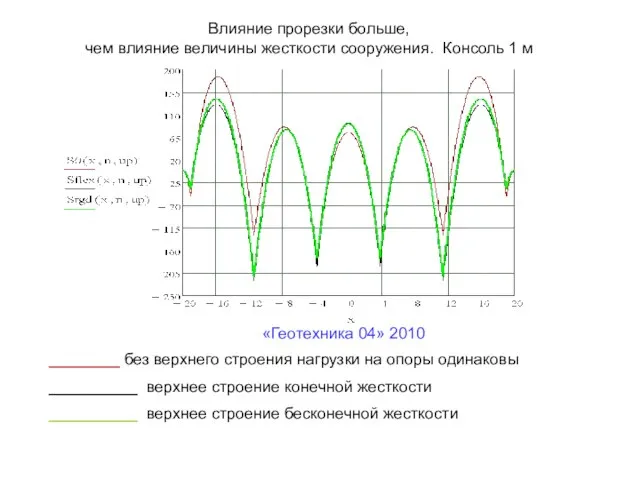
«Геотехника 04» 2010
Влияние прорезки больше,
чем влияние величины жесткости сооружения. Консоль 1 м
________ без верхнего строения нагрузки на опоры одинаковы
__________ верхнее строение конечной жесткости
__________ верхнее строение бесконечной жесткости

Предлагается заменить
модель «сжимаемой толщи линейно-деформируемого полупространства»
на полупространство с модулем деформации E(z)=Eo(1+Az)2
где A=γ/(3p) из условий одномерной задачи
Если СТЛДП достоверна (откалибрована по данным мониторинга осадок),
то достоверна и эта модель, т.к. они дают очень близкие значения осадок
Тогда формула послойного интегрирования будет выглядеть так:
S=(1-ν2)S0 , где
h – заглубление фундамента, Но – глубина прорезки, n=E/Ee
∞ заменяется на большую величину, например на 4b

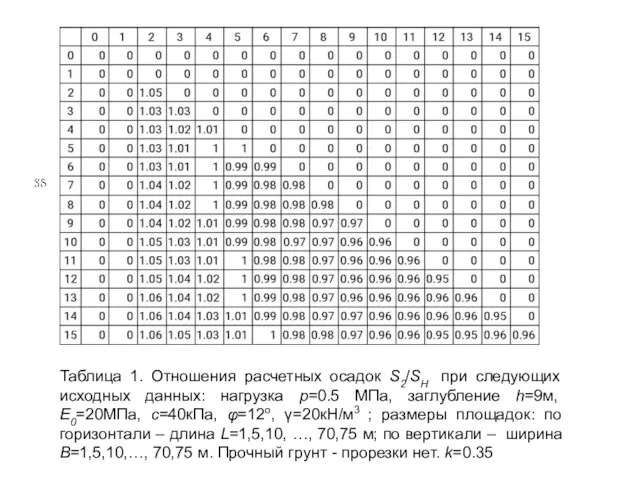
Таблица 1. Отношения расчетных осадок S2/SН при следующих исходных данных: нагрузка р=0.5 МПа, заглубление h=9м, Е0=20МПа, с=40кПа, φ=12о, γ=20кН/м3 ; размеры площадок: по горизонтали – длина L=1,5,10, …, 70,75 м; по вертикали – ширина В=1,5,10,…, 70,75 м. Прочный грунт - прорезки нет. k=0.35

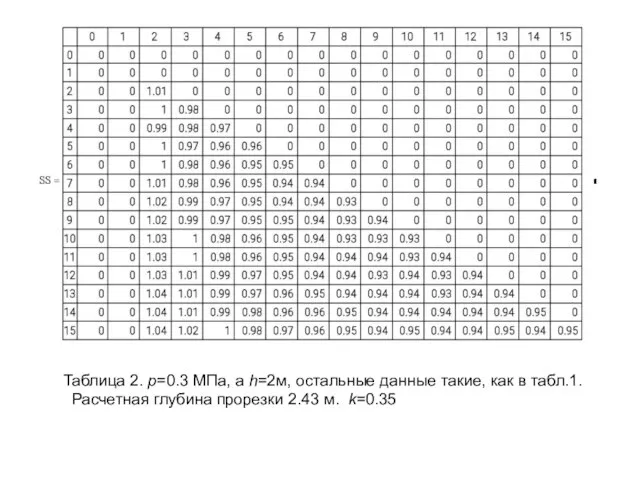
Таблица 2. р=0.3 МПа, а h=2м, остальные данные такие, как в табл.1.
Расчетная глубина прорезки 2.43 м. k=0.35

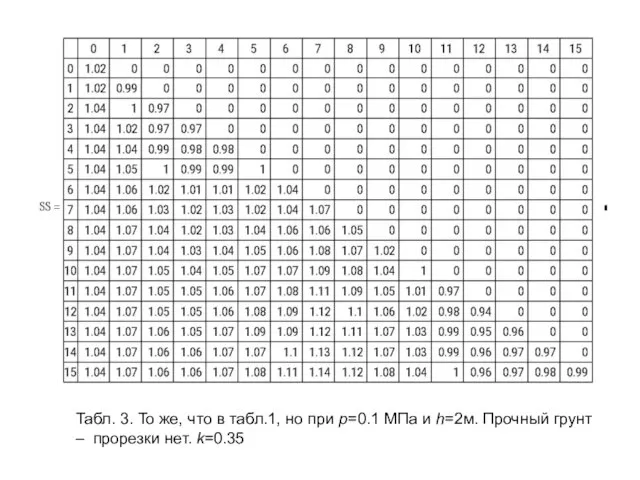
Табл. 3. То же, что в табл.1, но при р=0.1 МПа и h=2м. Прочный грунт – прорезки нет. k=0.35

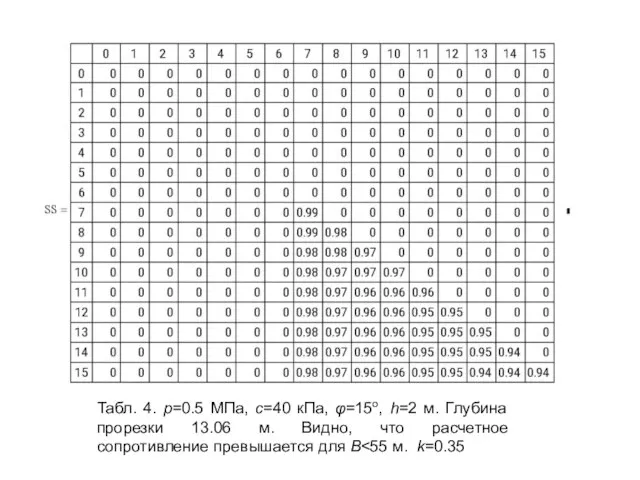
Табл. 4. р=0.5 МПа, c=40 кПа, φ=15о, h=2 м. Глубина прорезки 13.06 м. Видно, что расчетное сопротивление превышается для B<55 м. k=0.35

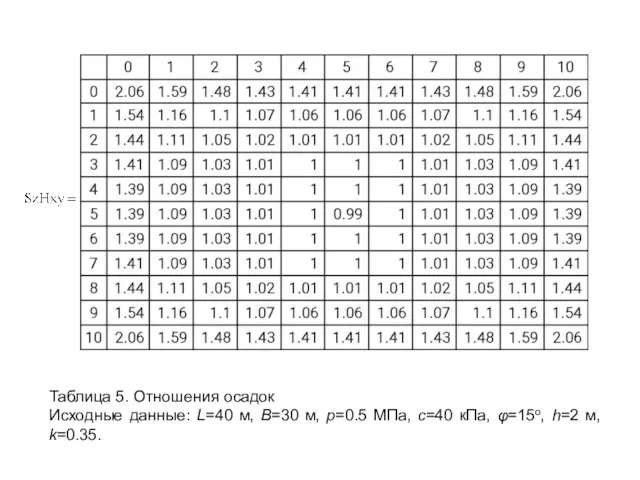
Таблица 5. Отношения осадок
Исходные данные: L=40 м, B=30 м, р=0.5 МПа, c=40 кПа, φ=15о, h=2 м, k=0.35.

Установившийся УПВ при нейтральном поровом давлении в грунте не влияет на глубину сжимаемой толщи и на осадки фундаментов.
Изменения УПВ – это крупномасштабное явление, которое влияет на большую территорию, увеличивая осадки всех фундаментов на этой территории на одну и ту же величину
Выталкивающие архимедовы силы, вызывают разгрузку основания, но соответствующие деформации незначительны, т.к. модуль деформации при разгрузке имеет большую величину.
Колебания УПВ могут изменить свойства грунтов, но сжимаемая толща здесь не при чем.
Напорные воды ниже слоя водоупора могут воспринимать всю внешнюю нагрузку (тогда фундамент всплывает) или ее часть (тогда из внешней нагрузки нужно вычесть поровое давление). Способ определения СТ в этом случае не
Уровень подземных вод (УПВ)