Анатомия составных частей компилятора

ТЕРМИНОЛОГИЯ
Транслятор - это программа, которая переводит исходную программу в эквивалентную ей объектную программу. Если объектный язык представляет собой автокод или некоторый машинный язык, то транслятор называется компилятором.
Автокод очень близок к машинному языку; большинство команд автокода - точное символическое представление команд машины.
Ассемблер - это программа, которая переводит исходную программу, написанную на автокоде или на языке ассемблера (что, суть, одно и то же), в объектный (исполняемый) код.
Интерпретатор принимает исходную программу как входную информацию и выполняет ее. Интерпретатор не порождает объектный код. Обычно интерпретатор сначала анализирует исходную программу (как компилятор) и транслирует ее в некоторое внутреннее представление. Далее интерпретируется (выполняется) это внутреннее представление.

Препроцессор
Препроцессор — это компьютерная программа — это компьютерная программа, принимающая данные на входе и выдающая данные, предназначенные для входа другой программы (например, компилятора). О данных на выходе препроцессора говорят, что они находятся в препроцессированной форме, пригодной для обработки последующими программами (компилятор). Результат и вид обработки зависят от вида препроцессора; так, некоторые препроцессоры могут только выполнить простую текстовую подстановку, другие способны по возможностям сравниться с языками программирования. Наиболее частый случай использования препроцессора — обработка исходного кода форме, пригодной для обработки последующими программами (компилятор). Результат и вид обработки зависят от вида препроцессора; так, некоторые препроцессоры могут только выполнить простую текстовую подстановку, другие способны по возможностям сравниться с языками программирования. Наиболее частый случай использования препроцессора — обработка исходного кода перед передачей его на следующий шаг компиляции. Языки программирования форме, пригодной для обработки последующими программами (компилятор). Результат и вид обработки зависят от вида препроцессора; так, некоторые препроцессоры могут только выполнить простую текстовую подстановку, другие способны по возможностям сравниться с языками программирования. Наиболее частый случай использования препроцессора — обработка исходного кода перед передачей его на следующий шаг компиляции. Языки программирования C форме, пригодной для обработки последующими программами (компилятор). Результат и вид обработки зависят от вида препроцессора; так, некоторые препроцессоры могут только выполнить простую текстовую подстановку, другие способны по возможностям сравниться с языками программирования. Наиболее частый случай использования препроцессора — обработка исходного кода перед передачей его на следующий шаг компиляции. Языки программирования C/C++ форме, пригодной для обработки последующими программами (компилятор). Результат и вид обработки зависят от вида препроцессора; так, некоторые препроцессоры могут только выполнить простую текстовую подстановку, другие способны по возможностям сравниться с языками программирования. Наиболее частый случай использования препроцессора — обработка исходного кода перед передачей его на следующий шаг компиляции. Языки программирования C/C++ и система компьютерной форме, пригодной для обработки последующими программами (компилятор). Результат и вид обработки зависят от вида препроцессора; так, некоторые препроцессоры могут только выполнить простую текстовую подстановку, другие способны по возможностям сравниться с языками программирования. Наиболее частый случай использования препроцессора — обработка исходного кода перед передачей его на следующий шаг компиляции. Языки программирования C/C++ и система компьютерной вёрстки форме, пригодной для обработки последующими программами (компилятор). Результат и вид обработки зависят от вида препроцессора; так, некоторые препроцессоры могут только выполнить простую текстовую подстановку, другие способны по возможностям сравниться с языками программирования. Наиболее частый случай использования препроцессора — обработка исходного кода перед передачей его на следующий шаг компиляции. Языки программирования C/C++ и система компьютерной вёрстки TeX используют препроцессоры, значительно расширяющие их возможности.

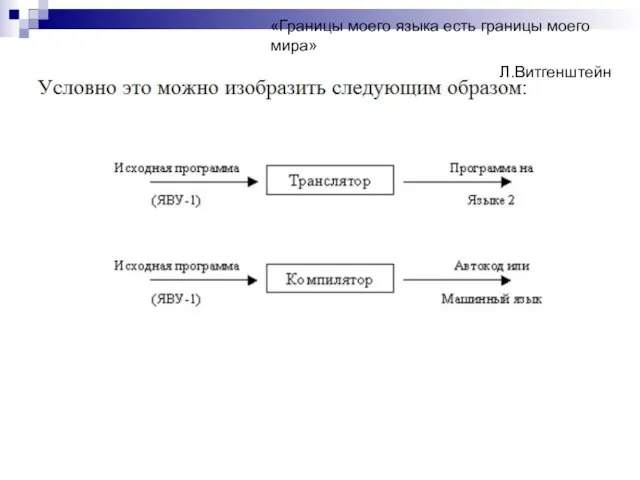
«Границы моего языка есть границы моего мира»
Л.Витгенштейн

Компилятор компиляторов
Компилятор компиляторов (КК) – система, позволяющая генерировать компиляторы; на входе системы - множество грамматик, а на выходе, в идеальном случае, - программа. Иногда под КК понимают язык программирования, в котором исходная программа - это описание компилятора некоторого языка, а объектная программа - сам компилятор для этого языка. Исходная программа КК - это просто формализм, служащий для описания компиляторов, содержащий, явно или неявно, описание лексического и синтаксического анализаторов, генератора кодов и других частей создаваемого компилятора.

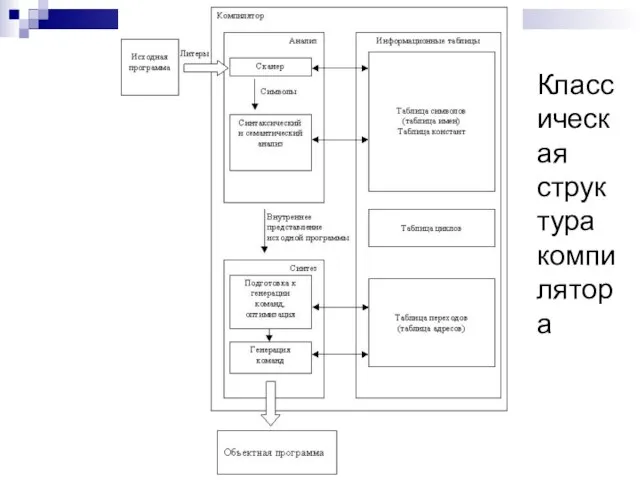
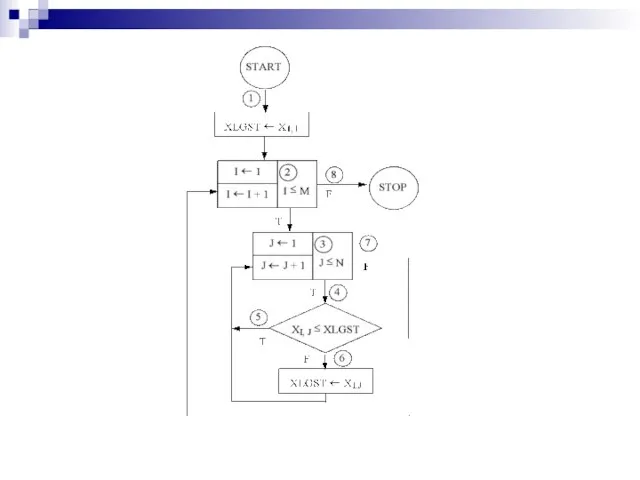
Классическая структура компилятора

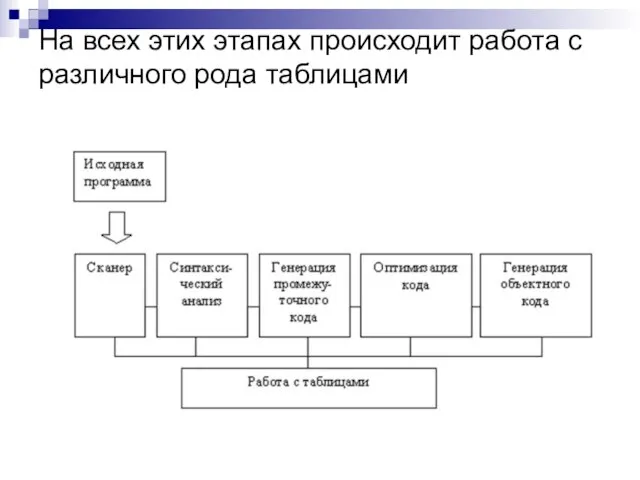
На всех этих этапах происходит работа с различного рода таблицами

Синтаксис. Семантика. Синтаксический анализатор.
Синтаксис - совокупность правил некоторого языка, определяющих формирование его элементов. Иначе говоря, это совокупность правил образования семантически значимых последовательностей символов в данном языке.
Семантика - правила и условия, определяющие соотношения между элементами языка и их смысловыми значениями, а также интерпретацию содержательного значения синтаксических конструкций языка.
Синтаксический анализатор - компонента компилятора, осуществляющая проверку исходных операторов на соответствие синтаксическим правилам и семантике данного языка программирования.

Лексический анализ (сканер)
На входе сканера - цепочка символов некоторого алфавита (именно так выглядит для сканера наша исходная программа). При этом некоторые комбинации символов рассматриваются сканером как единые объекты. Лексический анализатор (ЛА) группирует определенные терминальные символы (т.е. входные символы) в единые синтаксические объекты - лексемы. В простейшем случае лексема - это пара вида <тип_лексемы, значение>.

Как будет интерпретироваться такая входная последовательность "567АВ" ?

Прямой ЛА и непрямой ЛА
Прямой ЛА определяет лексему, расположенную непосредственно справа от текущего указателя, и сдвигает указатель вправо от части текста, образующей лексему (ПЛА определяет тип лексемы, которая образована символами справа от указателя).
Непрямой ЛА определяет, образуют ли знаки, расположенные непосредственно справа от указателя, лексему этого типа. Если да, то указатель передвигается вправо от части текста, образующей лексему. Иными словами, для него заранее задается тип лексемы, и он распознает символы справа от указателя и проверяет, удовлетворяют ли они заданному типу.

DO5I=1,10
Фортран – это классический пример языка, использующего непрямой лексический анализатор. Все дело в том, что в этом языке игнорируются пробелы. Рассмотрим, например, конструкцию
DO5I=1,10 …

Итак, на выходе сканера - внутреннее представление имен, разделителей и т.п.

Работа с таблицами
Таблица имен представляет собой структуру, подобную следующей:
Механизм работы с таблицами должен обеспечивать:
быстрое добавление новых идентификаторов и сведений о них;
быстрый поиск информации.

Синтаксический и семантический анализ
Синтаксический анализ - это процесс, в котором исследуется цепочка лексем и устанавливается, удовлетворяет ли она структурным условиям, явно сформулированным в определении синтаксиса языка. Это – самая сложная часть компилятора

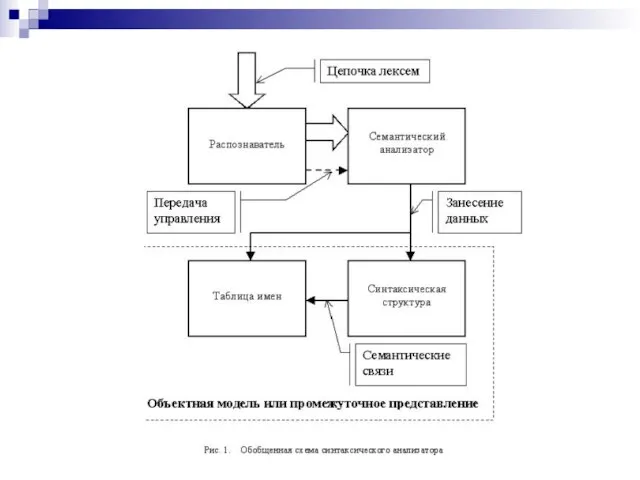
Синтаксический анализатор расчленяет исходную программу на составные части, формирует ее внутреннее представление, заносит информацию в таблицу символов и другие таблицы. При этом производится полный синтаксический и, по возможности, семантический контроль программы. Фактически, это - синтаксически управляемая программа. При этом обычно стремятся отделить синтаксис от семантики насколько это возможно - когда синтаксический анализатор распознает конструкцию исходного языка, он вызывает семантическую процедуру, которая контролирует эту конструкцию, заносит информацию куда надо, проверяет на дублирование описания переменных, проверяет соответствие типов и т.п.

Синтаксический анализатор можно разбить на следующие составляющие :
∙ распознаватель;
блок семантического анализа;
объектную модель, или промежуточное представление, состоящие из таблицы имен и синтаксической структуры.

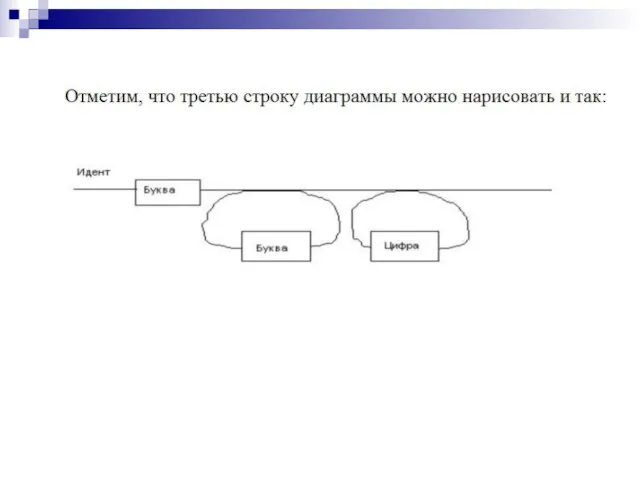
Предложения исходной программы обычно записываются в инфиксной форме

Три вида записи выражений
Существуют три вида записи выражений:
1. инфиксная форма, в которой оператор расположен между операндами (например, "а + b");
2. постфиксная форма, в которой оператор расположен после операндов ("а b + ");
3. префиксная форма, в которой оператор расположен перед операндами ("+ а b").
Постфиксная и префиксная формы образуют т.н. польскую форму записи (польская нотация). Польская форма удобна, прежде всего, тем, что в ней отсутствуют скобки.
в честь польского математика Лукасевича

Обычно под польской формой понимают именно постфиксную форму записи. Кроме того, используются и такие внутренние формы представления исходной программы, как дерево (синтаксическое) и тетрады.

Дерево.
Допустим, имеется входная цепочка i=(a+b)*c. Тогда дерево будет выглядеть так:
У каждого элемента дерева может быть только один “предок”. Дерево “читается” снизу вверх и слева направо. Дерево – это прежде всего удобная математическая абстракция.

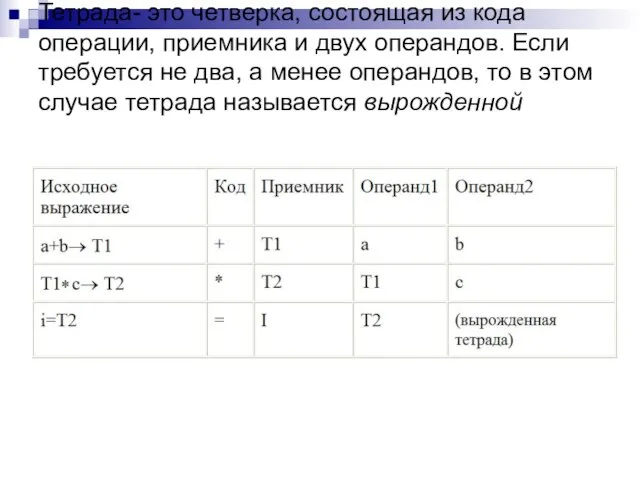
Тетрада- это четверка, состоящая из кода операции, приемника и двух операндов. Если требуется не два, а менее операндов, то в этом случае тетрада называется вырожденной

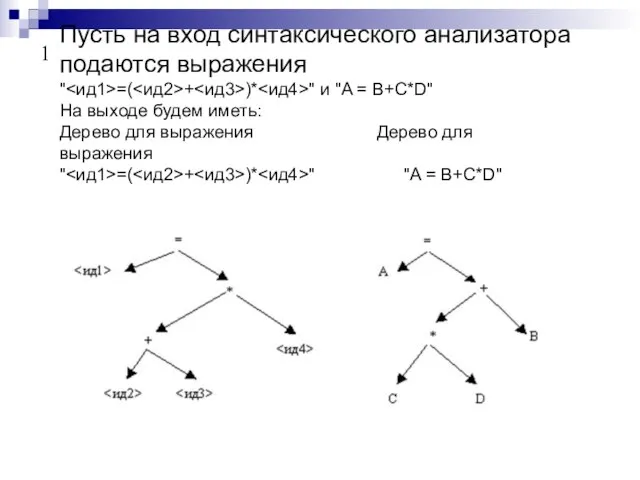
Пусть на вход синтаксического анализатора подаются выражения
"<ид1>=(<ид2>+<ид3>)*<ид4>" и "A = B+C*D"
На выходе будем иметь:
Дерево для выражения Дерево для выражения
"<ид1>=(<ид2>+<ид3>)*<ид4>" "A = B+C*D"
1

Тетрады для
"<ид1> = (<ид2>+<ид3>)*<ид4>"
+, <ид2>, <ид3>, T1
*, T1, <ид4>, T2
=, T2, <ид1>
Тетрады для "A = B+C*D"
*, C, D, T1
+, B, T1, T2
=, T2, A
(T1, T2 - временные переменные, созданные компилятором)
2

3
Польская форма для "<ид1> = (<ид2>+<ид3>)*<ид4>":
<ид1> <ид2> <ид3> + <ид4> * =
И еще один пример: польская форма для "A=B+C*D" будет выглядеть как "ABCD*+=".

Алгоритм вычисления польской формы записи очень прост:
Просматриваем последовательно символы входной цепочки. Если очередной символ является операндом (идентификатором или константой), то читаем дальше. Если символ является бинарным оператором, то извлекаем из цепочки два предыдущих операнда вместе с оператором, производим операцию и помещаем результат обратно в цепочку символов.
"ABCD*+=".

ТЕОРИЯ ФОРМАЛЬНЫХ ЯЗЫКОВ ГРАММАТИКИ
ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ
Общение на каком-либо языке – искусственном или естественном- заключается в обмене предложениями или, точнее, фразами. Фраза - это конечная последовательность слов языка. Фразы необходимо уметь строить и распознавать.
Если существует механизм построения фраз и механизм признания их корректности и понимания (механизм распознавания), то мы говорим о существовании некоторой теории рассматриваемого языка.

Определение: Язык L - это множество цепочек конечной длины в алфавите Σ .
Одним из наиболее эффективных способов описания языка является грамматика. Строго говоря, грамматика - это математическая система, определяющая язык. Грамматика пригодна не только для задания (или генерации) языка, но и для его распознавания.

Если ∑ - множество (алфавит или словарь), то ∑ * - замыкание множества ∑ , или, иначе, свободный моноид, порожденный ∑ , т.е. множество всех конечных последовательностей, составленных из элементов множества ∑ , включая и пустую последовательность.

Определение. Грамматика - это четверка G = (N, Σ ,P,S),
где
N - конечное множество нетерминальных символов (синтаксические переменные или синтаксические категории);
Σ - конечное множество терминальных символов (слов) (Σ ∩ N=∅ );
P - конечное подмножество множества
(N∪ Σ )*N(N∪ Σ )* × (N∪ Σ )*
Элемент (α ,β ) множества P называется правилом или продукцией и записывается в виде α → β ;
S - выделенный символ из N (S∈ N), называемый начальным символом (эта особая переменная называется также "начальной переменной" или "исходным символом").
http://www.masters.donntu.edu.ua/2006/fvti/svyezhentsev/library/article3.htm
http://www.chernyshov.com/SPPO_5/TRANS/Tr3-02.htm

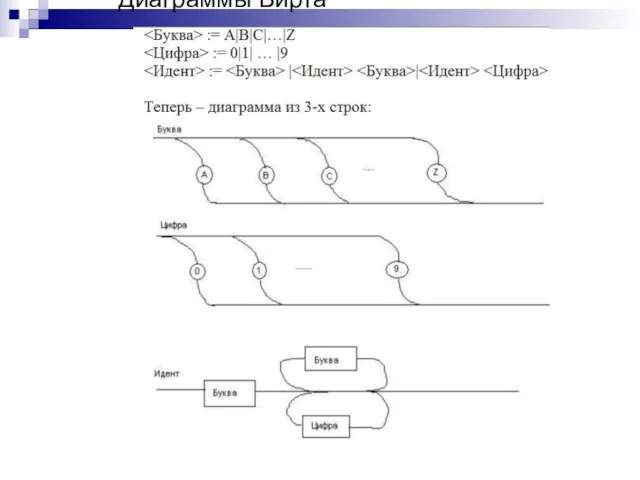
Нормальная форма Бэкуса-Наура
<Буква> := A|B|C|…|Z
<Цифра> := 0|1| … |9
<Идент> := <Буква> {<Буква>|<Цифра>}
Грамматика целых чисел без знака:
<число> := <цифра>|<цифра><число>
<цифра> := 0|1|2|…|9

Формула с плюсами и минусами без скобок
<формула> := <число>|<формула><знак><число>
<знак> := +|-

Диаграммы Вирта

ИЕРАРХИЯ ХОМСКОГО
Иерархия Хомского — классификация формальных языков — классификация формальных языков и формальных грамматик — классификация формальных языков и формальных грамматик, согласно которой они делятся на 4 типа по их условной сложности. Предложена профессором Массачусетского технологического института, лингвистом Ноамом Хомским.
Тип 0 — неограниченные
Тип 1 — контекстно-зависимые
Тип 2 — контекстно-свободные
Тип 3 — регулярные

Конечные автоматы

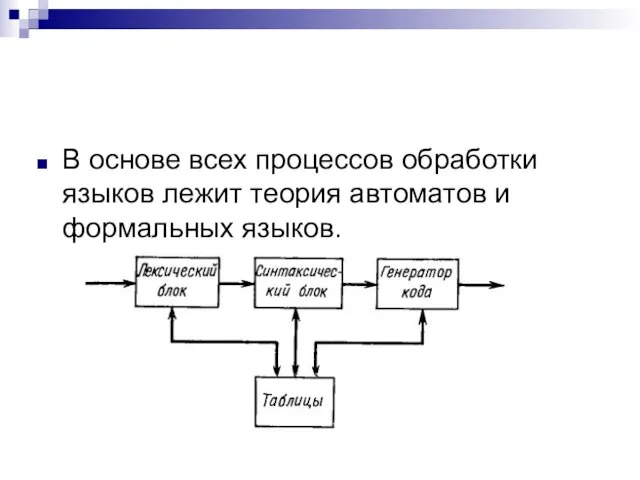
В основе всех процессов обработки языков лежит теория автоматов и формальных языков.

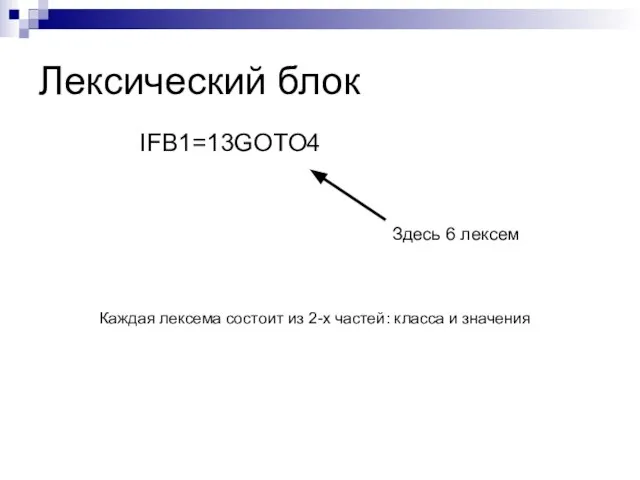
Лексический блок
IFB1=13GOTO4
Здесь 6 лексем
Каждая лексема состоит из 2-х частей: класса и значения

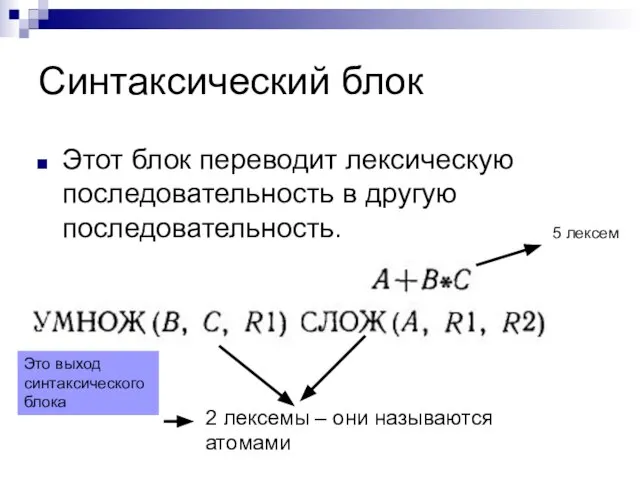
Синтаксический блок
Этот блок переводит лексическую последовательность в другую последовательность.
5 лексем
2 лексемы – они называются атомами
Это выход синтаксического блока

Генератор кода

Семантическая обработка

Оптимизация

Блоки и проходы компилятора

Конечные автоматы

Конечные распознаватели

Контроль нечетности

Входной алфавит

Переходы

Функция переходов

Конечный автомат

1101

Регулярные множества

Таблица переходов

Таким образом таблица переходов создаёт конечный автомат:

Ещё один автомат

Концевые маркеры и выходы из распознавания

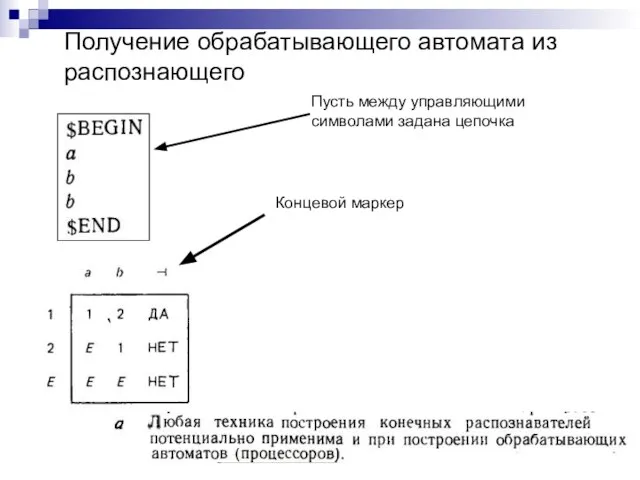
Пусть между управляющими символами задана цепочка
Концевой маркер
Получение обрабатывающего автомата из распознающего

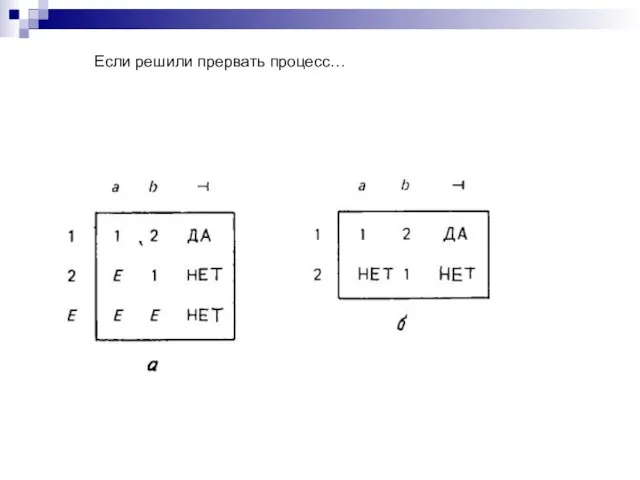
Если решили прервать процесс…

Лексический анализ входного языка транслятора (работа по курсу «Теория вычислительных процессов и структур»)

Процесс трансляции с алгоритмического языка можно условно разбить на три этапа:
лексический анализ, грамматический разбор и генерацию машинного кода.
Рассмотрим задачу построения лексического анализатора входного текста транслятора.

Лексический анализ
Под лексическим анализом понимают процесс предварительной обработки исходной программы, на котором основные лексические единицы программы - лексемы: ключевые слова, идентификаторы, метки, константы приводятся к единому формату и заменяются условными кодами или ссылками на соответствующие таблицы, а комментарии исключаются из текста программы.
Результатом лексического анализа является список лексем-дескрипторов и таблицы. В таблицах хранятся значения выделенных в программе лексем.

Дескриптор
Дескриптор- это пара вида: ( . < указатель>), где - это, как правило, числовой код класса лексемы, который означает, что лексема принадлежит одному из конечного множества классов слов, выделенных в языке программирования;
- это может быть либо начальный адрес области основной памяти, в которой хранится адрес этой лексемы, либо число, адресующее элемент таблицы, в которой хранится значение этой лексемы.

После проведения успешной идентификации лексемы формируется её образ
- дескриптор, он помещается в выходные данные лексического анализатора. В случае неуспешной идентификации формируется сообщение об ошибках в написании слов программы.
В ходе лексического анализа могут выполняться и другие виды лексического контроля, в частности, проверяться парность скобок и других парных символов, наличие метки у оператора, следующего за GOTO и т.д.
Результаты работы сканера передаются в последствии на вход синтаксического анлизатора. Имеется две возможности их связи: раздельная связь и нераздельная связь.

PROGRAM PRIMER;
VAR X,Y,Z : REAL;
BEGIN
X:=5;
Y:=6;
Z:=X+Y;
END;
Применим следующие коды для типов лексем:
К1- ключевое слово;
К2- разделитель;
К3- идентификатор;
К4- константа.

Лексический анализ можно производить, если нам задан алфавит, список ключевых слов языка и служебных символов.
Пусть всё это имеется. Тогда внутренние таблицы сканера примут следующий вид.

На основании составленных таблиц можно записать входной текст через введённые дескрипторы (дескрипторный текст):
( К1, 1) (К3, 1) (K2, 1)
( K1, 6) (K3, 2) (K2, 2) (k3, 3) ( K2, 2) (K3, 4) ( K2, 7) (K1, 5) (K2,
1)
( K1, 2)
( K3, 2) (K2, 7) (K2, 8) (K4, 1) (K2, 1)
( K3, 3) (K2, 7) (K2, 8) (K4, 2) (K2, 1)
( K3, 4) (K2, 7) (K2, 8) (K3, 2) (K2, 3) (K3, 3) (K2, 1)
( K1, 3) (K2, 9).

Схемы программ
Схема программ— математическая модель программ, в которой такие понятия, как оператор, операнд, переменная, выполнение и т.д., являются обобщением соответствующих понятий существующих языков программирования. Понятие схемы программы принадлежит советскому математику А.А.Ляпунову, которое он ввел в 1953г., исходя из общей концепции необходимости и возможности формализации процесса программирования. В настоящее время теория схем программ — это широко разветвленная область исследования, которая имеет многочисленные выходы в практику программирования и содержит фундаментальные результаты не только по операторным методам программирования, определившим современное состояние автоматизации программирования, но и по признаваемым перспективными методам рекурсивного и параллельного программирования.

Стандартные схемы
Стандартные схемы — схемы алголоподобных программ, исследование которых составляет основное содержание общей теории схем программ.
Стандартные схемы учитывают разбиение памяти на переменные и позволяют исследовать более широкий класс преобразований программ, включающий уже и такие преобразования, как, например, экономия общих подвыражений.
Стандартные схемы запрещают структурность операторов и переменных и, таким образом, моделируют лишь узкий класс реальных программ. Каждый оператор в такой схеме является либо преобразователем — оператором, изменяющим состояние памяти, либо распознавателем — оператором, осуществляющим выбор для исполнения одного из нескольких своих преемников. Преобразователь содержит одно обязательное присваивание и имеет одну исходящую дугу, а распознаватель не содержит присваиваний и имеет две исходящие дуги, одна из которых называется плюс-стрелкой (или 1-дугой), а вторая — минус-стрелкой (или 0-дугой).

Доказательство правильности программ
Принцип математической индукции
Принцип простой индукции
Обычно математическую индукцию вводят как метод доказательства утверждений о положительных числах.
Пусть S(n) — некоторое высказывание о целом числе n и требуется доказать, что S(n) справедливо для всех положи­тельных чисел n.
Согласно простой математической индукции, для этого необходимо
1. Доказать, что справедливо высказывание S(1).
2. Доказать, что если для любого положительного числа n справедливо высказывание S(n), то справедливо и высказы­вание S(n +1).

Принцип модифицированной простой индукции
Иногда необходимо доказать, что высказывание S(n) справедливо для всех целых n≥n0. Для этого можно довольно легко модифицировать принцип простой индукции. Чтобы доказать, что высказывание S(n) справедливо для всех целых n, необходимо:
1. Доказать, что справедливо S(n0).
2. Доказать, что если S(n) справедливо для всех целых n≥n0, то справедливо и S(n+1).

ПРИМЕР. Для любого неотрицательного числа n доказать, что
20 + 21 + 22 + … + 2n = 2n+1 – 1.
Используя простую индукцию, мы должны
1. Доказать, что 20 = 20+1 – 1. Это очевидно, так как
20 = 1 = 20+1 – 1 = 21 – 1= 2 – 1 = 1.
2. Доказать, что если для всех неотрицательных целых n справедлива формула
20 + 21 + 22 + … + 2n = 2n+1 – 1,
то справедлива и формула
20 + 21 + 22 + … + 2n + 2n+1 = 2(n+1)+1 – 1.
Высказывание 20 + 21 + 22 + ... + 2 n = 2n+1 – 1 называется гипотезой индукции. Второе положение доказывается следующим образом:
20 + 21 + 22 + … + 2n + 2n+1 = (20 + 21 + 22 + … + 2n ) + 2n+1 =
= (2n+1 – 1) + 2n+1 = ( 2n+1 + 2n+1 ) – 1 =2⋅2n+1 – 1 = 2n+2 – 1 = 2(n+1)+1 – 1.
(По гипотезе индукции)
Что и требовалось доказать.
Поскольку мы доказали справедливость двух утвержде­ний, то по индукции формула
20 + 21 + 22 + … + 2n = 2n+1 – 1.
считается справедливой для любого неотрицательного числа n.

Иногда нужно доказать справедливость высказывания S(n) для целых n, удовлетворяющих условию n0≤n≤m0. Так как между n0 и m0 находится конечное число целых чисел, то справедливость S(n) можно доказать простым перебором всех возможных вариантов. Однако легче, а иногда и необходимо (если, например, мы не знаем конкретных значений n0 и m0) доказать S(n) по индукции. В этом случае можно воспользоваться одним из двух вариантов индукции
Простая нисходящая индукция
1. Доказать, что справедливо S(n0)
2. Доказать, что если справедливо S(n), то для любых целых n0 ≤ n ≤ m0–1 справедливо и S(n + 1).
Простая восходящая индукция
1. Доказать, что справедливо S(m0).
2. Доказать, что если справедливо S(n), то для любых целых n0+1≤n≤m0 справедливо и S(n – 1).
Интуитивно понятно, что этого достаточно для доказательства справедливости S(n) при любых n, удовлетворяющих условию n0 ≤n≤m0.

ДОКАЗАТЕЛЬСТВО ПРАВИЛЬНОСТИ
БЛОК-СХЕМ ПРОГРАММ
Если мы хотим доказать, что некоторая программа правильна или верна, то прежде всего должны уметь описать то, что по предположению делает эта программа. Назовем такое описание высказыванием о правильности или просто утверждением и свяжем его с точкой на блок-схеме, предшествующей блоку останова STOP. В этом случае доказательство правильности состоит из доказательства того, что программа, будучи запущенной, в конце концов окончится (выполнится оператор STOP), и после окончания программы будет справедливо утверждение о правильности. Часто требуется, чтобы программа работала правильно только при определенных значениях входных данных. В этом случае доказательство правильности состоит из доказательства того, что если программа выполняется при соответствующих входных данных, то она когда-либо закончится, и после этого будет справедливо утверждение о правильности.

Высказывание о входных данных
Утверждение, относящееся к данным (или высказывание о входных данных), описывающее ограничение на входные данные программы, приписывается точке блок-схемы сразу после начала (блок START) или ввода исходных данных.

Инвариант цикла

Инвариант цикла
Под инвариантом цикла будем понимать утверждение, связывающее переменные, изменяющиеся внутри тела цикла, которое принимает значение истинно при входе в цикл, при каждой итерации цикла и после окончания цикла. Данный факт отображается в логическом комментарии, который называется комментарием инвариантного отношения и приписывается к точке начала цикла.

Конечность цикла
Кроме того, припишем к этой же точке ключевое утверждение о конечности цикла, в котором говорится, что в конце концов мы попадем в эту точку со значениями переменных, обуславливающих прекращение выполнения тела цикла.

При доказательстве правильности блок-схем являются:
1) доказательство того, что при попадании во входную точку цикла всегда будет справедливо некоторое утверждение (инвариант цикла). Чтобы доказать это, мы показывали, во-первых, что это утверждение справедливо при первом попадании на вход цикла, и, во-вторых, если мы попали в эту точку и утверждение справедливо, то после выполнения цикла и возврата во входную точку утверждение будет оставаться справедливым;
2) доказательство того, что при одновременном выполнении утверждения, являющегося инвариантом цикла и утверждения о конечности цикла из инварианта цикла автоматически следует утверждение о правильности программы.

ПРИМЕР 2. Предположим, что нужно вычислить произведение двух любых целых чисел M, N, причем M≥0 и операцию умножения использовать нельзя. Для этого можно использовать операцию сложения и вычислить сумму из M слагаемых (каждое равно N). В результате получим M∙N. Рассмотрим блок-схему, реализующую такое вычисление. Нужно доказать, что приведенная программа правильно вычисляет произведение двух любых целых чисел M и N при условии M≥0, т. е. если программа выполняется с целыми числами M и N, где M≥0, то она в конце концов окончится (достигнув точки 5) со значением J=M∙N.

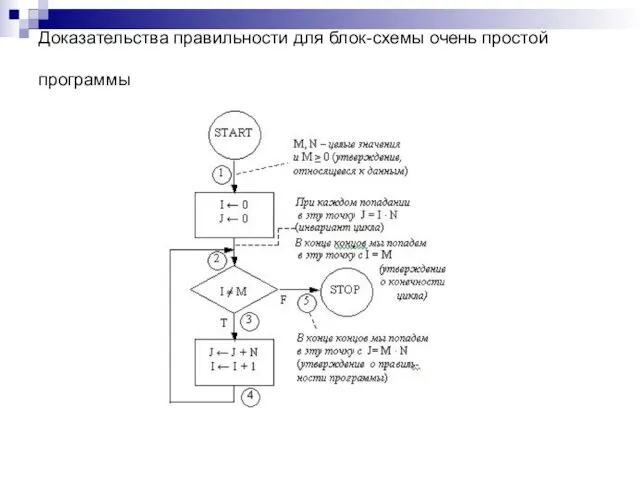
Доказательства правильности для блок-схемы очень простой программы

Докажем теперь, что приведенная на рис. блок-схема правильна, т. е. если ее начать выполнять с M и N, имеющими некоторые целые значения, причем M≥0, то выполнение в конечном итоге закончится с J = M ∙ N.
Вначале докажем, что при попадании в точку 2 J = I ∙ N.
1. При первом попадании в точку 2 при переходе из точки 1 имеем I = 0 и J = 0. Таким образом, утверждение J = I ∙ N = 0 ∙ N = 0 справедливо.

МЕТОД ИНДУКТИВНЫХ УТВЕРЖДЕНИЙ
При доказательстве правильности программ методом индуктивных утверждений доказательство конечности программы проводится отдельно от доказательства справедливости некоторых ключевых утверждений при достижении соответствующих точек программы.
Причем сначала необходимо доказать конечность программы, а после этого уже доказывать ее правильность, применяя метод индуктивных утверждений.

Пусть A – некоторое утверждение, описывающее предполагаемые свойства данных в программе (блок-схеме), а C – утверждение, описывающее то, что мы по предположению должны получить в результате процесса выполнения программы (т. е. утверждение о правильности). Будем говорить, что программа правильна (по отношению к A и С), если программа заканчивается при всех данных, удовлетворяющих A, и каждом выполнении ее с данными, удовлетворяющими предположению A, будет справедливо утверждение С.

Метод индуктивных утверждений
Свяжем утверждение A с началом программы, а утверждение С – с конечной точкой программы. Кроме этого, выявим некоторые закономерности, относящиеся к значениям переменных, и свяжем соответствующие утверждения с другими точками программы. В частности, свяжем такие утверждения по крайней мере с одной из точек в каждом из замкнутых путей в программе (в циклах). Для каждого пути в программе, ведущего из точки i, связанной с утверждением Ai, в точку j, связанную с утверждением aj (при условии, что на этом пути нет точек с какими-либо дополнительными утверждениями), докажем, что если мы попали в точку i и справедливо утверждение Аi, а затем прошли от точки i до точки j, то при попадании в точку j будет справедливо утверждение aj. Для циклов точки i и j могут быть одной и той же точкой.

Конечность программы
Сначала надо удостовериться, что программа закончится. Отметим, что единственными местами в программе, где изменяются I и J, являются «изолирован­ные» части двух итерационных блоков, управляющие увели­чением параметра цикла. Так как значение J увеличивается на 1, а значение N при выполнении внутреннего цикла не изменяется (путь через точки 3, 4, 5, 3 или через точки 3, 4, 6, 3), то значение J должно в конце концов превы­сить значение N. Таким образом, попадая в точку 3, мы когда-нибудь (после конечного числа выполнений внутрен­него цикла) должны попасть в точку 7, а затем в точку 2, При каждом попадании в точку 2 мы затем попадем либо в точку 8, и процесс закончится, либо в точку 3. Если мы попали в точку 3, мы только что видели, как в конце концов дойдем до точки 7 и вернемся в точку 2. При этом зна­чение I будет увеличиваться на 1, а значение M останется неизменным. Следовательно, после конечного числа шагов значение I станет больше значения M. В этот момент мы перейдем из точки 2 в точку 8, и программа закончится. Таким образом, мы доказали конечность нашей программы.

Для доказательства правильности рассмотрим все пути
1. Путь из точки 1 в точку 2. Предположим, что мы находимся в точке 1 и связанное с ней утверждение справедливо, т. е. данные удовлетворяют исходному допущению. Перейдем из точки 1 в точку 2. Нужно показать, что после прихода в точку 2 связанное с этой точкой утверждение будет справедливо. Если мы попали в точку 2 из точки 1, то имеем I = 1 и XLGST = X1,1. Так как M≥1, то очевидно, что 1 ≤ (I=1) ≤ M+1. Поскольку XLGST = X1,1 и I=1, то утверждение о XLGST справедливо.

2. Путь из точки 2 в точку 3. Предположим, что мы находимся в точке 2 и справедливо связанное с нею утверждение. Перейдем из точки 2 в точку 3. Требуется показать, что при попадании в точку 3 будет справедливо утверждение, связанное с этой точкой. Если мы дошли до точки 3 (из точки 2), то имеем J = 1, а значение XLGST осталось неизменным. Так как N≥1, 1 ≤ (J=1) ≤ N+1, а значение I после точки 2 не изменялось, то 1 ≤ I ≤ M + 1. Однако если мы пришли из точки 2 в точку 3, то известно, что проверка 1≤M была истинной, и, комбинируя это отношение с 1 ≤ I ≤ M + 1, получаем 1 ≤ I ≤ M. Если I = 1и J = 1, то из утверждения 2 получим XLGST = X1,1. В противном случае (т.е. при I≠1) из утверждения 2 получаем, что XLGST равно максимальному из значений элементов в первых I–1 строках массива X или, более точно, максимальному из значений элементов в первых I–1 строках и из значений первых J–1 = 1–1 = 0 элементов в I-й строке. Таким образом, очевидно, что при переходе из точки 2 в точку 3 утверждение, связанное с точкой 3, оказывается справедливым.

3. Путь из точки 3 через точки 4, 5 к точке 3. Предпо­ложим, что мы находимся в точке 3 и справедливо утверж­дение, связанное с этой точкой. Пройдем через точки 4, 5 к точке 3. Нужно показать, что при возврате в точку 3 соответствующее утверждение останется справедливым. Пусть I и J в исходном положении в точке 3 принимают значения In и Jn. Мы имеем 1 ≤ In ≤ M и
1 ≤ Jn ≤ N+1. При возврате в точку 3 через точки 4 и 5 получим In+1 = In и
Jn+1 = Jn + 1. Следовательно, опять имеем 1 ≤ In+1 = In ≤ M. Если мы проходим по этому пути, то проверка Jn ≤ N была истинной. Из этого, а также из соотношения 1 ≤ Jn ≤ N+1 получаем 1 ≤ Jn ≤ N. Таким образом, при возврате в точку 3 снова имеем 1 < (Jn+1 = Jn + 1) ≤ N+1. На всем пути перехода в точку 3 значение XLGST не изменялось, и известно, кроме того, что истинна проверка
≤ XLGST. Если учесть истинность утверждения о XLGST до «прохода» по указанному пути, то данное утверждение остается истин­ным и при возврате в точку 3 с In+1 = In и Jn+1 = Jn + 1. Так как ≤ XLGST, то неизменное значение XLGST снова будет максимальным из значений элементов в первых
In+1 – 1 = In – 1 строках и из значений первых Jn+1 – 1 = (Jn + 1) – 1 = Jn элементов в In-й строке массива X.

4. Путь из точки 3 через точки 4, 6 в точку 3. Рассужде­ния для этого пути аналогичны приведенным для предыдущего пути, за исключением того, что при возврате в точку 3 XLGST будет иметь значения . Кроме того, так как выбран этот путь, проверка ≤ XLGST была ложной и, следова­тельно, XLGST < . Таким образом, больше максимального из значений элементов первых In – 1 строк и Jn – 1 элементов в In-й строке. Отсюда следует, что при возврате в точку 3 значение XLGST остается максимальным из значений элементов первых In+1 – 1 = In – 1 строк и первых Jn+1 – 1 = (Jn + 1) – 1 = Jn элементов в In+1 = In-й строке массива X.

5. Путь из точки 3 через точку 7 в точку 2. Предполо­жим, что мы находимся в точке 3 и справедливо соответ­ствующее утверждение. Перейдем из точки 3 через точку 7 в точку 2. Нужно показать, что при возврате в точку 2 будет справедливо связанное с нею утверждение. Из точки 3 в точ­ку 7 мы попадем только тогда, когда ложна проверка J ≤ N. Но из утверждения, относящегося к точке 3, известно, что 1 ≤ J ≤ N+1. Отсюда можно заключить, что J = N+1. Пусть I в точке 3 принимает значение In. Утверждение в точке 3 гласит:
1 ≤ In ≤ M и XLGST равно максимальному из зна­чений элементов в первых
In – 1 строках и первых J – 1 = (N + 1) – 1 = N элементов в In-й строке массива X. Но так как в массиве X существует только N столбцов, то XLGST равно максимальному из значений элементов в In строках массива X. Значение XLGST между точками 3 и 2 не изменялось, а значение I изменилось и стало равным I + 1. Так как в точке 3 было справедливо отношение 1≤ In ≤ M, то это означает, что
1 < (In+1 = In + 1) ≤ M + 1 справедливо в точке 2. Следовательно, при достижении точки 2 будет справедливо утверждение: XLGST равно максимальному из значений элементов в первых I – 1 = (In + 1) – 1 = In строках массива X.

6. Путь от точки 2 в точку 8. Предположим, что мы находимся в точке 2, справедливо соответствующее утверж­дение и мы переходим в точку 8. Необходимо показать, что при достижении точки 8 будет справедливо связанное с нею утверждение. Из точки 2 мы перейдем в точку 8, если была ложной проверка
I ≤ M. Однако в точке 2 было справедливо неравенство 1≤ I ≤ M+ 1; следовательно, можно заключить, что I= M+1. Значение XLGST при переходе из 2 в 8 не изменялось, и, таким образом, из утверждения, относящегося к точке 2, можно заключить, что при попадании в точку 8 XLGST равно максимальному из значений эле­ментов в первых I – 1 = (M + 1) – 1 = M строках массива X. Но массив X содержит только M строк; следовательно, XLGST равно максимальному из значений элементов X.
Если объединить это доказательство с предыдущим доказательством конечности программы, то отсюда следует полная правильность программы.

Основной метод при доказательстве правильности рекурсивных программ называется методом структурной индукции.
F(Х1, ... , ХN) ≡ IF проверка 1 THEN выражение 1
ELSE IF проверка 2 THEN выражение 2
:
ELSE IF проверка m THEN выражение m
ELSE OTHERWISE выражение m + 1
Такая программа вычисляет значение F(Х1,... , ХN).
функция F, определяемая в нашей программе, может входить как часть в любое из выра­жений или проверок в программе. Такое появление F называется рекурсивным обращением к этой функции. Для каждой такой рекурсивной программы нужно еще указать, для каких значений аргументов X1, ... , ХN применима программа, т. е. нужно задать область определения функции. Выполнение программы заключается в применении ее к некоторым конкретным данным из ее области определения.

Пример 7.1. Рассмотрим рекурсивную программу, определенную для любого положительного целого числа X:
F(Х) ≡ IF Х = 1 THEN 1
ELSE OTHERWISE X•F(Х–1)
Чтобы понять, как работает такая программа, выполним ее для некоторого конкретного значения аргумента X. Например,
F(4) = 4 • F(3) [Так как условие 4 = 1 ложно, то F(4)=4•F(3).
Теперь нужно вычислить F(3), т.е. рекурсивно
обратиться к F.]
= 4 • 3 • F(2) [Так как при вычислении F(3) условие 3 = 1 ложно,
то F(3) = 3•F(2).]
= 4 • 3 • 2 • F(1) [Так как условие 2 = 1 ложно, то F(2) = 2•F(1).]
= 4 • 3 • 2 • 1 [Так как условие 1 = 1 истинно, то F(1) = 1.]
= 24 = 4 !
Далее мы докажем, что F(Х) = Х! для любого положительного целого числа X.

Чтобы сделать наш язык программирования точным, нам нужно задать правила вычислений для программ, определяющие последовательность вычислений. Будем считать, что правило вычислений отдает предпочтение самому левому и самому внутреннему обращению. Другими словами, в любой из моментов вычислений первым начинает вычисляться левое и внутреннее обращение (для простоты далее везде будем опускать слово «самое») к функции F, все аргументы которой уже не содержат F. Это правило – не обязательно наилучшее, иногда оно может приводить к неоканчивающейся последовательности вычислений, хотя другое правило дало бы конечную последовательность (пример 4.3). Однако во многих существующих языках программирования используется правило вычислений, подобное описанному выше. Кроме того, большинство рассматриваемых нами программ заканчивается при любых значениях аргументов независимо от того, какие правила вычислений мы используем, а следовательно, и результат в любых случаях будет одинаковым. Поэтому для определенности будем считать, что предпочтение отдается левому внутреннему обращению.

Структурная индукция
Рекурсивные программы обычно строятся по следующей схеме: сначала в них явно определяется способ вычисления результата для наипростейших значений аргументов рекурсивной функции, затем способ вычисления результата для аргументов более сложного вида, причем используется сведение к вычислениям с данными более простого вида (с аргументами рекурсивного обращения к той же функции). Таким образом, вполне естественно попытаться доказать правильность таких программ следующим образом:
1) доказать, что программа работает правильно для простейших данных (аргументов функции);
2) доказать, что программа работает правильно для более сложных данных (аргументов функции) в предположении, что она работает правильно для более простых данных (аргументов функции).
Такой способ доказательства правильности для рекурсивных функций естествен, поскольку он следует основной схеме вычислений в рекурсивных программах. Назовем его доказательством с помощью структурной индукции.

Докажем правильность рекурсивной программы:
F(Х) ≡ IF X = 1 ТНЕN 1
ЕLSЕ ОТНЕRWISЕ X•F(Х – 1)
Предполагается, что эта функция вычисляет факториал от аргумента. Нужно доказать, что F(М) = 1 • 2 • 3 • ... • N = N! для любого положительного числа N. При доказательстве с помощью структурной индукции используем простую индукцию по положительным целым числам:
1. Докажем, что F(1)= 1!. Действительно, F(1)= 1=1!.
2. Докажем (для любого положительного числа N), что если F(N) = 1 • 2 • ... • N = N!, то F(N + 1) = 1 • 2 • ... • N • (N + 1) = (N + 1)!. Следовательно, мы предполагаем, что N – положительное число, а F(N) = N! – гипотеза индукции. Так как N положительное число, то проверка N + 1 = 1 дает отрицательный ответ, и, прослеживая далее последовательность вычислений, получаем
F(N + 1) = (N + 1) • F((N + 1) – 1) = (N + 1) • F(N) =
= (N + 1) • ( N! ) = (N + 1) • (1 • 2 • ... • N) = 1 • 2 • ... • N • (N + 1) = (N + 1)!
(По гипотезе
индукции)
что и требовалось доказать, т. е. F(N) = N! для любого положительного числа N.