Содержание
- 2. 1775 - 1836
- 3. Учёный высказал гениальную идею: единственной причиной действия проводника с током на магнитную стрелку является движущееся электричество;
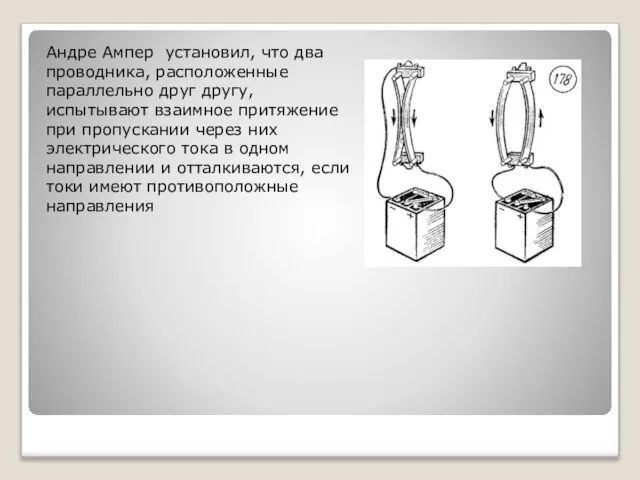
- 4. Андре Ампер установил, что два проводника, расположенные параллельно друг другу, испытывают взаимное притяжение при пропускании через
- 5. Явление взаимодействия электрических токов Ампер назвал электродинамическим взаимодействием. На основании своих опытов Ампер пришел к выводу,
- 6. Зако́н Ампе́ра — закон взаимодействия постоянных токов — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером
- 7. Направление силы определяется по правилу вычисления векторного произведенияопределяется по правилу вычисления векторного произведения, которое удобно запомнить
- 8. Два бесконечных параллельных проводника в вакууме Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В
- 9. В математической формулировке для магнитостатики теорема имеет[2]следующий вид[1][3]: Здесь — вектор магнитной индукцииЗдесь — вектор магнитной
- 10. Тогда теорема о циркуляции запишется в форме[6] где под (в отличие от в формуле выше) имеются
- 11. Данная теорема позволяет весьма просто находить величину магнитного поля во всём пространстве по заданным токам .
- 13. Скачать презентацию
Слайд 3Учёный высказал гениальную идею: единственной причиной действия проводника с током на магнитную
Учёный высказал гениальную идею: единственной причиной действия проводника с током на магнитную

Андре-Мари Ампер высказал гениальную идею: единственной причиной действия проводника с током на магнитную стрелку является движущееся электричество; магнетизм—лишь одно из его многочисленных проявлений. Не проводник, по которому течет ток, становится магнитом, а наоборот, магнит представляет собой совокупность токов. В магните есть множество элементарных круговых токов, текущих в плоскостях, перпендикулярных к его оси.
АВ — неподвижный проводник, ECDF — подвижный проводник, укрепленный на стеклянной оси EF.
Для зашиты от воздушных колебаний прибор накрыт стеклянным колпаком. (Рисунок Ампера).
Слайд 4Андре Ампер установил, что два проводника, расположенные параллельно друг другу, испытывают взаимное
Андре Ампер установил, что два проводника, расположенные параллельно друг другу, испытывают взаимное
Слайд 5Явление взаимодействия электрических токов Ампер назвал электродинамическим взаимодействием.
На основании своих опытов Ампер
Явление взаимодействия электрических токов Ампер назвал электродинамическим взаимодействием. На основании своих опытов Ампер
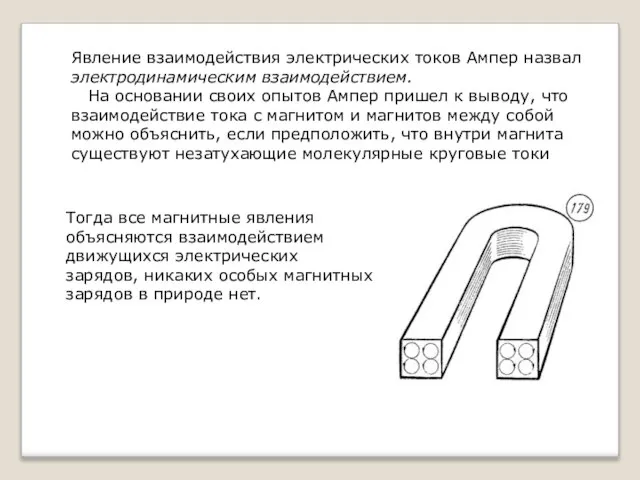
Тогда все магнитные явления объясняются взаимодействием движущихся электрических зарядов, никаких особых магнитных зарядов в природе нет.
Слайд 6Зако́н Ампе́ра — закон взаимодействия постоянных токов — закон взаимодействия постоянных токов.
Зако́н Ампе́ра — закон взаимодействия постоянных токов — закон взаимодействия постоянных токов.

.
Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный dl и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :
.
Слайд 7Направление силы определяется по правилу вычисления векторного произведенияопределяется по правилу вычисления векторного
Направление силы определяется по правилу вычисления векторного произведенияопределяется по правилу вычисления векторного

Модуль силы Ампера можно найти по формуле:
,
где α — угол между векторами магнитной индукции и тока.
Сила dF максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции
.
Слайд 8
Два бесконечных параллельных проводника в вакууме
Наиболее известным примером, иллюстрирующим силу Ампера,
Два бесконечных параллельных проводника в вакууме
Наиболее известным примером, иллюстрирующим силу Ампера,

Бесконечный проводник с током I1 в точке на расстоянии r создаёт магнитное поле с индукцией:
(по закону Био — Савара — Лапласа).
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).
Модуль данной силы (r — расстояние между проводниками):
Интегрируем, учитывая только проводник единичной длины (пределы l от 0 до 1):
Два параллельных проводника
Слайд 9В математической формулировке для магнитостатики теорема имеет[2]следующий вид[1][3]:
Здесь — вектор магнитной индукцииЗдесь
В математической формулировке для магнитостатики теорема имеет[2]следующий вид[1][3]:
Здесь — вектор магнитной индукцииЗдесь
![В математической формулировке для магнитостатики теорема имеет[2]следующий вид[1][3]: Здесь — вектор магнитной](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/443183/slide-8.jpg)
Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса[5].
Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики) и магнитные моменты понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики) и магнитные моменты микрочастиц (см.например ферромагнетики).
Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения (см. связанные токиПоэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения (см. связанные токи), выразив его через величину намагниченности I и введя вектор напряжённости магнитного поля
Слайд 10Тогда теорема о циркуляции запишется в форме[6]
где под (в отличие от в
Тогда теорема о циркуляции запишется в форме[6]
где под (в отличие от в
![Тогда теорема о циркуляции запишется в форме[6] где под (в отличие от](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/443183/slide-9.jpg)
В динамическом случае - то есть в общем случае классической электродинамики - когда поля меняются во времени (а в средах при этом меняется и их поляризация) - и речь тогда идет об обобщенной теореме, включающей , - всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене
Слайд 11
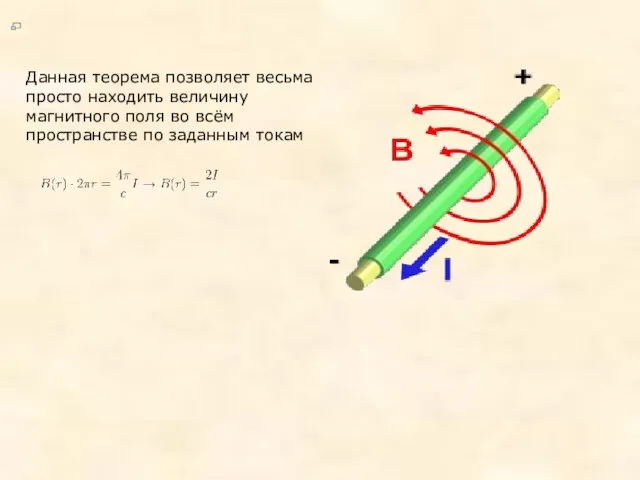
Данная теорема позволяет весьма просто находить величину магнитного поля во всём
Данная теорема позволяет весьма просто находить величину магнитного поля во всём
.

 Занятие 14
Занятие 14 Тест на математическое мышление
Тест на математическое мышление Японское чаепитие
Японское чаепитие CAF – 15 ЛЕТ В РОССИИ
CAF – 15 ЛЕТ В РОССИИ Erholungs- und Unterhaltungszentrum am Augustovski Kanal (Gebiet Grodno) mit einem Extrem-Park
Erholungs- und Unterhaltungszentrum am Augustovski Kanal (Gebiet Grodno) mit einem Extrem-Park Cтруктурно-функциональная организация генов и белков
Cтруктурно-функциональная организация генов и белков Развитие памяти у детей младшего школьного возраста на уроках литературного чтения
Развитие памяти у детей младшего школьного возраста на уроках литературного чтения Нормирование труда
Нормирование труда Архитектура компьютера
Архитектура компьютера Разработка электронного тренажера по интерактивной сборке ПК
Разработка электронного тренажера по интерактивной сборке ПК Викторина по рассказу А.И.Солженицына «Матрёнин двор»
Викторина по рассказу А.И.Солженицына «Матрёнин двор» « Работа с учебной литературой как способ формирования информационной культуры школьников на уроке биологии »
« Работа с учебной литературой как способ формирования информационной культуры школьников на уроке биологии » Презентация на тему Этапы рисования
Презентация на тему Этапы рисования  О пользе каши
О пользе каши Погода и её элементы
Погода и её элементы АНДРЕЙ РУБЛЕВ - ХУДОЖНИК ВОЛЕЙ БОЖЬЕЙ
АНДРЕЙ РУБЛЕВ - ХУДОЖНИК ВОЛЕЙ БОЖЬЕЙ Натюрморт
Натюрморт Памятка для участников проекта Старт в будущее от компании Лукойл
Памятка для участников проекта Старт в будущее от компании Лукойл Презентация на тему Природные ресурсы Арктики
Презентация на тему Природные ресурсы Арктики  Презентация на тему Статическая и динамическая механика легких
Презентация на тему Статическая и динамическая механика легких  Система занятий по истории славянской письменности как один из путей реализации культуроведческого подхода в преподавании русс
Система занятий по истории славянской письменности как один из путей реализации культуроведческого подхода в преподавании русс Развитие сети профессиональных юридических услуг в России и СНГ Альберт Еганян, к.ю.н., MCIArb, Управляющий партнер
Развитие сети профессиональных юридических услуг в России и СНГ Альберт Еганян, к.ю.н., MCIArb, Управляющий партнер Презентация на тему Охрана окружающей среды
Презентация на тему Охрана окружающей среды Тайна моего имени Кирилл
Тайна моего имени Кирилл Изучение риска злоупотребления психоактивных веществ
Изучение риска злоупотребления психоактивных веществ МОУ - ЮРЬЕВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛАХОТЫНЕЦКОГО РАЙОНА ОРЛОВСКОЙ ОБЛАСТИ Исследовательская работа«Влияние р
МОУ - ЮРЬЕВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛАХОТЫНЕЦКОГО РАЙОНА ОРЛОВСКОЙ ОБЛАСТИ Исследовательская работа«Влияние р Параллельность
Параллельность Презентация на тему Натуральные числа и шкалы
Презентация на тему Натуральные числа и шкалы