Архимед

Наше математическое состязание посвящено 300-летию со дня рождения
Михаила Васильевича Ломоносова

Желаем
удачи!

1
тур

1 ТУР ЗАДАЧА 1 УСЛОВИЕ:
Чашка кофе с кубиком сахара стоят 1 доллар 10 центов. Известно, что кофе дороже кубика сахара на 1 доллар. Сколько стоит само кофе, и сколько стоит кубик сахара?

1 ТУР ЗАДАЧА 1 РЕШЕНИЕ:
Переведем 1 доллар 10 центов в доллары – это 1,1 доллар
Пусть X долларов стоит кусочек сахара, тогда X + 1 стоит кофе
X + X+ 1 = 1,1
X = 0,05 (долларов)
Тогда кофе стоит 5 центов + 1 доллар, т.е.
1 доллар 5 центов.
Ответ: кофе стоит 1 доллар 5 центов, а кусочек сахара – 5 центов.
= 5 (центов)

У Ксюши было 80 копеек, а у Наташи – 64 копейки. Каждая из девочек захотела купить как можно больше одинаковых шоколадок. Ксюша получила 8 копеек сдачи, а Наташа – 10. Смогут ли девочки купить на эти деньги еще одну шоколадку?
1 ТУР ЗАДАЧА 2 УСЛОВИЕ:

1 ТУР ЗАДАЧА 2 РЕШЕНИЕ:
Ксюша купила шоколадки на 72 копейки, а Наташа – 54.
Шоколадка должна стоить больше 10 копеек, т.к. если бы цена шоколадки была бы менее 10 копеек, то Наташа бы смогла купить еще. 72 и 54 должны быть кратны цене шоколадки.
Следовательно, шоколадка стоит 18 копеек.
Сдача в сумме составляет 18 копеек, следовательно они смогут купить еще одну шоколадку.
Ответ: да, смогут

В забеге участвовали 11 спортсменов. Число спортсменов, прибежавших раньше Васи в 4 раза меньше, числа тех, кто прибежал позже него. Какое место занял Вася?
1 ТУР ЗАДАЧА 3 УСЛОВИЕ:

Пусть x - спортсменов прибежали раньше Васи.
x + 1 + 4x = 11
5x + 1= 11
5x= 10
x = 2
Следовательно, он занял 3-е место.
4x
x
Тогда 4x – спортсменов прибежали позже Васи.
1 ТУР ЗАДАЧА 3 РЕШЕНИЕ:

результаты
1
тур

1
тур
апелляция

2
тур

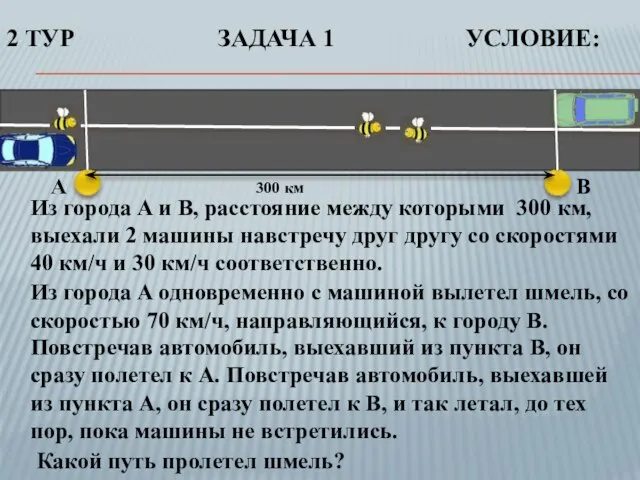
Из города A и B, расстояние между которыми 300 км, выехали 2 машины навстречу друг другу со скоростями 40 км/ч и 30 км/ч соответственно.
Из города A одновременно с машиной вылетел шмель, со скоростью 70 км/ч, направляющийся, к городу B.
Повстречав автомобиль, выехавший из пункта B, он сразу полетел к A. Повстречав автомобиль, выехавшей из пункта A, он сразу полетел к B, и так летал, до тех пор, пока машины не встретились.
Какой путь пролетел шмель?
A
B
300 км
2 ТУР ЗАДАЧА 1 УСЛОВИЕ:

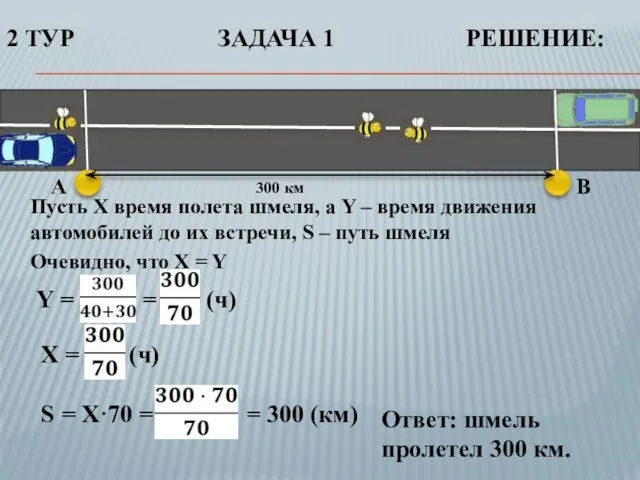
A
B
300 км
Пусть X время полета шмеля, а Y – время движения автомобилей до их встречи, S – путь шмеля
Очевидно, что X = Y
Y = = (ч)
X = (ч)
S = X·70 = = 300 (км)
Ответ: шмель пролетел 300 км.
2 ТУР ЗАДАЧА 1 РЕШЕНИЕ:

Как отмерить 15 мин. при помощи двух песочных часов, отмеряющих по 7 и 11 минут соответственно?
2 ТУР ЗАДАЧА 2 УСЛОВИЕ:

1) запустим одновременно часы на 11 и 7 минут.
2) когда кончится песок в часах на 7 минут, запустим отсчет искомых 15 минут.
3) когда выйдет время в часах на 11 минут, запустим заново часы на 11 минут.
4) когда выйдет время в часах на 11 минут, мы и получим искомые 15 минут.
2 ТУР ЗАДАЧА 2 РЕШЕНИЕ:
7
11
11
15
Начало отсчета

Больному дали 2 пары таблеток A и B, которые совершенно одинаковы на вид. Ему надо выпить по одной таблетке A и B утром, а потом еще и вечером. Что же ему сделать?
2 ТУР ЗАДАЧА 3 УСЛОВИЕ:

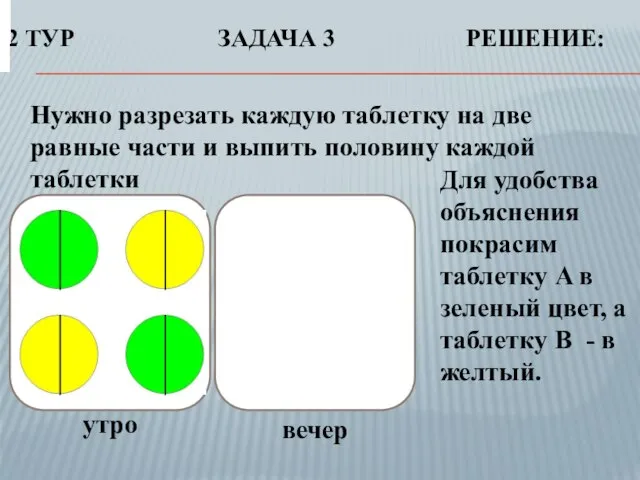
2 ТУР ЗАДАЧА 3 РЕШЕНИЕ:
Нужно разрезать каждую таблетку на две равные части и выпить половину каждой таблетки
Для удобства объяснения покрасим таблетку A в зеленый цвет, а таблетку B - в желтый.
утро
вечер

2
тур
результаты

2
тур
апелляция

3
тур

Имеется 30 бревен, длиной 3 и 4 метра, суммарная длина которых равна 100 метров. Сколько распилов нужно сделать, чтобы распилить бревна на куски длиной 1 метр?
3 ТУР ЗАДАЧА 1 УСЛОВИЕ:

3 ТУР ЗАДАЧА 1 РЕШЕНИЕ:
Составим уравнение:
Пусть X - количество бревен 3 метра длиной, а
(30 - X) – 4 метра длиной.
20·2 + 10·3
Ответ: нужно сделать 70 распилов
3·X + 4 ·(30 - X) = 100
X = 20
Следовательно, кол-во
четырёхметровых бревен – 10 штук
Чтобы распилить трёхметровое бревно на куски, длиной 1 метр, нужно сделать 2 распила, а четырёхметровое - 3
= 70

В неком государстве несколько городов. Из каждого города выходит по одной дороге в каждый из оставшихся городов. Сколько городов в этом государстве, если всего в нем 15 дорог?
3 ТУР ЗАДАЧА 2 УСЛОВИЕ:

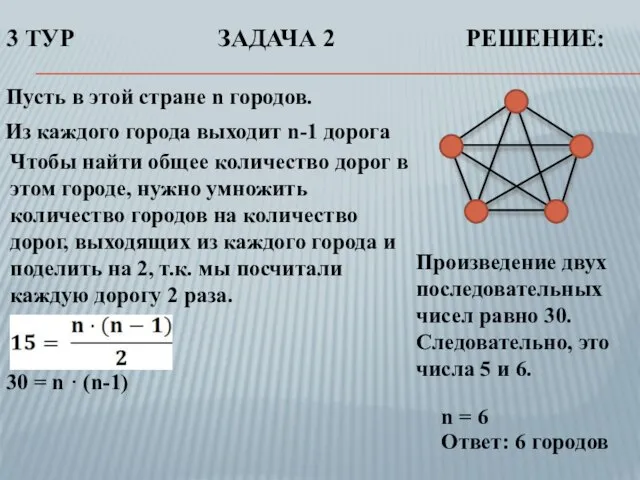
3 ТУР ЗАДАЧА 2 РЕШЕНИЕ:
Пусть в этой стране n городов.
Из каждого города выходит n-1 дорога
Чтобы найти общее количество дорог в этом городе, нужно умножить количество городов на количество дорог, выходящих из каждого города и поделить на 2, т.к. мы посчитали каждую дорогу 2 раза.
30 = n · (n-1)
n = 6
Ответ: 6 городов
Произведение двух последовательных чисел равно 30. Следовательно, это числа 5 и 6.

В магазине продается шоколад в виде букв английского алфавита. Разные буквы имеют различные цены, а одинаковые – одну и ту же. Известно, что слово ONE стóит 6$, слово TWO стóит 9$, а слово ELEVEN стóит 16$. Сколько будет стоить слово TWELVE?
3 ТУР ЗАДАЧА 3 УСЛОВИЕ:

3 ТУР ЗАДАЧА 3 РЕШЕНИЕ:
ONE стоит 6$; TWO стоит 9$; ELEVEN стоит 16$;
TWELVE = ?
O + N + E = 6$
T + W + O = 9$
E + L + E + V + E + N= 16$
3E + L + V + N= 16$
T + W + E + L + V + E = ?
2E + T + W + L + V= ?
E + L + E + V + E + N= 16$
3E + L + V + N= 16$
O + N + E = 6$
2E + L + V - O = 10$
T + W + O = 9$
2E + T + W + L + V= 19$
T + W + E + L + V + E = 19$
Ответ: 19$

3
тур
результаты

3
тур
апелляция

4
тур

В одном из двух городов живут все лжецы, а в другом – правдолюбы. И те и другие приезжают друг к другу в гости. Какой нужно поставить единственный вопрос прохожему, чтобы узнать, в каком городе вы находитесь?
4 ТУР ЗАДАЧА 1 УСЛОВИЕ:

4 ТУР ЗАДАЧА 1 РЕШЕНИЕ:
Нужно спросить: «вы здесь в гостях?» Если ответ «да», то вы в городе лжецов, а если «нет», то в городе правдолюбов.
II. Предположим, что вы в городе правдолюбов.
1)Если вы встречаете коренного жителя, т.е. правдолюба , он вам скажет правду и даст отрицательный ответ на вопрос.
2)Если вы встречаете приезжего, т.е. лжеца, он вам солжет и даст отрицательный ответ на ваш вопрос.
I. Предположим, что вы в городе лжецов.
1)Если вы встречаете коренного жителя, т.е. лжеца, он вам солжет и даст утвердительный ответ на вопрос.
2)Если вы встречаете приезжего, т.е. правдолюба, он вам скажет правду и даст утвердительный ответ на ваш вопрос.

На столе лежат десять пронумерованных шляп. В каждой шляпе лежит по десять золотых монет. В девяти шляпах настоящие и только в одной поддельные. Настоящая весит 10 грамм, а поддельная - 9. В помощь даны электронные весы, которые измеряют с точностью до грамма. Как за одно взвешивание определить в какой шляпе находятся фальшивые монеты?
4 ТУР ЗАДАЧА 2 УСЛОВИЕ:

1)Возьмем из первой шляпы 1 монету, из второй шляпы - 2 монеты, из 3 третьей – 3 монеты и т.д.
1
3
2
4
5
6
7
8
9
10
X ГРАММ
2)Предположим, что все эти монеты настоящие, тогда их масса равна 550 грамм.
3) Поместим все эти монеты на весы и определим общую массу монет.
4) Вычтем из общей массы в 550 грамм, массу, которую мы получили на весах, и если разница будет составлять 1 грамм, то фальшивые монеты в первой шляпе, если 2, то во второй и т.д.
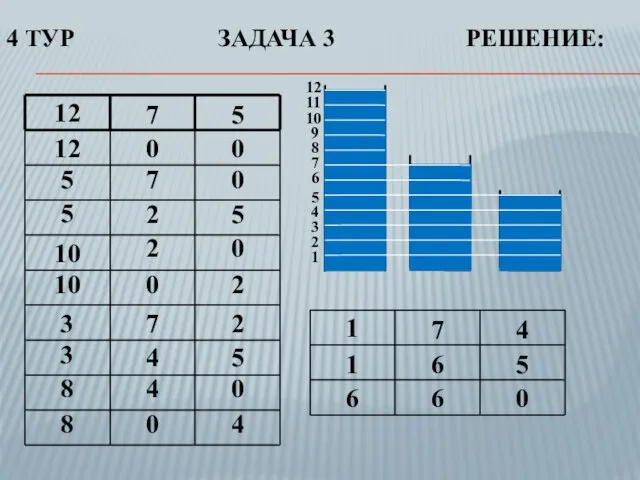
4 ТУР ЗАДАЧА 2 РЕШЕНИЕ:

Имеется 3 бочки по 12, 7, 5 литров. Бочка на 12 литров заполнена полностью, остальные – пустые. Как сделать так, чтобы в бочках по 7 и 12 литров оказалось по 6 литров воды?
4 ТУР ЗАДАЧА 3 УСЛОВИЕ:

4 ТУР ЗАДАЧА 3 РЕШЕНИЕ:
12
5
7
12
0
0
5
0
7
5
5
2
10
0
2
10
2
0
3
2
7
3
5
4
8
0
4
8
4
0
1
4
7
1
5
6
6
0
6
1
2
5
4
3
8
7
6
12
11
10
9

4
тур
результаты

4
тур
апелляция