Содержание
- 2. Цели исследования: Сформировать понимание необходимости знаний процентных вычислений для решения большого круга задач, показать широту применения
- 3. Задачи исследования: сформировать умения производить процентные вычисления, необходимые для применения в практической деятельности; решать основные задачи
- 4. Основополагающий вопрос Нужны ли проценты в современной жизни ? %
- 5. Темы исследований и процентных вычислений: История процентов «Распродажа» «Тарифы» «Штрафы» «Банковские операции» «Голосование» Проценты и ЕГЭ.
- 6. История процентов Слово «процент» происходит от латинского слова pro centum, что буквально означает «за сотню» или
- 7. История процентов Знак «%» происходит от итальянского слова cento (сто), которое в процентных расчетах часто писалось
- 8. История процентов В некоторых вопросах иногда применяют и более мелкие, тысячные доли, так называемые «промилле» (от
- 9. Задачи с историческими сюжетами Один небогатый римлянин взял в долг у заимодавца50 сестерциев. Заимодавец поставил условие:
- 10. Задачи с литературными сюжетами В романе М.Е. Салтыкова-Щедрина «Господа Головлевы» сын Порфирия Владимировича Петя проиграл в
- 11. Проценты и ЕГЭ Задача ЕГЭ для 9 класса Две фракции областной думы объединили 6о депутатов. При
- 12. Проценты и ЕГЭ. Задача ЕГЭ для 11 класса Агрофирма предполагает продать моркови на 10 % меньше,
- 14. Скачать презентацию











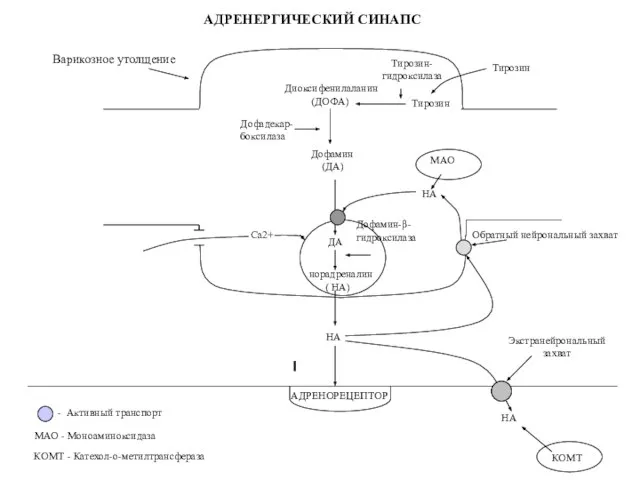 Адреномиметики
Адреномиметики Sport in Canada
Sport in Canada АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов
АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов Презентация на тему Русский герой сказок: Иван-дурак
Презентация на тему Русский герой сказок: Иван-дурак  Путешествие на водопад Атыш
Путешествие на водопад Атыш Помада Creamy Glam
Помада Creamy Glam Презентация по английскому Королевская семья Великобритании
Презентация по английскому Королевская семья Великобритании tema-gribi-rodnaya-tropinka_ru
tema-gribi-rodnaya-tropinka_ru Работа социального педагога с детьми имеющих отклоняющее поведение.
Работа социального педагога с детьми имеющих отклоняющее поведение. Комплекс упражнений утренней гимнастики
Комплекс упражнений утренней гимнастики Службы для электронного общения
Службы для электронного общения Характер и темперамент
Характер и темперамент Обществознание
Обществознание Материально-техническая база одно из условий эффективной реализации профильного обучения.
Материально-техническая база одно из условий эффективной реализации профильного обучения. Способ тепловой обработки сыпучих материалов и устройства для его осуществления
Способ тепловой обработки сыпучих материалов и устройства для его осуществления Архитектура Санкт-Петербурга
Архитектура Санкт-Петербурга project
project Greenway. Жизнь без химии с заботой о семье и природе
Greenway. Жизнь без химии с заботой о семье и природе Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16
Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16 Сказочные птицы
Сказочные птицы Леонардо Да Винчи
Леонардо Да Винчи Как преодолеть стресс перед экзаменом
Как преодолеть стресс перед экзаменом Признаки нарушения адаптации в почерке
Признаки нарушения адаптации в почерке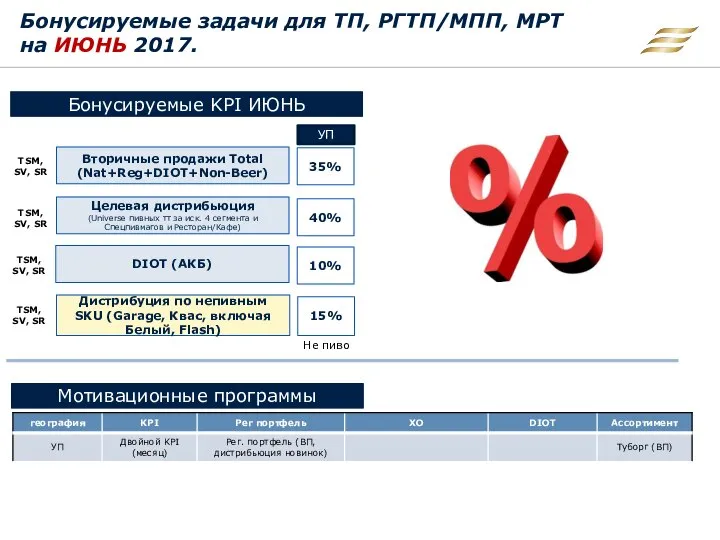 Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017
Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017 Доходы предприятия и финансовые результаты его деятельности
Доходы предприятия и финансовые результаты его деятельности Алтайский государственный университет
Алтайский государственный университет Методика оформление. Пушкинская карта
Методика оформление. Пушкинская карта Презентация на тему Социальная информатика
Презентация на тему Социальная информатика