AvB

Логика –
это наука о формах и способах мышления.

Содержание
Формы мышления
Алгебра высказываний
Логические выражения и таблицы истинности
Алгоритм построения таблиц истинности
Домашнее задание
Проверь себя

1. Формы мышления
Основные формы мышления:
Понятие
Высказывание
Умозаключение
содержание

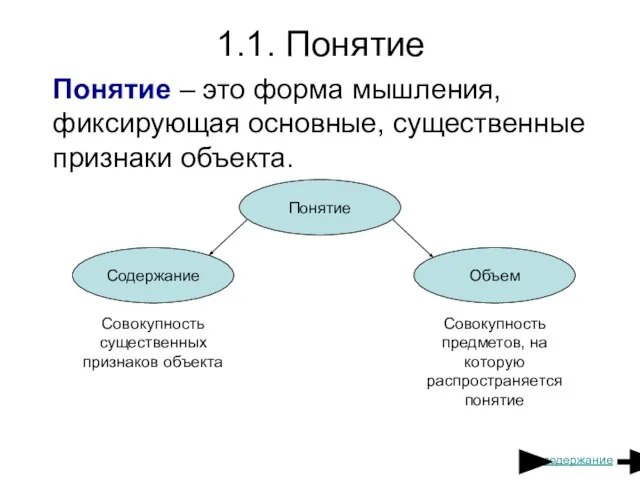
1.1. Понятие
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
Понятие
Содержание
Объем
Совокупность существенных признаков объекта
Совокупность предметов, на которую распространяется понятие
содержание

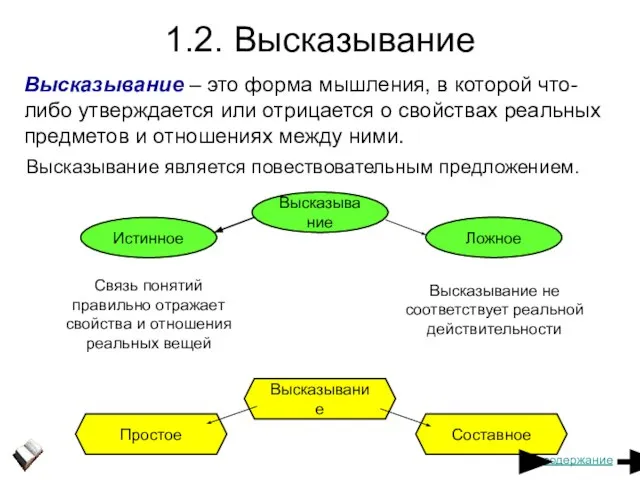
1.2. Высказывание
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними.
Высказывание является повествовательным предложением.
Высказывание
Истинное
Ложное
Связь понятий правильно отражает свойства и отношения реальных вещей
Высказывание не соответствует реальной действительности
Высказывание
Простое
Составное
содержание

Какие из предложений являются высказыванием?

1.3. Умозаключение
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).
Посылки – только истинные суждения.
содержание

2. Алгебра высказываний
Алгебра высказываний служит для определения истинности или ложности составных высказываний.
Высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0).
содержание

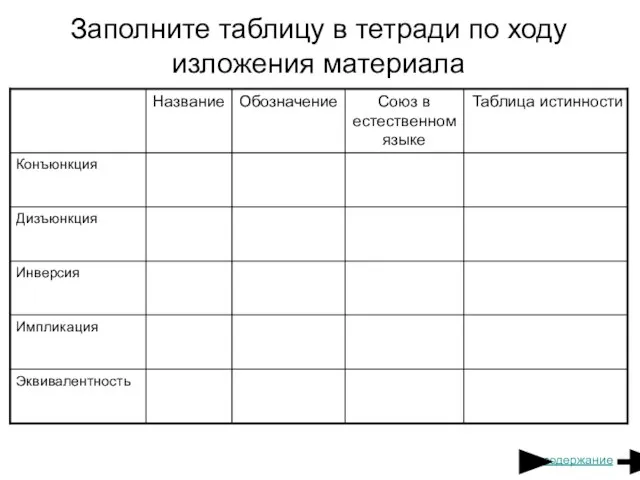
Заполните таблицу в тетради по ходу изложения материала
содержание

Логические операции
2.1. Логическое умножение (конъюнкция)
2.2. Логическое сложение (дизъюнкция)
2.3. Логическое отрицание (инверсия)
2.4. Логическое следование (импликация)
2.5. Логическое равенство (эквивалентность)
содержание

2.1. Логическое умножение (конъюнкция)
Объединение двух (или нескольких) высказываний в одно с помощью союза «и».
Составное высказывание истинно только тогда, когда истины оба простых высказывания.
Соответствует союзу И
Обозначение &, ^
В языках программирования and;
Таблица истинности
Логические
операции

2.2. Логическое сложение
(дизъюнкция)
Объединение двух (или нескольких) высказываний в одно с помощью союза «или».
Составное высказывание истинно только тогда, когда истинно хотя бы одно из двух простых высказывания.
Соответствует союзу ИЛИ
Обозначение V
В языках программирования or
Таблица истинности
Логические
операции

2.3. Логическое отрицание
(инверсия)
Присоединение частицы «не» к высказыванию.
Инверсия делает истинное высказывание ложным и, наоборот.
Соответствует союзу НЕ
Обозначение Ā, ¬А
В языках программирования not
Таблица истинности
Логические
операции

2.4. Логическое следование (импликация)
Соответствует обороту Если…, то…
Обозначение А→В
В языках программирования if … then …
Импликация образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».
Импликация ложна только тогда, когда из истинного первого высказывания(предпосылки) следует ложный вывод (второе высказывание).
Таблица истинности
Логические
операции

2.5. Логическое равенство
(эквивалентность)
Эквивалентность образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, когда …».
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Таблица истинности
Соответствует обороту тогда и только тогда, когда …
Обозначение А≡В, А~B
Логические
операции

3. Логические выражения и таблицы истинности
Логическое выражение – формула, в которую входят логические переменные Логическое выражение – формула, в которую входят логические переменные и знаки логических операций.
Пример:
Для логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний.
Порядок выполнения логических операций:
Действия в скобках.
Инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
содержание

Найдите значения логических выражений

4. Построение таблицы истинности
Определить количество строк в таблице по формуле 2n, где n – количество логических переменных.
Определить количество столбцов таблицы: количество логических переменных + количество логических операций.
Построить таблицу истинности, обозначить столбцы, внести всевозможные наборы исходных данных логических переменных.
Заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности.
содержание

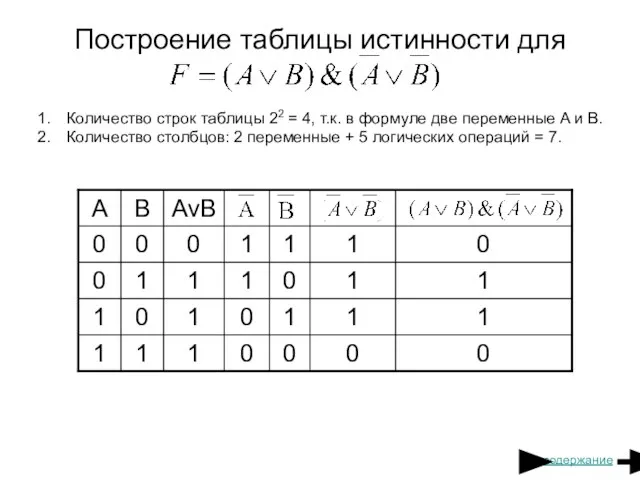
Построение таблицы истинности для
Количество строк таблицы 22 = 4, т.к. в формуле две переменные A и B.
Количество столбцов: 2 переменные + 5 логических операций = 7.
содержание

Равносильные логические выражения
Равносильные логические выражения - это выражения, у которых последние столбцы таблиц истинности совпадают, обозначают “=“.
Докажите равносильность выражений:
Таблица истинности для
Таблица истинности для
содержание

5. Домашнее задание
Даны высказывания:
A = «р делится на 5»
В = «р – нечетное число»
Найти множество значений р, при которых результат
а) дизъюнкции,
б) конъюнкции
будет:
истинным;
ложным.
содержание

Домашнее задание
2. Составьте и запишите истинные сложные высказывания из простых с использованием логических операций:
Неверно, что 10>Y>5 и Z<0.
Любое из чисел X, Y,Z положительно.
3. Составьте таблицу истинности для логического выражения:
F = (X & ¬Y) v Z
содержание

Проверь себя
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
содержание

Задание 1
Расставь соответствующие числа
Логика
Высказывание
Алгебра логики
Логическая константа
Дизъюнкция
Инверсия
Конъюнкция
Импликация
Эквивалентность
А → В
Логическое сложение
Наука о формах и способах мышления
Логическое отрицание
ИСТИНА и ЛОЖЬ
А ↔ В
&
Наука об операциях над высказываниями
Повествовательное предложение, в котором что-либо утверждается или отрицается
Правильных ответов:

Даны высказывания:
А = { 2 · 2 = 4 }
В = { 2 + 2 = 5 }
Определите истинность высказываний:
Задание 2
А
¬В
A & B
B
¬A
A v B
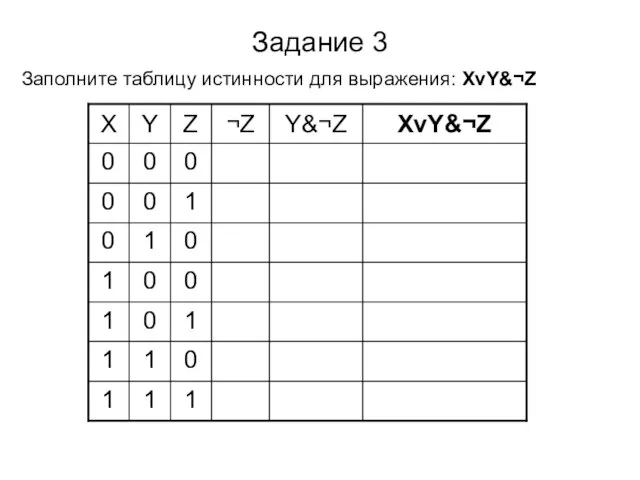
Правильных ответов:

Задание 3
Заполните таблицу истинности для выражения: XvY&¬Z

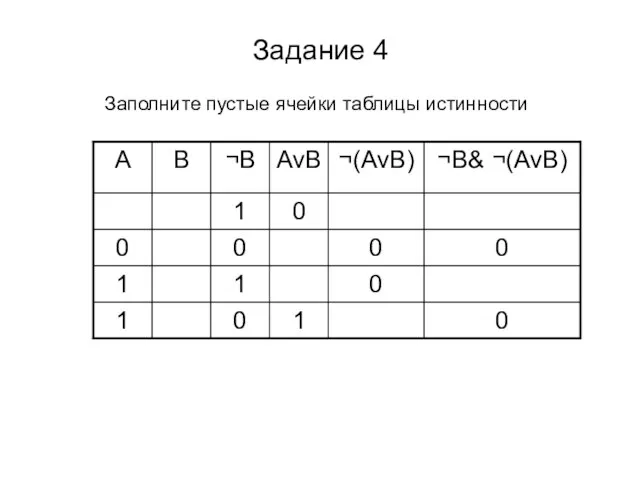
Задание 4
Заполните пустые ячейки таблицы истинности