Автоколебания в нелинейных АСУ

Методы исследования АК
Критерий Бендиксона -основан на том, что АК отсутствуют, если в фазовом портрете системы нет замкнутых фазовых траекторий.
Метод точечного преобразования А.Андронова используется для качественного исследования хода фазовых траекторий, выявления АК в системе и изучения их устойчивости.
Метод гармонического баланса (Л.С.Гольдфарб) основан на применении частотных характеристик нелинейной системы, получаемых в результате гармонической линеаризации, применяется для приближенного исследования.

Критерий Бендиксона
Область применения: для АСУ, описываемых системой нелинейных дифференциальных уравнений (НДУ):
dy1/dt = F1(y1,y2);
dy2/dt = F2(Y1,y2),
где F1( y1, y2 ) , F2 ( y1, y2 ) – нелинейные функции аналитические на всей фазовой плоскости.
Если в некоторой области на фазовой плоскости выражение ∂F1 / ∂y1 + ∂F2 / ∂y2 знакопостоянно, то в этой области не существует замкнутых фазовых траекторий (АК).

Пример: в химическом реакторе идеального перемешивания протекает химическая реакция, описываемая уравнениями:
где: y1 , y2 – текущие
концентрации реагентов в
реакторе;
y10 , y20 – начальные входные концентрации реагентов;
λ – расход; t – время.
Находим выражение:
∂F1 / ∂y1 + ∂F2 / ∂y2 = - 2 y1 - 2 λ - 1.
В соответствии с физическим смыслом y1 ≥ 0 , y2 ≥ 0 , т.е. концентрации не могут быть отрицательными, а также λ > 0 , последнее выражение представляет собой знакопостоянную отрицательную функцию, следовательно,
автоколебания существовать не могут.

Метод точечного преобразования А.Андронова
Система НДУ, описывающих поведение нелинейной АСУ:
1)
2)
Уравнение фазовой траектории получим, разделив уравнение 2) на уравнение 1):

При t →∞ фазовая траектория последовательно обходит начало координат. S* = Ψ(S) – функция последования для точечного преобразования отрезка 0-Γ в себя. Для каждой точки пересечения S она позволяет вычислить последующую точку пересечения S*. Зная S* = Ψ(S) и, приняв за начальную точку пересечения S0, можно вычислить:
Это итерационный процесс.
Особое значение имеют точки пересечения S,
которые преобразуются функцией Ψ в себя:
(*)
На отрезке «0-Γ» т.SN, является решением уравнения (*), и
называется неподвижной (или инвариантной) точкой
преобразования Ψ. Ее наличие свидетельствует об АК

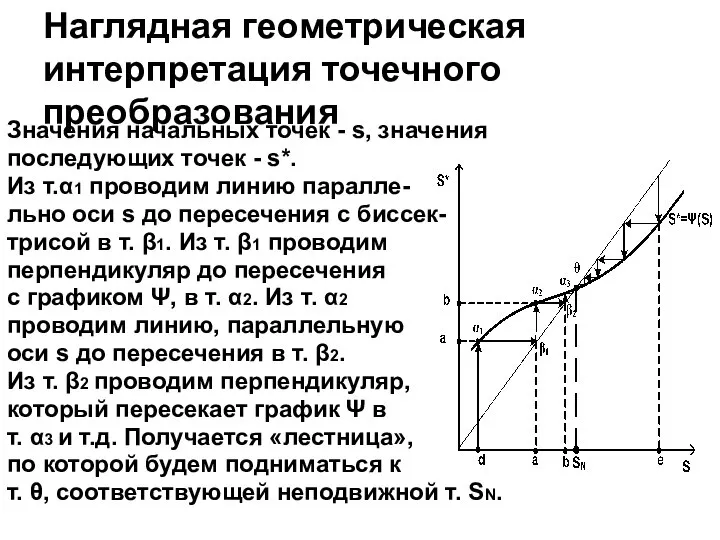
Наглядная геометрическая интерпретация точечного преобразования
Значения начальных точек - s, значения
последующих точек - s*.
Из т.α1 проводим линию паралле-
льно оси s до пересечения с биссек-
трисой в т. β1. Из т. β1 проводим
перпендикуляр до пересечения
с графиком Ψ, в т. α2. Из т. α2
проводим линию, параллельную
оси s до пересечения в т. β2.
Из т. β2 проводим перпендикуляр,
который пересекает график Ψ в
т. α3 и т.д. Получается «лестница»,
по которой будем подниматься к
т. θ, соответствующей неподвижной т. SN.

Если начальная т.S0 находится в т. е оси S, то, по лестнице спускаемся к точке θ.
Из рис. видно, что неподвижная т.SN может быть пределом последовательности итерационного процесса: (*)
т.SN – устойчива (устойчивые АК), если существует такая сколь угодно малая окрестность, что любая последова-тельность (*), начинающаяся в ней, сходится к т.SN. В противном случае неподвижная т.SN называется неустойчивой. «Лестница» на диаграмме это наглядно показывает.
Формальный критерий следующий:

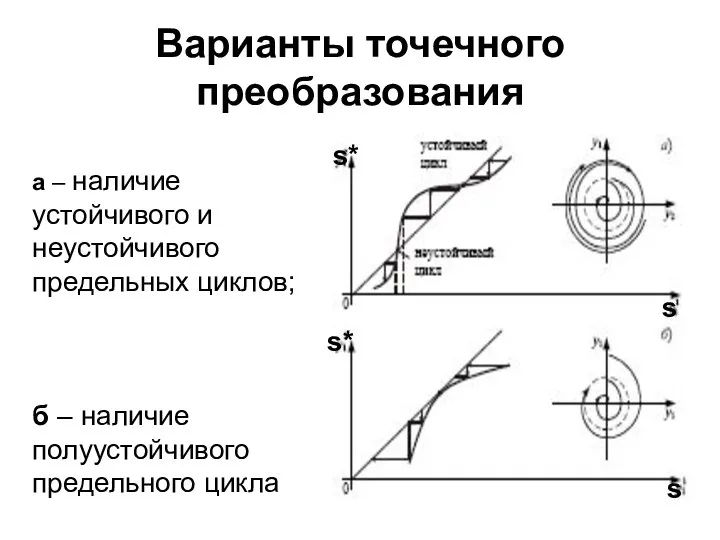
Варианты точечного преобразования
а – наличие устойчивого и неустойчивого предельных циклов;
б – наличие полуустойчивого предельного цикла
s
s
s*
s*

Метод гармонического баланса (Л.С.Гольдфарб)
Исходим из того, что: Нелинейная замкнутая АСУ состоит из линейной части, имеющей характеристику Wлч(iω) и объединяющей все линейные элементы системы, и нелинейного звена Yнэ = F (y );
нелинейный элемент не должен быть частото-преобразующим.
нелинейность может быть как статической, так и динамической.
линейная часть должна быть фильтром высоких частот.
Подобное упрощение для большинства промышленных систем регулирования не несет значительных ошибок.

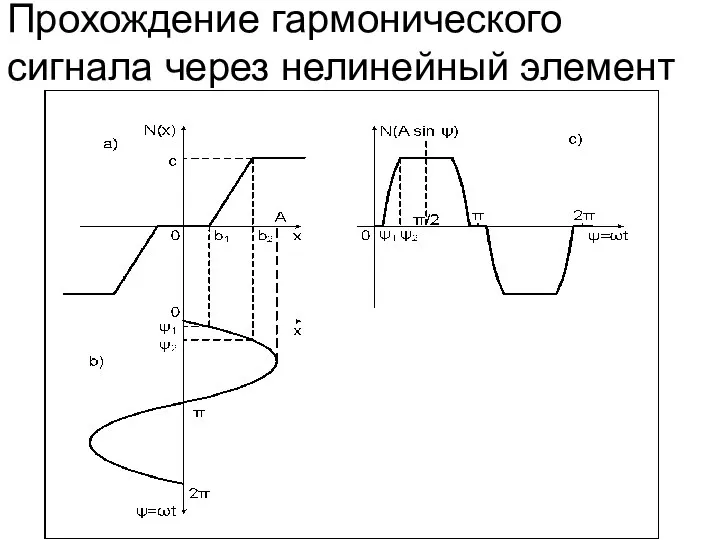
Фильтр высоких частот
На вход НЭ (N) подается гармонический сигнал с частотой ω.
x(t)=A sin(ωt) На его выходе устанавливаются колебания, не гармонической формы (например, прямоугольная волна).
u(t)=N(Asin(Ω t)) - периодическая функция с периодом Т= 2 π / Ω,
представим ее рядом Фурье в виде суммы гармоник с частотами
Ω, 2Ω, 3Ω, ... , они поступают на вход ЛЧ и, проходя через нее,
изменяет свою амплитуду в Ал(kω) раз,
где: Ал (ω) – АЧХ линейной части.
Гипотеза фильтра высокой частоты
выполняется, если АЧХ линейной
части удовлетворяет условию
Ал(2 Ω) < 0,05Ал(Ω) ,
т.е. АЧХ должна быть вида,
представленного на рисунке:
Такая АЧХ называется характеристикой типа фильтра.
Система с такой характеристикой не пропускает высокие частоты,
поэтому выходной сигнал ЛЧ будет практически содержать лишь
первую гармонику с частотой АК ωа =Ω.

Прохождение гармонического сигнала через нелинейный элемент

Метод гармонической линеаризации
Идея принадлежит Н.М. Крылову и Н.Н. Боголюбову и базируется на замене НЭ - линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на
выходе НЭ и эквивалентного ему линейного звена. Метод используется, если линейная часть системы удовлетворяет условиям «гипотезы фильтра»: отфильтровываются все возникающие на выходе НЭ гармонические составляющие, кроме первой гармоники.

Разложение периодического сигнала в ряд
Фурье
Выходной сигнал НЭ
Все гармоники, начиная со второй имеют достаточно малую амплитуду по сравне-нию с первой гармоникой и ими можно пренебречь.
Тогда уравнение вынужденных колебаний на выходе запишется в виде
где:
При а0=0:
Вывод: на вход подали гармонический сигнал и на выходе получили также гармонический. Следовательно, в рассмотрение можно ввести частотные характеристики, аналогичные характеристикам линейной системы.

Коэффициенты гармонической линеаризации
x(t)=A sin(ωt) – входной сигнал, → sin(ωt) = x/ A;
производная входного сигнала в операторной форме (p = d/dt):
px = Аωcos(ωt), → cos(ωt) = px / Аω.
Первая гармоника периодических колебаний на выходе НЭ:
Yн1= a1 sin(ωt) + b1 cos(ωt) = a1 x/ A+ b1 px / Аω =
= (q + q′ р/ ω) x;
Это уравнение гармонической линеаризации, где: q = a1/A; q′ = b1/A,
q и q′ - коэффициенты гармонической линеаризации, для различных нелинейных характеристик они приведены в справочниках по ТАУ.
В общем случае q(А, ω) и q′(А, ω) зависят от амплитуды А и частоты ω колебаний на входе НЭ,
для статических нелинейностей q(А) и q′(А) являются функцией только амплитуды А входного сигнала,
для статических однозначных нелинейностей q′(А) = 0.

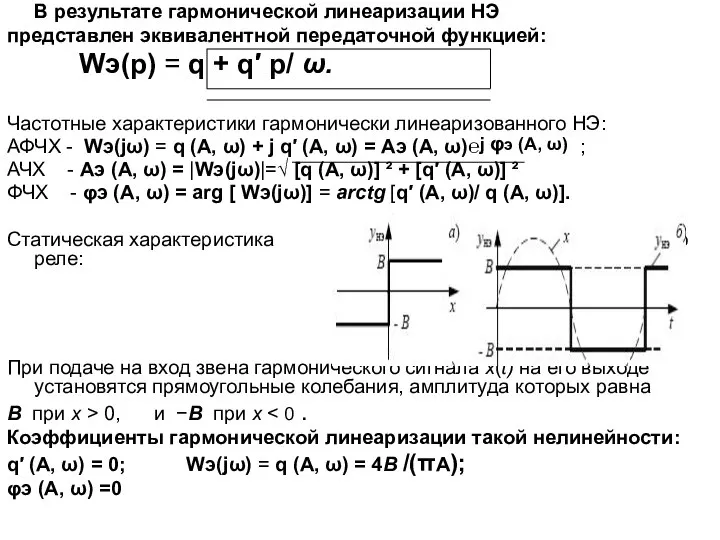
В результате гармонической линеаризации НЭ
представлен эквивалентной передаточной функцией:
Wэ(p) = q + q′ р/ ω.
Частотные характеристики гармонически линеаризованного НЭ:
АФЧХ - Wэ(jω) = q (А, ω) + j q′ (А, ω) = Аэ (А, ω)℮ ;
АЧХ - Аэ (А, ω) = |Wэ(jω)|=√ [q (А, ω)] ² + [q′ (А, ω)] ²
ФЧХ - φэ (А, ω) = arg [ Wэ(jω)] = arctg [q′ (А, ω)/ q (А, ω)].
Статическая характеристика двухпозиционного реле:
При подаче на вход звена гармонического сигнала x(t) на его выходе установятся прямоугольные колебания, амплитуда которых равна
B при x > 0, и −B при x < 0 .
Коэффициенты гармонической линеаризации такой нелинейности:
q′ (А, ω) = 0; Wэ(jω) = q (А, ω) = 4B /(πА);
φэ (А, ω) =0
j φэ (А, ω)

Уравнение гармонического баланса
Из структурной схемы АСУ
очевидно соотношение: x = - y,
для гармонического сигнала комплексное обозначение
x(t)=A sin(ωt) = А ℮.
По схеме:
y = Wэ(А) Wл(jω)* x = А ℮ * Wэ(А) Wл(jω) = - А ℮ .
Сократим на неравный нулю множитель А℮ и получим:
Wэ(А, ω) Wл(jω) = - 1 Это уравнение гармонического баланса.
- 1 = ℮,
где: φ (ω) = -(2k+1) π , при k =0,1,2,….
Если удастся найти действительные числа А = Аа и ω = Ω, которые обращают это уравнение в тождество, то в системе имеют место автоколебания почти гармонической формы с частотой Ω и амплитудой А.
j φ (ω)
j φ (ω)
j φ (ω)
j φ (ω)
j φ (ω)

При исследовании нелинейных систем по частотным характеристикам уравнение гармонического баланса записывают отдельно для модуля и аргумента эквивалентной комплексной передаточной
функции разомкнутой нелинейной системы:
│Wэ(А,jω)│*│Wл(jω)│= 1;
arg [Wэ(А,jω)Wл(jω)] = -(2k+1) π , при k =0,1,2,….
либо:
Аэ(А, ω) * Ал(ω) =1;
φэ(А,ω) + φл(ω) = -(2k+1) π , при k =0,1,2,….

Определение параметров АК - (Аа, Ω)
1 этап: Выполнить гармоническую линеаризацию НЭ -
Wэ(p) = q + q′ *р/ ω.
Запишем передаточную функцию
разомкнутой линеаризованной АСУ:
Wр(р) = Wл(р) Wэ(p) =
= Rл(р) * [q + q′ *р/ ω] /Qл (р).

2 этап: Для оценки возможности возникновения АК в линеаризованной нелинейной АСУ найдем
условия границы устойчивости.
Также, как и при анализе устойчивости
линейных систем АК существуют, если при
А = Аа и ω = Ω,
характеристическое уравнение линеаризованной системы
Qл(p) + Rл(p)×[q(А,ω) + q′(А,ω)* р/ω] = 0
имеет пару мнимых корней pi = j Ω и
pi+1 = − j Ω.

3 этап: исследовать устойчивость АК
АК устойчивы, если их амплитуда А = Аа, частота ω = Ω и форма устойчивы к малым возмущениям начальных условий.
Для этого необходимо выполнить условие:
∂X(A,ω) ∂Y(A, ω) ∂Y(A, ω) ∂ X(A, ω)
∂A ∂ ω А=Аа ∂A ∂ ω А=Аа > 0 ω = Ω ω = Ω
Условие является лишь необходимым, то есть позволяет отсеять заведомо неустойчивые АК.

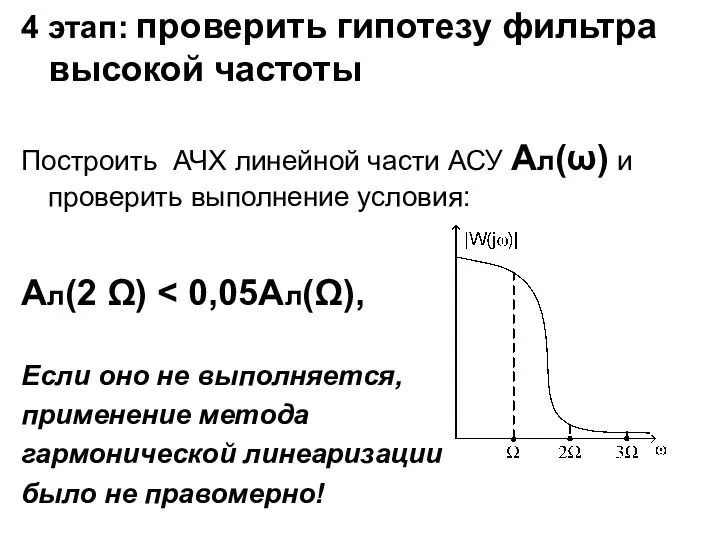
4 этап: проверить гипотезу фильтра высокой частоты
Построить АЧХ линейной части АСУ Ал(ω) и проверить выполнение условия:
Ал(2 Ω) < 0,05Ал(Ω),
Если оно не выполняется,
применение метода
гармонической линеаризации
было не правомерно!

ПО КРИТЕРИЮ МИХАЙЛОВА
АСУ находится на границе устойчивости, если годограф Михайлова D(jω) проходит через начало координат, т.е.:
D(jω)=Qл(jω)+Rл(jω)*[q(А,ω)+ j* q′(А,ω)]=
=X(А,ω) + jY(А,ω)= 0.
параметры АК рассчитываются из системы уравнений:
(*) X(А,ω) = 0; А = Аа
Y(А,ω) = 0. ω = Ω
Из (*) можно найти зависимость А и Ω АК от параметров АСУ, например, от коэффициента передачи k линейной части. Для чего в (*) k считают переменной величиной и записывают в виде: X(А,ω,k) = 0;
Y(А,ω,k) = 0.
По графикам A = f(k), Ω = f(k) можно выбрать такой k, при котором А и Ω возможных АК имеют допустимые значения, или они вообще отсутствуют.
j
Re

Частотный метод (Л.С.Гольдфарб)
По критерию Найквиста незатухающие колебания (АК) в гармонически линеаризованной нелинейной АСУ возникают, если АФЧХ разомкнутой АСУ проходит через точку [−1, j0]:
Wр(jω,А) = Wл(jω) Wэ(jω,А) = −1. (*)
В случае статической характеристики НЭ условие (*) принимает вид: Wл(jω) =-1/ Wэ(jω,А)
Решение этого уравнения относительно Ω и Аа можно получить графически как точку пересечения АФЧХ - Wл(jω) и годографа обратной АФЧХ нелинейной части -1/ Wэ(jω,А) , взятой с обратным знаком. Если эти годографы не пересекаются,
то режим АК в АСУ не существует.

Для устойчивости АК с частотой Ω и амплитудой Аa требуется, чтобы изображающая точка при перемещении по годографу нелинейной части
-1/ Wэ(jω,А) в направлении увеличения амплитуды Аa подходила к точке пересечения характеристик -1/ Wэ(jω,А)и Wл(jω) изнутри АФЧХ Wл(jω).
На рис. годографы
расположены так, что в
нелинейной АСУ существуют
устойчивые АК. Значение Аа
определяем на - 1/ Wэ(jω,А),
а Ω - на Wл(jω).

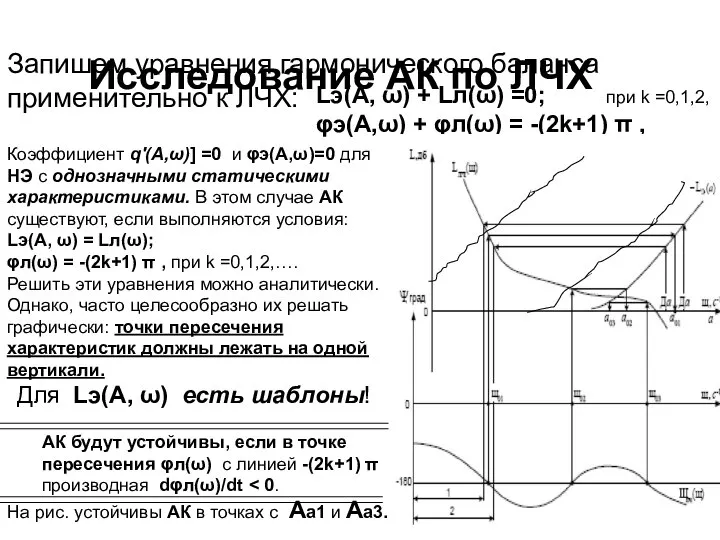
Исследование АК по ЛЧХ
Запишем уравнения гармонического баланса применительно к ЛЧХ:
Lэ(А, ω) + Lл(ω) =0; при k =0,1,2,
φэ(А,ω) + φл(ω) = -(2k+1) π ,
Коэффициент q′(А,ω)] =0 и φэ(А,ω)=0 для НЭ с однозначными статическими характеристиками. В этом случае АК существуют, если выполняются условия: Lэ(А, ω) = Lл(ω);
φл(ω) = -(2k+1) π , при k =0,1,2,….
Решить эти уравнения можно аналитически. Однако, часто целесообразно их решать графически: точки пересечения характеристик должны лежать на одной вертикали.
Для Lэ(А, ω) есть шаблоны!
АК будут устойчивы, если в точке
пересечения φл(ω) с линией -(2k+1) π
производная dφл(ω)/dt < 0.
На рис. устойчивы АК в точках с Аа1 и Аа3.

Тренировочное задание
Исследовать АК в нелинейной системе,
линейная часть которой имеет следующую передаточную функцию
Wл(р)=k/[p(T1p+1)(T2p+1)] , где k=200 c-1; T1=1.5 c; T2=0.015 c,
а в качестве НЭ используется реле с
зоной нечувствительности при с=10, b=2.
Р е ш е н и е. Из справочника для реле с зоной
нечувствительности находим коэффициенты
гармонической линеаризации: q′(А,ω)=0,
q(А,ω)=4с/ (π A)*√1-(b/A)² при A≥ b.
Ответ:Аа=58В; Ω=4,3рад/c.

Тренировочное задание
В соответствии с критерием Бендиксона в рассматриваемой области не существует замкнутых фазовых траекторий при выполнении определенных условий. Сформулируйте эти условия
Какая функция называется функцией последования?
Каким образом в соответствии с методом преобразования можно определить в системе существующий режим?

Тренировочное задание
Какими свойствами должна обладать линейная часть нелинейной системы, чтобы можно было применить к исследованию режима автоколебаний метод гармонического баланса?
Какой факт лежит в основе доказательства существования в нелинейной системе автоколебаний?
Сформулируйте аналог критерия Найквиста для исследования устойчивости автоколебаний.

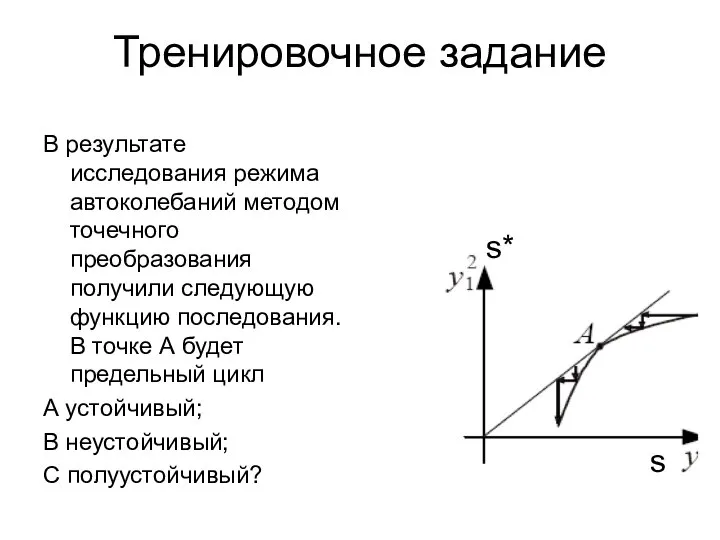
Тренировочное задание
В результате исследования режима автоколебаний методом точечного преобразования получили следующую функцию последования. В точке А будет предельный цикл
А устойчивый;
В неустойчивый;
С полуустойчивый?
s*
s

Тренировочное задание
В результате построения функции последования получим s* > s , что свидетельствует о том, что в системе будет процесс
А -колебательный;
В -расходящийся;
С -затухающий.

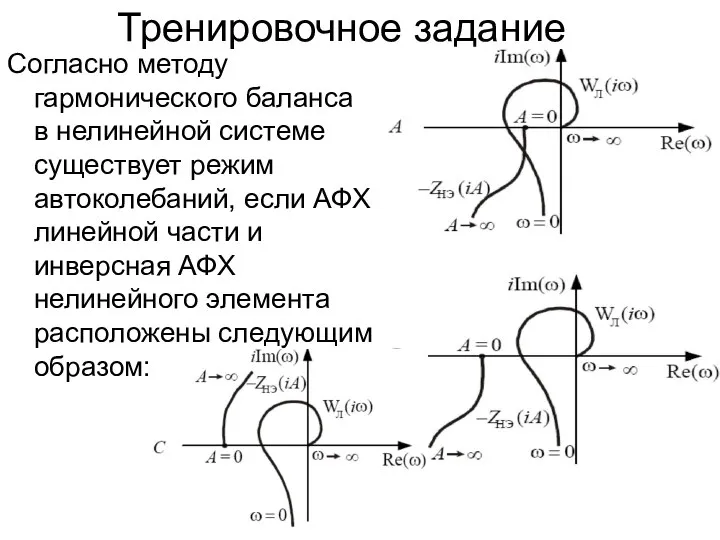
Тренировочное задание
Согласно методу гармонического баланса в нелинейной системе существует режим автоколебаний, если АФХ линейной части и инверсная АФХ нелинейного элемента расположены следующим образом:

Тренировочное задание
Основное уравнение, используемое в методе гармонического баланса, имеет вид