Содержание
- 2. Иллюстрация механических колебаний на примере маятника Фуко После просмотра телепередачи о архитектурных достопримечательностях Санкт – Петербурга
- 3. Вначале опыт был выполнен в узком кругу, но так заинтересовал Наполеона III, французского императора, что он
- 4. Эксперимент 1 Проделаем следующий опыт. Привяжем к карандашу нитку с небольшим грузиком. Положив на стол линейку
- 5. Эксперимент 2 А теперь я предлагаю сделать другую модель маятника Фуко. Перевернём вверх ногами табуретку и
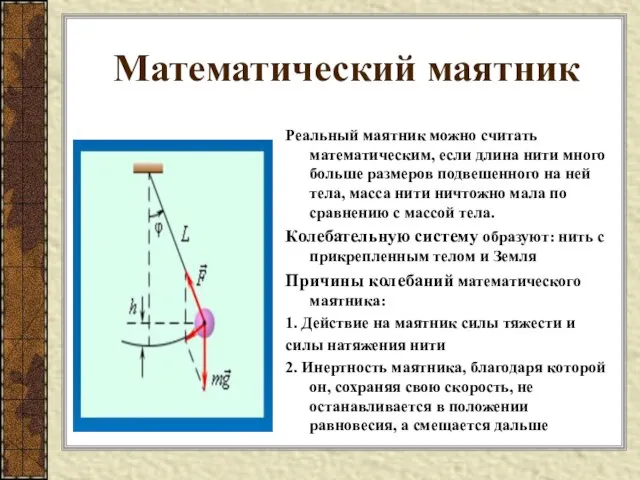
- 6. Математический маятник Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней
- 7. Галилео Галилей (1564-1642) Великий итальянский ученый – один из создателей точного естествознания. Родился в городе Пизе,
- 8. Сохранилось предание о том, как молодой студент медицинского факультета Галилео Галилей в одно из воскресений 1583
- 9. Период колебания математического маятника прямо пропорционален длине маятника и обратно пропорционален ускорению свободного падения. Общий вывод:
- 10. Компьютерная модель математического маятника, созданная с использованием программы Macromedia Flash 5.
- 11. Гюйгенс Христиан (1629 – 1695) Формула периода колебаний математического маятника впервые была получена на опыте голландским
- 12. В 1656 году в возрасте 27 лет Гюйгенсом были сконструированы первые маятниковые часы со спусковым механизмом.
- 13. А как выяснить зависимость периода колебания от ускорения свободного падения? Можно искусственно увеличить тяготение к Земле,
- 14. Практическое использование колебаний маятника Ускорение свободного падения меняется с географической широтой, так как плотность земной коры
- 15. Это интересно… О маятнике, его роли и влиянии на жизнь и судьбу человека, писали многие философы
- 17. Скачать презентацию












 Пространственная дискретизация
Пространственная дискретизация Школы – лидеры
Школы – лидеры О проекте > Статистика > Аудитория > Рекламные возможности > Наши рекламодатели > Контакты
О проекте > Статистика > Аудитория > Рекламные возможности > Наши рекламодатели > Контакты Лекция 1 (1)
Лекция 1 (1) Styie.ua Магазин одежды
Styie.ua Магазин одежды Классификация методов и технологий обучения в ВУЗе
Классификация методов и технологий обучения в ВУЗе Игровой судебный процесс по делу об активном избирательном праве осужденных
Игровой судебный процесс по делу об активном избирательном праве осужденных Производство беспроводных GSM систем безопасности, контроля и мониторинга Беспроводные GSM контрольные охранные панели GSM системы к
Производство беспроводных GSM систем безопасности, контроля и мониторинга Беспроводные GSM контрольные охранные панели GSM системы к Объектная ориентация Java
Объектная ориентация Java  Комитет по взаимодействию с миноритарными акционерами Сбербанка России
Комитет по взаимодействию с миноритарными акционерами Сбербанка России Ваш профессиональный маршрут
Ваш профессиональный маршрут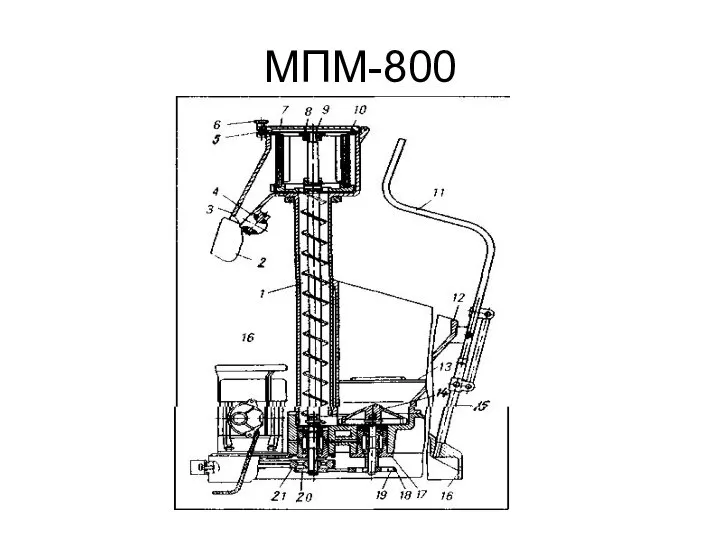 Машины для теста
Машины для теста СПАСИ СЕБЯ САМ
СПАСИ СЕБЯ САМ Объект политологии
Объект политологии РВАТЬ ЗУБЫ И МЫТЬ ДЕНЬГИ: ОБ ОДНОМ ТИПЕ УПОТРЕБЛЕНИЯ ПРОСТЫХ ИМПЕРФЕКТИВОВ В РУССКОМ ЯЗЫКЕ Анна А.Зализняк Институт языкознания Р
РВАТЬ ЗУБЫ И МЫТЬ ДЕНЬГИ: ОБ ОДНОМ ТИПЕ УПОТРЕБЛЕНИЯ ПРОСТЫХ ИМПЕРФЕКТИВОВ В РУССКОМ ЯЗЫКЕ Анна А.Зализняк Институт языкознания Р Графика как вид изобразительного искусства
Графика как вид изобразительного искусства Визитная карточка группы «Почемучки» МДОУ д/с№75 общеразвивающего типа
Визитная карточка группы «Почемучки» МДОУ д/с№75 общеразвивающего типа Технология приготовления и оформления блюда из тушеной рыбы
Технология приготовления и оформления блюда из тушеной рыбы Презентация на тему Холера
Презентация на тему Холера 2b8483313b22fe88
2b8483313b22fe88 Prevention of Child Disability: NGO contribution to the interdisciplinary approach in health and social careПрофилактика детской инвалидности: вклад неправительственной организ
Prevention of Child Disability: NGO contribution to the interdisciplinary approach in health and social careПрофилактика детской инвалидности: вклад неправительственной организ Think Backwards
Think Backwards Развитие межкультурной компетенции и межкультурной коммуникации молодежи в русско-немецком языковом пространстве
Развитие межкультурной компетенции и межкультурной коммуникации молодежи в русско-немецком языковом пространстве Заповедник "Богдинско-Баскунчакский"
Заповедник "Богдинско-Баскунчакский"  Сухие смеси и отделочные п.ф. промышленного производства
Сухие смеси и отделочные п.ф. промышленного производства Неформальная занятость: к портрету "известной незнакомки"
Неформальная занятость: к портрету "известной незнакомки" Работа ученика 3 «А»класса Работа ученика 3 «А»класса Речистова Димы.
Работа ученика 3 «А»класса Работа ученика 3 «А»класса Речистова Димы. Презентация на тему Комфорт обучающихся на занятиях в кружках
Презентация на тему Комфорт обучающихся на занятиях в кружках