Большие дополнительные пространственные измерения: многомерная теория поля и гравитация на масштабе ТэВ

Проблема иерархий: два масштаба в теории
Впервые сформулирована С.Вайнбергом ’76
Радиационные поправки к
«голой» массе хиггса
очень большие вклады
должны быть скомпенсир.
подходящим выбором m0:
Добавка от калибровочного сектора:
Насколько большим м.б. UV масштаб Λ ? Два стандартных UV обрезания
Абсолютно непонятно, как обеспечить тонкую настройку
с такой колоссальной точностью !
(QED:
)

Несколько слов о естественности: уроки QCD
ΛQCD ~ 100 MeV MPl ~ 1019 GeV
Естественный механизм генерации этой гигантской иерархии масштабов
Метод ренормгруппы : логарифмический бег константы связи:
: Асимптотическая свобода +
размерная трансмутация
Естественное динамическое происхождение иерархии безо всякой тонкой
подгонки параметров: «сильная» естественность теории
Параметр физической теории, раз выбранный малым, остается таковым, вследствие
специального (мультипликативного) вклада от радпоправок:
«техническая» естественность
Симметрия позволяет сохранить малое значение параметра (защищающая сим.)
Теория с фазовым переходом: нарушение киральной симетрии,
,
конденсаты определяют значения масс в спектрах мезонов и барионов
Пример: QED, me =0 защищающая киральная симметрия U(1)L x U(1)R

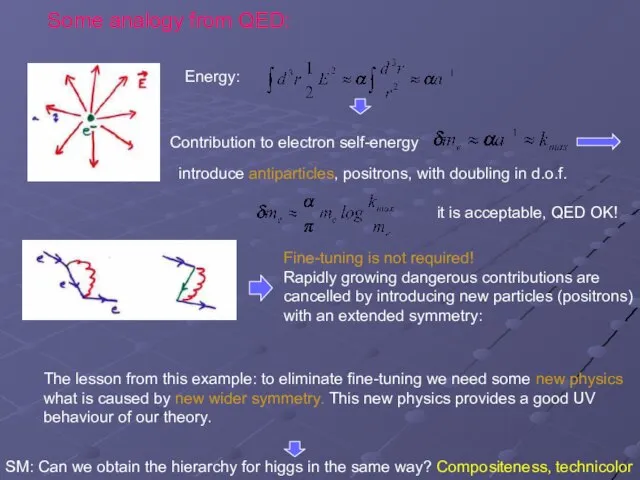
Some analogy from QED:
Fine-tuning is not required!
Rapidly growing dangerous contributions are
cancelled by introducing new particles (positrons)
with an extended symmetry:
The lesson from this example: to eliminate fine-tuning we need some new physics
what is caused by new wider symmetry. This new physics provides a good UV
behaviour of our theory.
Energy:
Contribution to electron self-energy
introduce antiparticles, positrons, with doubling in d.o.f.
it is acceptable, QED OK!
SM: Can we obtain the hierarchy for higgs in the same way? Compositeness, technicolor

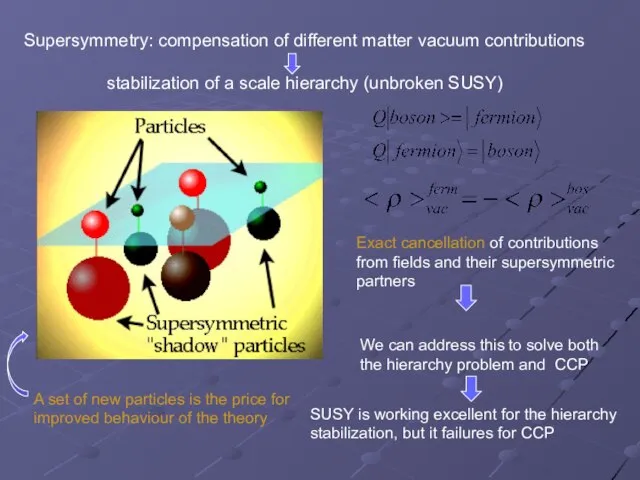
Supersymmetry: compensation of different matter vacuum contributions
stabilization of a scale hierarchy (unbroken SUSY)
Exact cancellation of contributions
from fields and their supersymmetric
partners
We can address this to solve both
the hierarchy problem and CCP
SUSY is working excellent for the hierarchy stabilization, but it failures for CCP
A set of new particles is the price for
improved behaviour of the theory

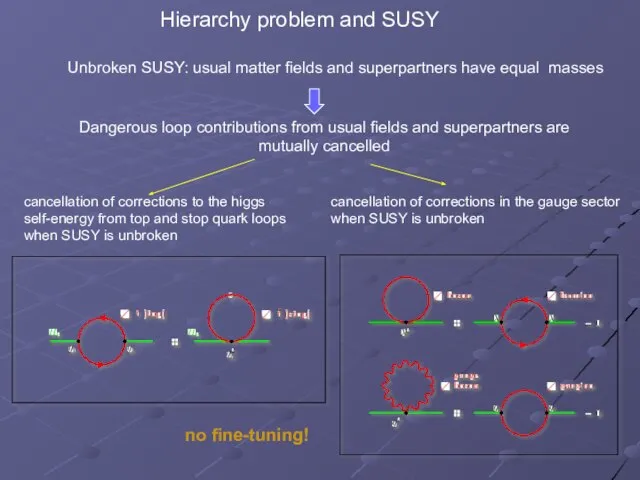
Hierarchy problem and SUSY
cancellation of corrections to the higgs
self-energy from top and stop quark loops
when SUSY is unbroken
cancellation of corrections in the gauge sector
when SUSY is unbroken
Unbroken SUSY: usual matter fields and superpartners have equal masses
Dangerous loop contributions from usual fields and superpartners are
mutually cancelled
no fine-tuning!

If this relation are satisfied fine-tuning is not required!!
Hierarchy problem and SUSY
Important condition: masses of superpartners can not be much
larger then 1 TeV!!!
Superpartner contributions modify the behaviour of running coupling constants:
Unification of running coupling constants, MSUSY ≈ 1 TeV
IF SUSY is broken at the scale about 1 TeV:
A difference between values of masses of usual
fields and superpartners is about Δm

Защищающая киральная симметрия
Иерархия масштабов может сохраняться естественным образом
(в «техническом» смысле, т.е. быть стабилизированной, а также и в сильном
смысле - динамически), если теория обладает некоторой защищающей
симметрией, которая запрещает возникновения радпоправок, будучи
ненарушенной, и обеспечивает малость поправок в случае нарушения симметрии
(вклад от поправок будет порядка величины нарушения симметрии).
Один хороший пример - SUSY. Защищающая симметрия в этом случае -
киральная симметрия для частиц и их суперпартнеров, поскольку они
располагаются в одном и том же супермультиплете. Для ненарушенной SUSY
эта симметрия - точная, и любые радпоправки запрещены. Для нарушенной на
некотором энергетическом масштабе SUSY величина вклада от радпоправок
конечна, и порядка масштаба нарушения
Существуют и другие примеры естественных теорий, в частности, хорошо
известные модели техницвета – «копирование» КХД для более высоких
энергий. Защищающая симметрия и в этом случае – киральная.
Сильновзаимодействующий сектор – SSB на некотором масштабе
(порядка нескольких ТэВ).
Нет других «естественных» механизмов SSB в 4D !

Resume on 4D theories with SSB
The hierarchy of scales in SM is not “a technical” but a principal problem, a weak point of the model that must be solved to get a blameless scheme.
SUSY:
SUSY prevents the hierarchy against HO contributions which destroy it
it solves the problem of hierarchy stabilization and eliminates the necessity
of fine-tuning.
SUSY scale appears to be equal 1 TeV (low-scale SUSY) as motivated by running coupling constant unification. B,L conservation
SUSY does not solve the hierarchy problem in whole as it does not explain the hierarchy itself, that is where two energy scale in theory are going from (It is insufficient to stabilize the hierarchy to explain the hierarchy!)
Strong coupled sector:
Composite higgs model (or Technicolor): Λ ~ 5-10 TeV or higher, large
contribution to EW observables - ruled out by EW precision data
Hard to obtain quantitative predictions because of strong coupling regime corrections for technifermions and technibosons - confinement!
Interesting intersections with new ideas of multidimensional gravity through AdS/CFT correspondence!

Alternative new physics beyond the TeV scale
Composite higgs model (or Technicolor): 70’s of last century
Λ ~ 3-5 TeV or higher
hard to obtain quantitative predictions because of strong coupling regime corrections for technifermions and technibosons - again the problem of
confinement!
interesting intersections with new ideas of multidimensional gravity through AdS/CFT correspondence!
Large extra spatial dimensions: last decade
Planck scale is an effective scale regularized by a size of extra dimensions.
flat bulk space curve bulk space
ADD-type, power hierarchy RS-type, exponential hierarchy
negative CC, inflation
Little higgs and little hierarchy (N.Arkani-Hamed, E.Cohen, E.Katz...): 2001
All of this is along the direction of naturalness philosophy

Геометрия многомерного объема:
иерархии без симметрий

Стандартный калуца-кляйновский подход
(4+1)D-теория свободного скалярного поля. Одно компактное дополнительное пространственное измерение с условием периодичности по доп. коорд.:
КК-декомпозиция:
угловой момент
массы КК-мод
Существует однородная нулевая мода с m=0, распространяющаяся вдоль браны
(модуль). 4D-лоренц-инвариантность не нарушена, трансляционная инв-ть
нарушена в направлении, перпендикулярном бране
mKK не ниже ТэВ (из эксперимента)
Несколько ED:
по-прежнему одна
нулевая мода, но
много КК-мод с фиксир.
массой

5D vs эффективное 4D-описание
Действие 5D-скалярного поля:
КК-декомпозиция:
объем ED
Свободное действие для бесконечного набора 4D скалярных полей
Каноническая нормировка позволяет привести действие к совершенно
стандартному виду

Взаимодействующее поле
Отрицательная степень массы для к-ты связи – неперенормируемая теория
Фундаментальный масштаб – значение энергии, при
которой теория переходит в режим сильной связи, и
эффективное описание становится неприменимым
Как связаны многомерная и 4D константы взаимодействия? (КК-декомпозиция,
учет только нулевой моды)
4D константа связи – не фундаментальная, а эффективная, выведенная из
многомерной
нормировка
два параметра:
R и M(5)

парное рождение КК-мод,
сохранение углового момента
(не верно для BW ! )
Некоторые очевидные следствия:
1. Условие для слабосвязанной теории
2. Условие на массы КК-мод
Размер ED должен существенно превышать значение обратной фундам. массы!
легкие первые КК-моды
3. Взаимодействие нулевой моды и высших возбуждений
единственная безразмерная к-та связи

Мир на бране – локализация полей на 3D-гиперповерхности. Как сделать?
ТС – свои методы
КТП – локализация на топологическом дефекте
(Рубаков, Шапошников, 1983)
E.o.M.
Существует топологически нетривиальное решение –
доменная стенка (кинк), зависящее только от
дополнительной координаты - одномерное
Нарушает трансляционную инвариантность вдоль y
Классические IR вакуумы теории
(космологическая константа)
Потенциал «подходящего вида»,
EDs могут быть развернуты
(бесконечные)

Флуктуации скалярного поля над этим классическим решением:
Линеаризованные E.o.M.
потенциальная стенка
4D-масса
КК-декомпозиция:
Нулевая мода, m=0
Нулевая 4D-мода локализована на бране.

дискретный спектр, отделенный от нулевой моды щелью,
моды все еще группируются вблизи браны, и подавлены
степенным образом вдали от нее
непрерывный спектр мод, нелокализованных
вблизи браны, и уходящих вдоль дополнительного
Измерения на бесконечность:
При энергиях выше фундаментального
масштаба частицы могут уходить в
дополнительные измерения:
сигналы с недостающей энергией
- пороговые эффекты e+e- Emis
явное несохранение энергии в процессах
взаимодействий (e+e- γ + Emis)
Высшие КК-моды

Локализация фермионов на дефекте
E.o.M.
Нулевая мода с m=0
Существует единственное решение
нормируемая мода

Спектр фермионных мод
Нулевая мода получилась локализованной и
Киральной (теорема об индексе)
Чтобы получить несколько нулевых мод (3 поколения частиц СМ), надо
увеличить число дополнительных измерений, и рассмотреть
топологические дефекты высших размерностей:
N=2 – ANO вихрь
N=3 – монополь ‘т Хофта-Полякова
Количество локализованных нулевых мод равно топологическому
числу дефекта

Что насчет калибровочного поля?
Проблема, связанная с требованием зарядовой универсальности для
взаимодействия разных заряженных полей материи с калибровочными
бозонами
Пусть есть нулевая мода калибровочного бозона A0(y). Тогда взаимодействие
с заряженными полями определяется интегралом от перекрытия функций
профилей нулевых мод фермионов:
Зависит от формы функций профилей – зарядовая неуниверсальность,
разные выражения для разных нулевых мод. Очень плохо !
Как можно решить проблему?
Все нулевые фермионные моды имеют одинаковую форму – верно для
модели с некоммутативнами солитонами (Рубаков)
A0 = Const – не зависит от y. несохранение заряда!
Вообще нет калибровочных полей в многомерном объеме – конфайнмент

Пример: юкавская иерархия масс фермионов,
смешивание поколений etc.
Три нулевые фермионные моды, локализованные на одном топологическом дефекте (6D-теория, космологическая струна), имеющие разные профили:
1 поколение
2 поколение
3 поколение
Приблизительная симметрия вращений в перпендикулярных к бране
направлениях (в доп. измерениях) обеспечивает малое смешивание между
поколениями
2. Разные массы фермионов обеспечиваются разной радиальной формой
профилей нулевых мод и разным перекрытием WF фермионов и
хиггсовской нулевой моды, локализованной на дефекте
3. Слабые взаимодействия, несохраняющие лептонное и барионное число
КК-моды W,Z – сохр. угл. мом.

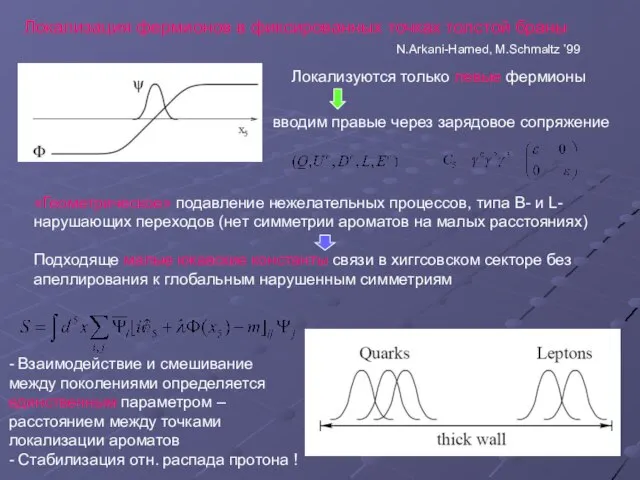
«Геометрическое» подавление нежелательных процессов, типа B- и L-нарушающих переходов (нет симметрии ароматов на малых расстояниях)
Подходяще малые юкавские константы связи в хиггсовском секторе без апеллирования к глобальным нарушенным симметриям
Локализация фермионов в фиксированных точках толстой браны
- Взаимодействие и смешивание
между поколениями определяется
единственным параметром –
расстоянием между точками
локализации ароматов
- Стабилизация отн. распада протона !
N.Arkani-Hamed, M.Schmaltz ’99
Локализуются только левые фермионы
вводим правые через зарядовое сопряжение