Содержание
- 2. Цели: изучить быстрый счёт с использованием нестандартных приёмов устного счёта, познакомить с упрощёнными приёмами устных вычислений,
- 3. Наша с вами встреча посвящена изучению способов быстрого счёта, в частности, быстрому умножению. Эти вопросы издревле
- 4. ФИЛЬМ
- 5. 1. Умножение числа на 11 8 Следует «раздвинуть» цифры числа, умножаемого на 11, и в образовавшийся
- 7. 2. Умножение чисел на 111, 1111 и т.д. Чтобы двузначное число умножить на 111, 1111 и
- 8. Реши сам: физкультминутка
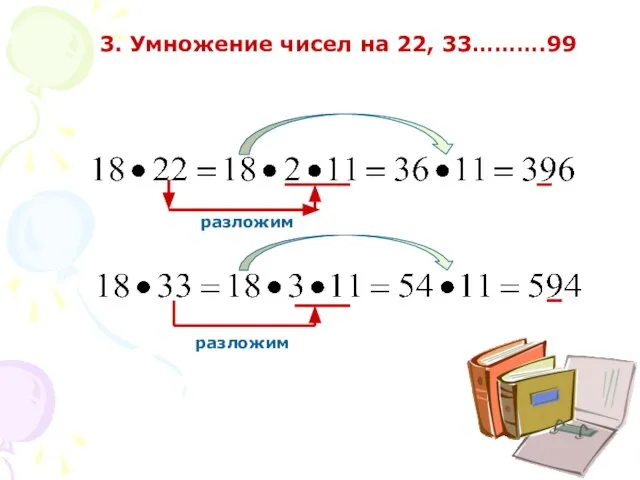
- 10. 3. Умножение чисел на 22, 33……….99 разложим разложим
- 11. РЕШИ САМ:
- 12. 4.Возведение в квадрат двузначных чисел, оканчивающихся на 5: 1=9 и в конце всегда приписываем 25( т.к.5*5=25)
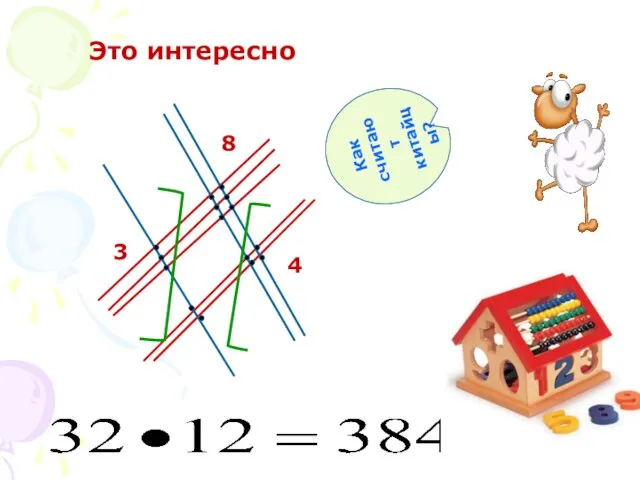
- 13. 8 3 4 Это интересно Как считают китайцы?
- 14. Сегодня мы еще раз убедились в том, что в самом обыкновенном устном счете, как и во
- 15. Синквейн – это один из приемов активизации познавательной активности учащихся на уроке. Слово «синквейн» происходит от
- 16. 1. Экзамен. 2. Строгий, трудный. 3. Проверяет, доказывает, подтверждает 4. Что ты знаешь, а чего не
- 18. Скачать презентацию




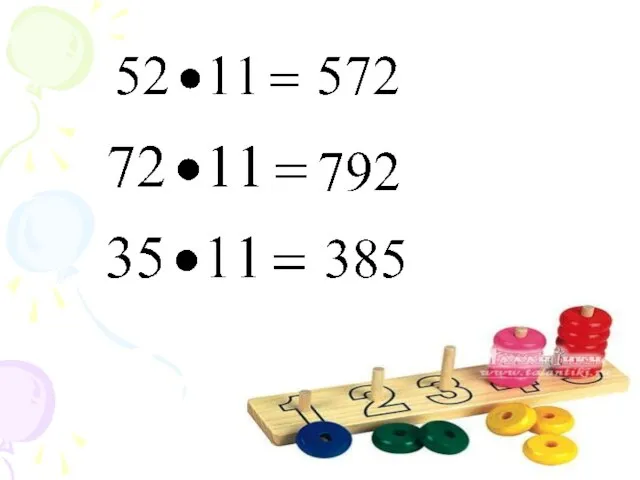








 The geography of the USA
The geography of the USA  20140604_antarktida
20140604_antarktida EVENT-АЛЬБОМ
EVENT-АЛЬБОМ Творческий проект Лопатка кухонная
Творческий проект Лопатка кухонная Коварные Е
Коварные Е Huawei P30 lite vs Samsung А50
Huawei P30 lite vs Samsung А50 Презентация на тему Во времена Древней Руси
Презентация на тему Во времена Древней Руси  Request Reply The main aims of the writing
Request Reply The main aims of the writing Роль физической культуры и спорта в нашей жизни
Роль физической культуры и спорта в нашей жизни Влияние электромагнитного излучения на здоровье человека
Влияние электромагнитного излучения на здоровье человека Первое родительское собрание
Первое родительское собрание Автосцепка
Автосцепка «Теория и методика музыкального развития с практикумом»
«Теория и методика музыкального развития с практикумом» Технология педагогического общения
Технология педагогического общения Христианская церковь в раннее средневековье
Христианская церковь в раннее средневековье Бесплатный курс АвтоПраво
Бесплатный курс АвтоПраво 2b
2b Тепловые насосы BROS
Тепловые насосы BROS Участие центров правовой информации библиотек в профилактике наркомании и пропаганде здорового образа жизни
Участие центров правовой информации библиотек в профилактике наркомании и пропаганде здорового образа жизни Кто его раздевает, тот слёзы проливает
Кто его раздевает, тот слёзы проливает Эковожатый. Социальная сфера
Эковожатый. Социальная сфера Рациональное пользование полезных ископаемых Пермского края
Рациональное пользование полезных ископаемых Пермского края 571 В вышине под небесами
571 В вышине под небесами Какие бывают финансовые риски
Какие бывают финансовые риски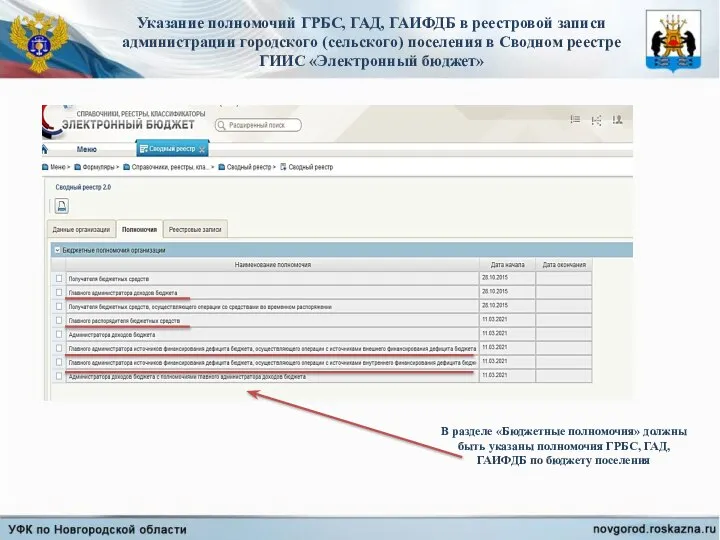 Полномочия ГРБС, ГАД, ГАИФДБ
Полномочия ГРБС, ГАД, ГАИФДБ Исполнение комплексного плана Совета ТОС «Правые Чемы» в 2011 году
Исполнение комплексного плана Совета ТОС «Правые Чемы» в 2011 году Пенопласт
Пенопласт Гуманитарная методология: прочтение, программа, профанация?
Гуманитарная методология: прочтение, программа, профанация?