Центральная симметрия

Центральная симметрия
Что такое центральная симметрия Что такое центральная симметрия ?
Доказательство центральной симметрии
О симметрии фигур
Центральная симметрия на графиках
Применение центральной симметрии в жизни

Центральная симметрия
Определение центральной симметрии: поворот на угол 180 градусов называется центральной симметрией.
Еще можно дать такое определение
Центральная симметрия с центром в точке O это такое отображение плоскости, при котором любой точке X сопоставляется такая точка X', что точка O является серединой отрезка XX'.

Доказательство центральной симметрии
Проводим отрезки АА’ и ВВ’, они проходят через т.О
Измеряем и убеждаемся, что АС=AC’, АВ=АВ’,
Порядок построения точки, центрально симметричной точке В на бумаге:
1.Проводим луч ВА.
2.Откладываем на нем от т А в другую сторону отрезок АВ’

О симметрии фигур
Говорят, что фигура обладает симметрией (симметрична) , если существует такое движение (не тождественное), переводящее эту фигуру в себя. Например, фигура обладает поворотной симметрией , если она переходит в себя некоторым поворотом.
Рассмотрим симметрию некоторых фигур:
1. Отрезок имеет две оси симметрии (серединный перпендикуляр и прямая, содержащая этот отрезок) и центр симметрии (середина).
2. Треугольник общего вида не имеет осей или центров симметрии, он несимметричен. Равнобедренный (но не равносторонний) треугольник имеет одну ось симметрии: серединный перпендикуляр к основанию.
3. Равносторонний треугольник имеет три оси симметрии (серединные перпендикуляры к сторонам) и поворотную симметрию относительно центра с углом поворота 120 ° .
4.У любого правильного n-угольника есть n осей симметрии, все они проходят через его центр. Он также имеет поворотную симметрию относительно центра с углом поворота
При четном n одни оси симметрии проходят через противоположные вершины, другие - через середины противоположных сторон.
При нечетном n каждая ось проходит через вершину и середину противополжной стороны.
Центр правильного многоугольника с четным числом сторон является его центром симметрии. У правильного многоугольника с нечетным числом сторон центра симметрии нет.
Любая прямая, проходящая через центр окружности является ее осью симметрии, окружность также обладает поворотной симметрией, причем угол поворота может быть любым.

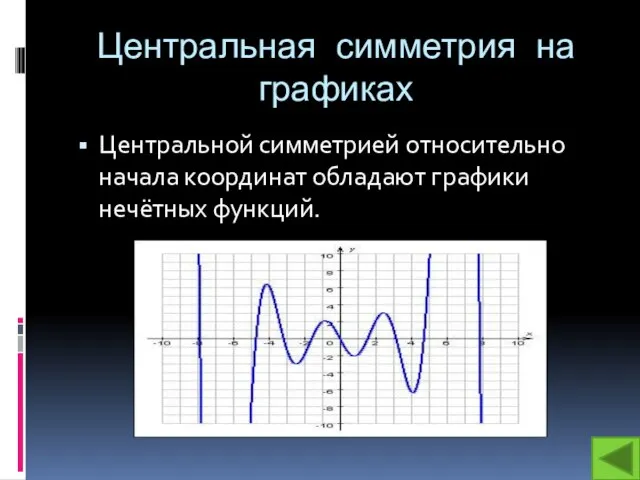
Центральная симметрия на графиках
Центральной симметрией относительно начала координат обладают графики нечётных функций.

Применение центральной симметрии в жизни
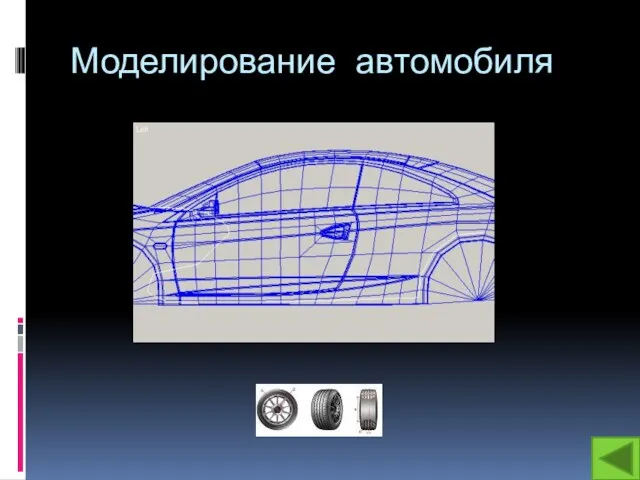
Центральная симметрия применяется во многих отраслях, например в моделировании автомобиляЦентральная симметрия применяется во многих отраслях, например в моделировании автомобиля , архитектуре , инструментах (сверло) , строй материалах (пружина) и т.д.

Моделирование автомобиля

Архитектура