ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

Содержание
Центральная симметрия
Задачи
Построение
Центральная симметрия в окружающем мире
Заключение

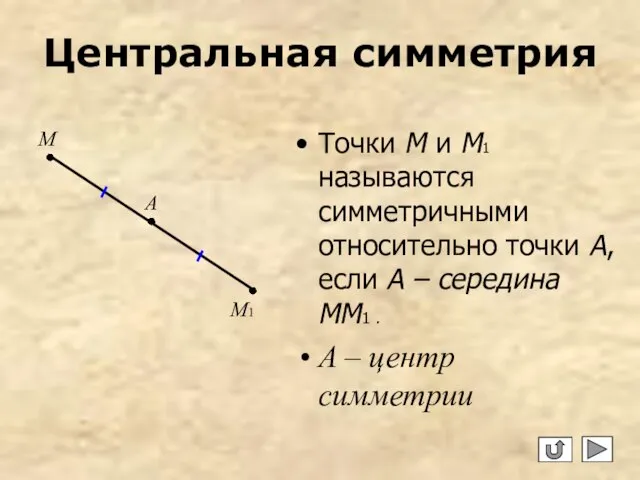
Центральная симметрия
Точки М и М1 называются симметричными относительно точки А, если A – середина MM1 .
A – центр симметрии
A
M
M1

Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

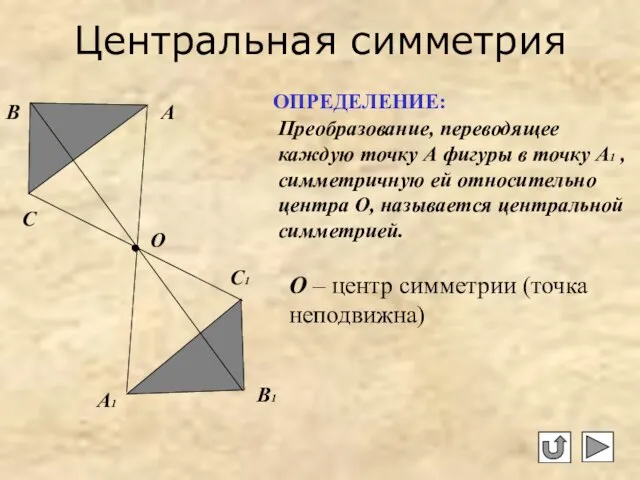
Центральная симметрия
Преобразование, переводящее каждую точку А фигуры в точку А1 , симметричную ей относительно центра О, называется центральной симметрией.
ОПРЕДЕЛЕНИЕ:
О
О – центр симметрии (точка неподвижна)
А
А1
B
B1
C
C1

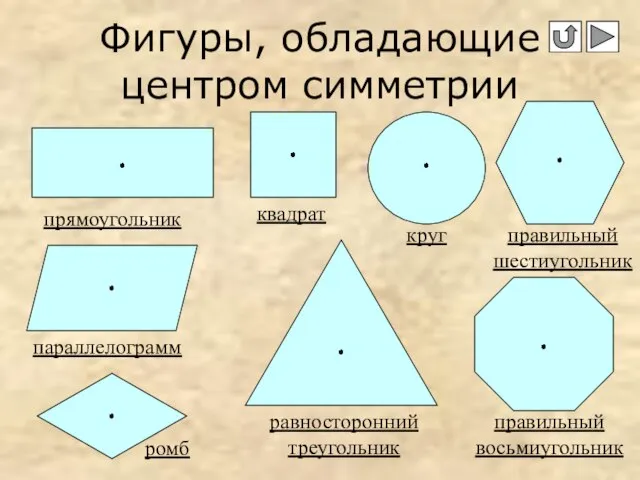
Фигуры, обладающие центром симметрии
прямоугольник
квадрат
круг
правильный шестиугольник
параллелограмм
ромб
равносторонний треугольник
правильный восьмиугольник

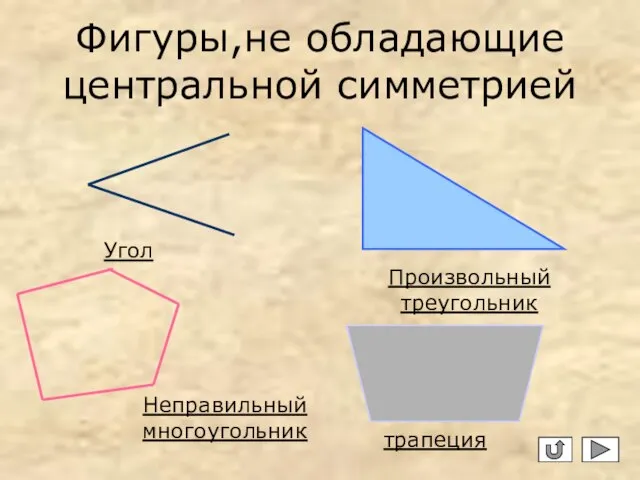
Фигуры,не обладающие центральной симметрией
Неправильный многоугольник
Произвольный треугольник
Угол
трапеция

Построение
точки, симметричной данной
отрезка, симметричного данному
треугольника, симметричного данному

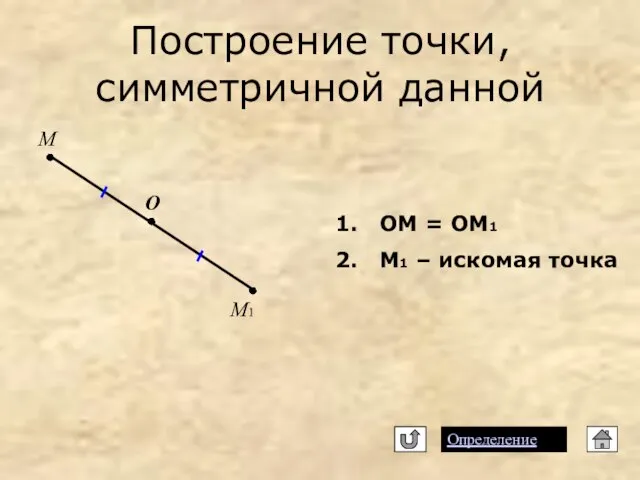
Построение точки, симметричной данной
Определение
ОМ = ОМ1
М1 – искомая точка
О
M
M1

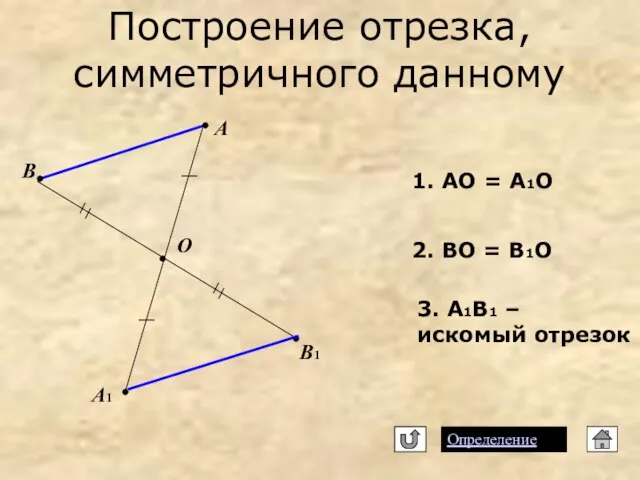
Построение отрезка, симметричного данному
Определение
А
А1
О
B
B1
1. АО = А1О
2. ВО = В1О
3. А1В1 – искомый отрезок

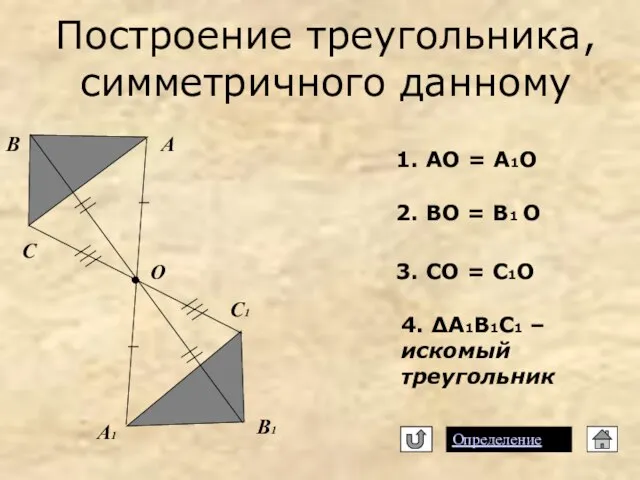
Построение треугольника, симметричного данному
Определение
О
А
А1
B
B1
C
C1
2. ВО = В1 О
1. АО = А1О
3. СО = С1О
4. ΔА1В1С1 – искомый треугольник

Задачи
1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О так, что АО≠ОВ. Симметричны ли точки А и В относительно точки О?
2. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
А
В
С
О
3. Постройте угол, симметричный углу ABC относительно центра О.
Проверь себя

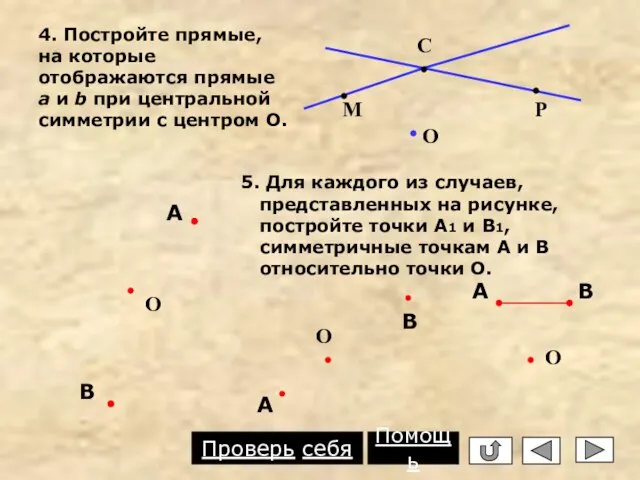
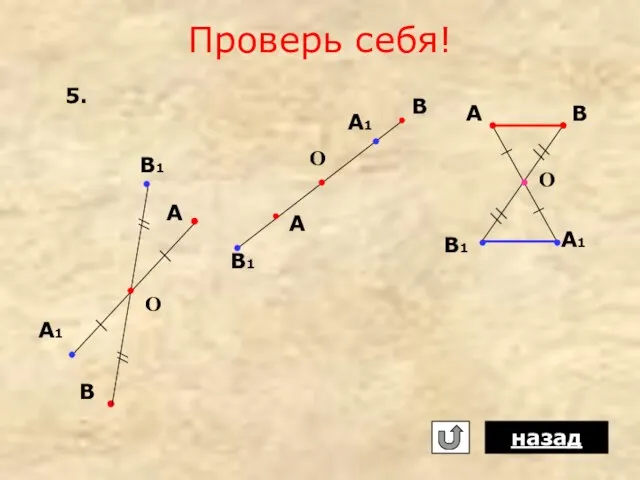
5. Для каждого из случаев, представленных на рисунке, постройте точки А1 и В1, симметричные точкам А и В относительно точки О.
В
А
А
В
А
В
О
О
О
О
С
М
Р
4. Постройте прямые, на которые отображаются прямые a и b при центральной симметрии с центром О.
Проверь себя
Помощь

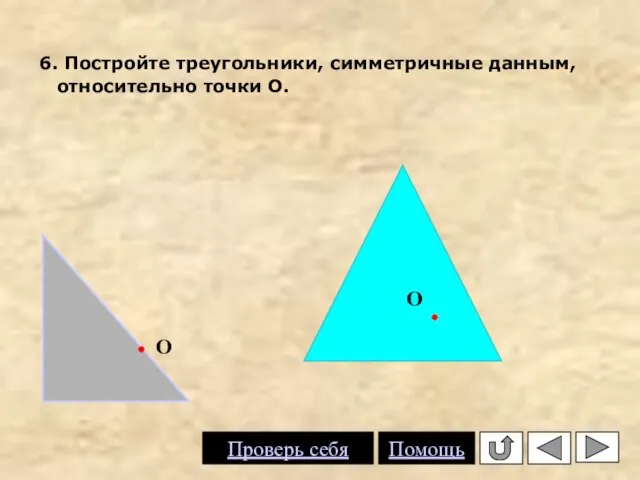
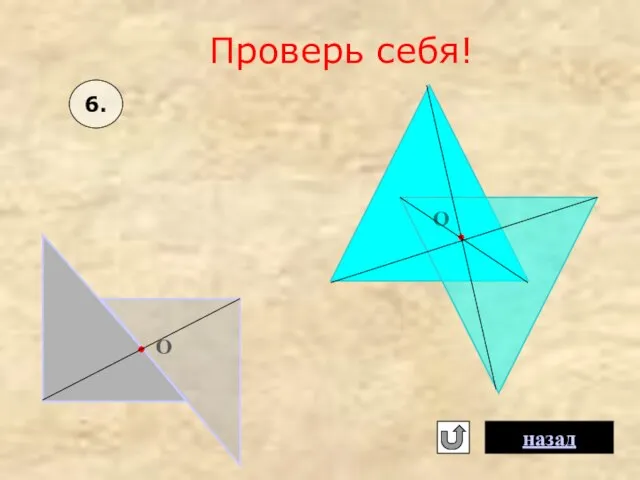
6. Постройте треугольники, симметричные данным, относительно точки О.
О
О
Проверь себя
Помощь

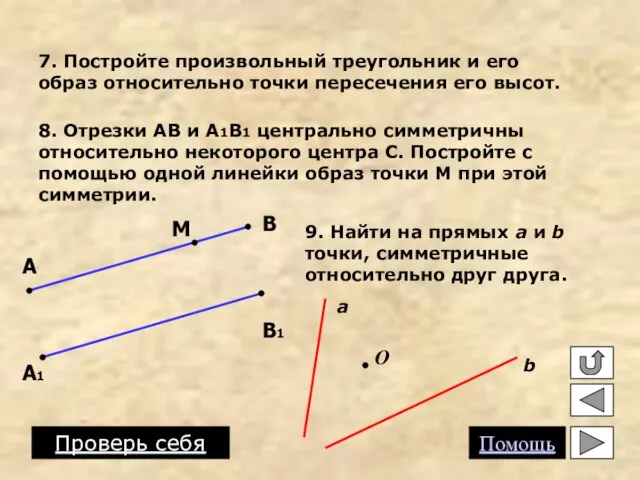
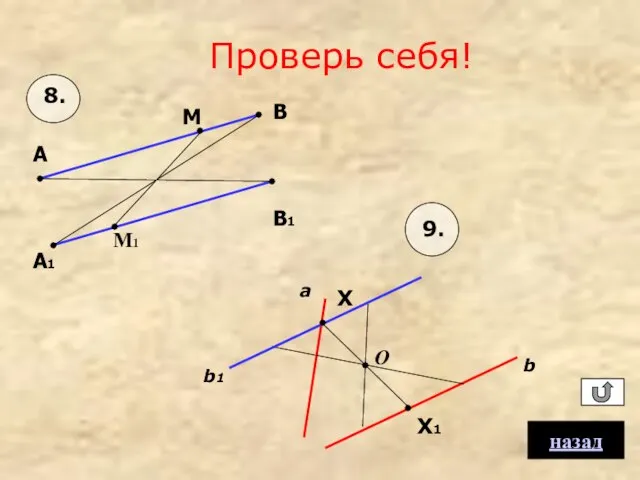
7. Постройте произвольный треугольник и его образ относительно точки пересечения его высот.
8. Отрезки АВ и А1В1 центрально симметричны относительно некоторого центра С. Постройте с помощью одной линейки образ точки М при этой симметрии.
А
В
А1
В1
М
9. Найти на прямых a и b точки, симметричные относительно друг друга.
a
b
O
Проверь себя
Помощь

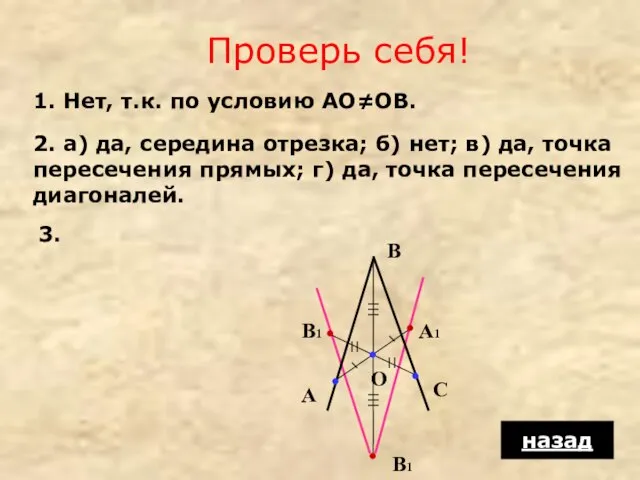
Проверь себя!
1. Нет, т.к. по условию АО≠ОВ.
2. а) да, середина отрезка; б) нет; в) да, точка пересечения прямых; г) да, точка пересечения диагоналей.
3.
А
В
С
О
В1
А1
В1
назад

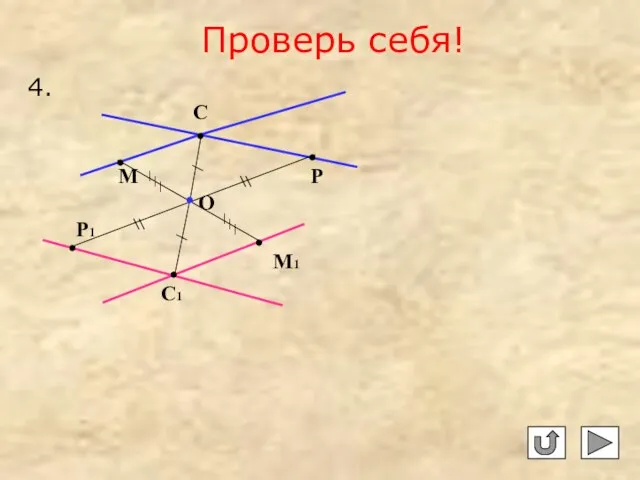
Проверь себя!
О
С
М
Р
4.
С1
Р1
М1

Проверь себя!
В
А
О
А
В
А
В
О
О
В1
А1
В1
А1
А1
В1
5.
назад

Проверь себя!
О
О
назад
6.

Проверь себя!
А
В
А1
В1
М
М1
8.
a
b
O
9.
Х
Х1
b1
назад