Центральные

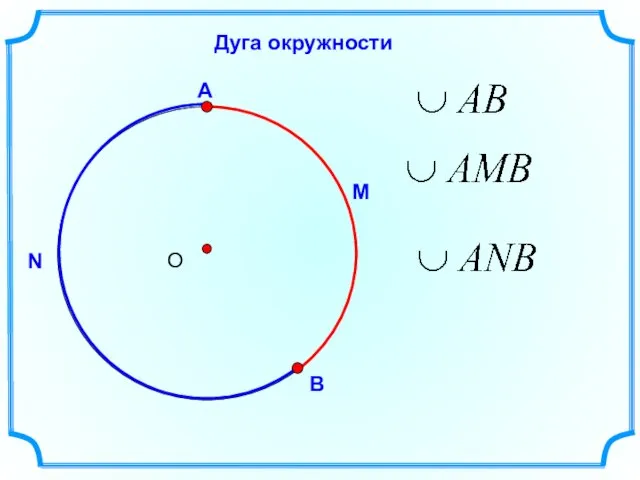
Дуга окружности
М

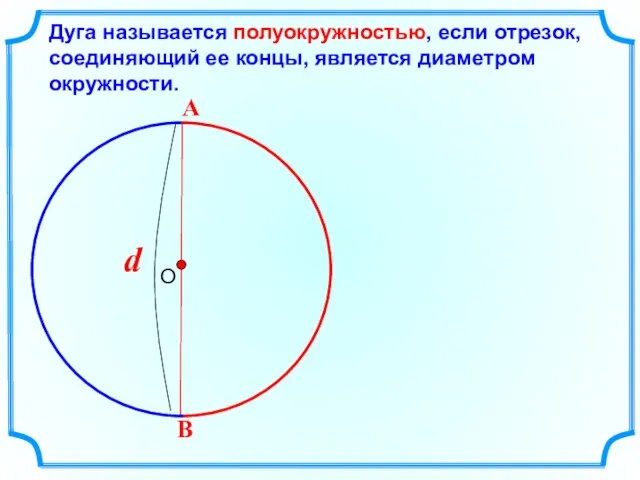
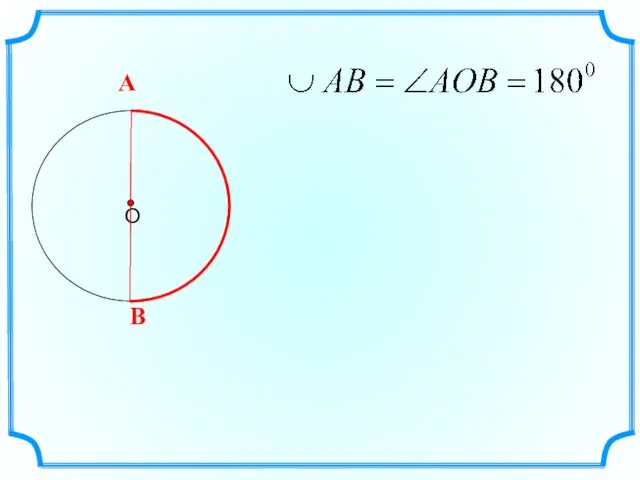
Дуга называется полуокружностью, если отрезок,
соединяющий ее концы, является диаметром окружности.

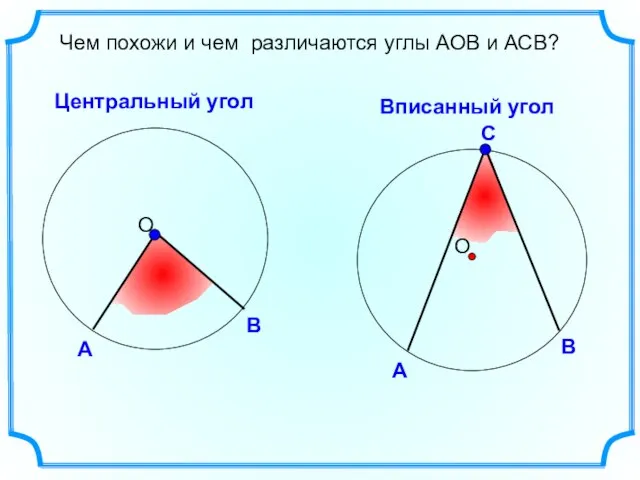
Чем похожи и чем различаются углы АОВ и АСВ?
Центральный угол
Вписанный угол

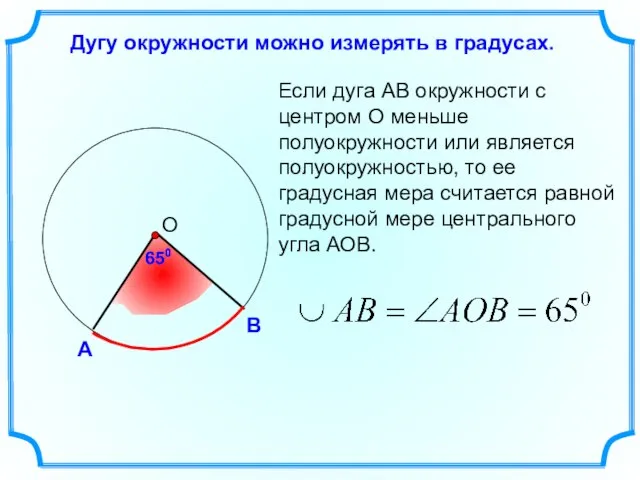
Дугу окружности можно измерять в градусах.
Если дуга АВ окружности с центром О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ.
650
650

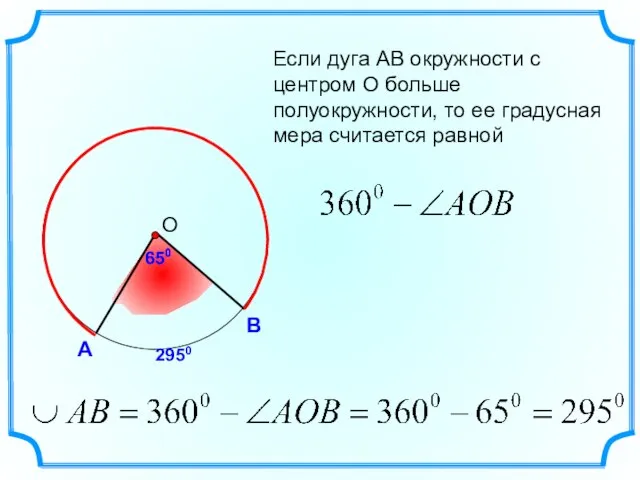
А
В
Если дуга АВ окружности с центром О больше полуокружности, то ее градусная мера считается равной
650
2950
650

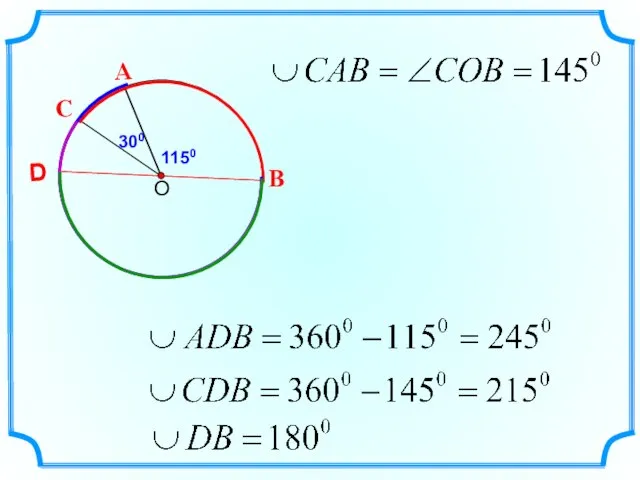
А
В
С
D
1150
300

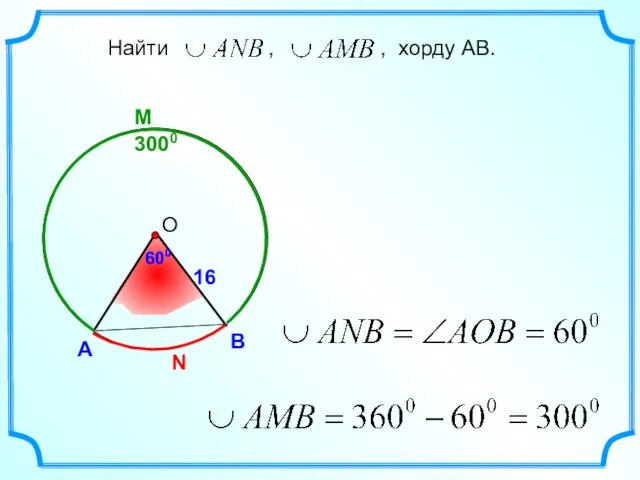
M
3000
600
А
В
Найти , , хорду АВ.
600
N
16

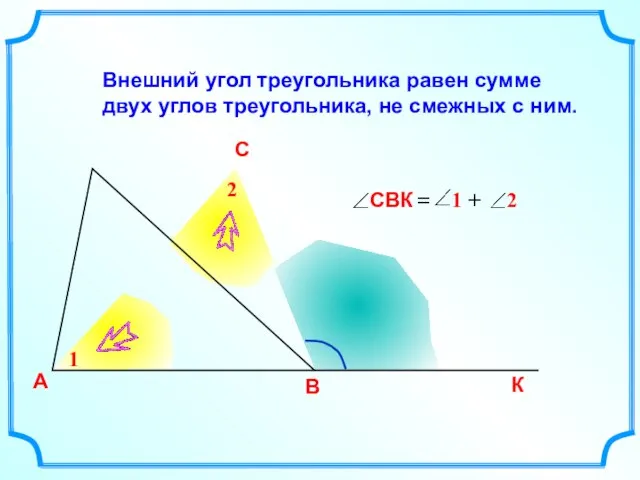
Внешний угол треугольника равен сумме
двух углов треугольника, не смежных с ним.
А
В
С
К
1
2
=
+