Начертательная геометрия. Лекция 3

Ортогональные проекции плоскости
Плоскость и способы задания ее на чертеже
Положение плоскости относительно плоскостей проекций
Прямая и точка в плоскости
Главные линии плоскости
Прямая и точка в плоскости
Относительное положение двух плоскостей

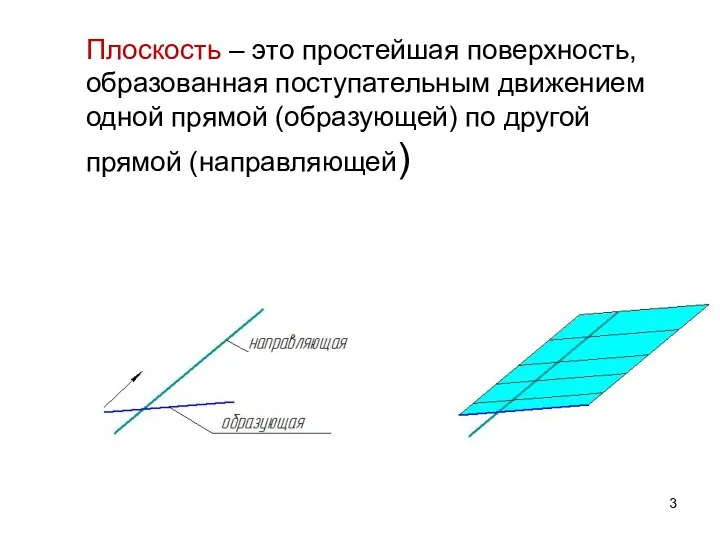
Плоскость – это простейшая поверхность, образованная поступательным движением одной прямой (образующей) по другой прямой (направляющей)

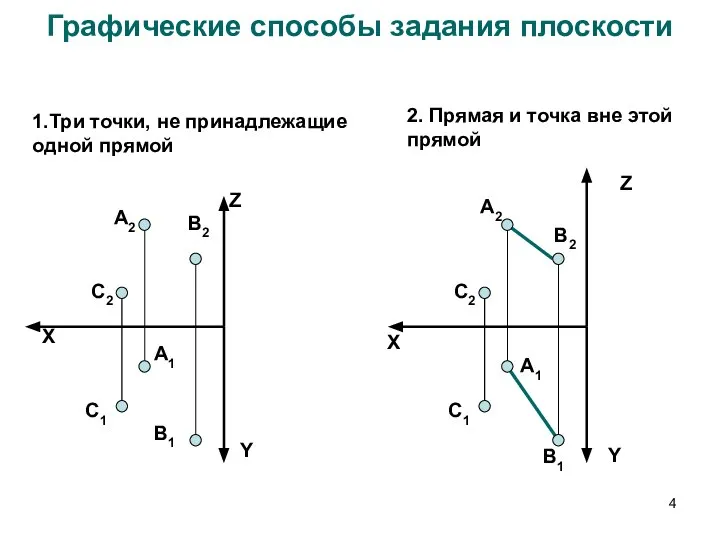
Графические способы задания плоскости
X
Z
Y
А2
А1
В1
C2
C1
В2
X
Y
C2
C1
1.Три точки, не принадлежащие одной прямой
2. Прямая и точка вне этой прямой
Z
А2
А1
В1
В2

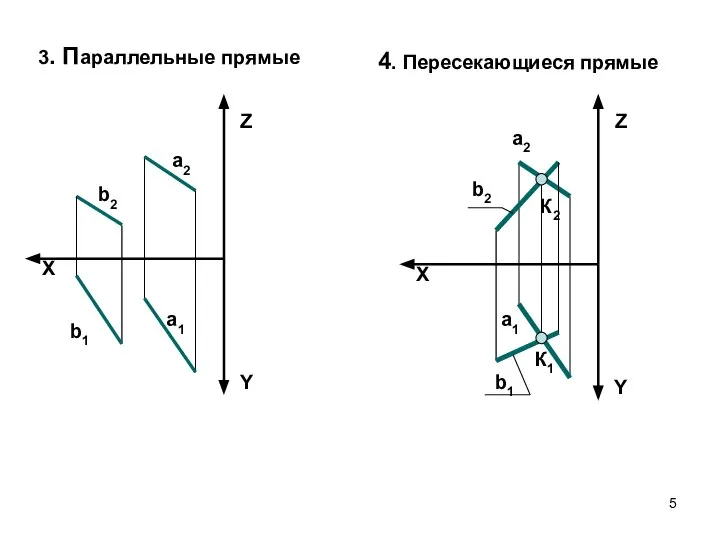
X
Z
Y
а2
а1
b2
b1
X
Z
Y
a2
a1
b2
b1
3. Параллельные прямые
4. Пересекающиеся прямые
К1
К2

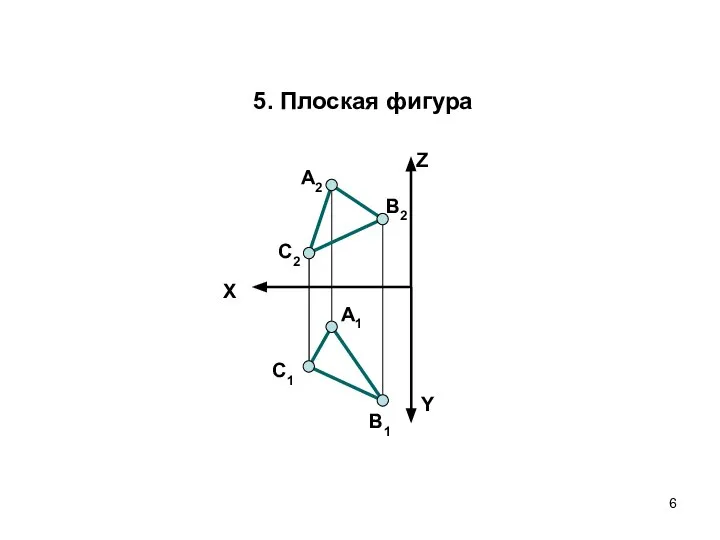
X
Z
Y
А2
А1
В1
C2
C1
В2
5. Плоская фигура

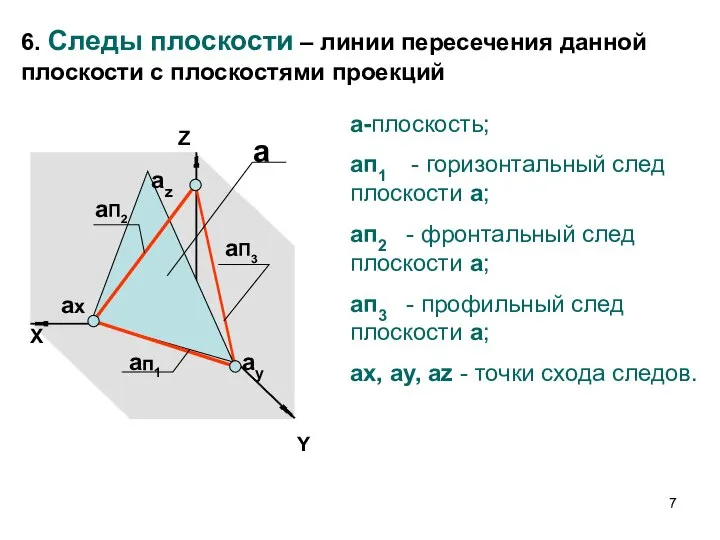
Y
Z
X
aп1
aП3
aП2
ax
ay
az
6. Следы плоскости – линии пересечения данной плоскости с плоскостями проекций
a
a-плоскость;
aп1 - горизонтальный след плоскости a;
aп2 - фронтальный след плоскости a;
aп3 - профильный след плоскости a;
ax, ay, az - точки схода следов.

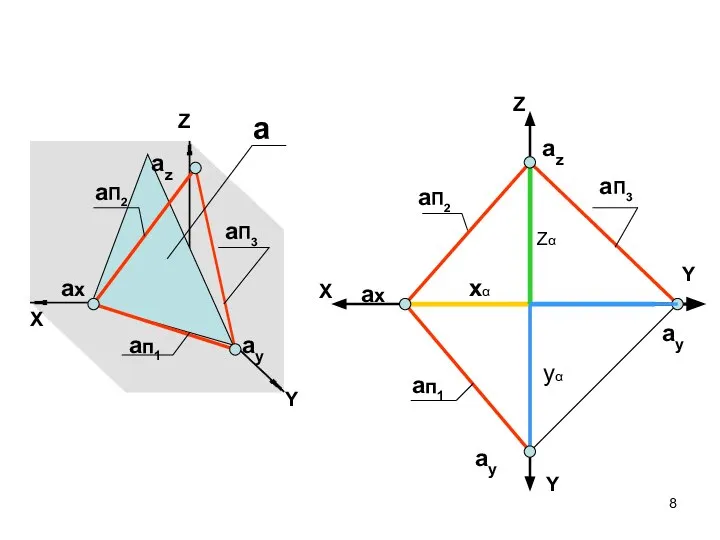
Z
X
Y
Y
aП2
aп1
aП3
ax
ay
az
Z
X
aп1
aП3
aП2
ax
ay
az
a
ay
Y
xα
yα
Zα

Особенности способа задания плоскости следами
Этот способ является частным случаем задания плоскости двумя пересекающимися прямыми
Каждый след совпадает со своей одноименной проекцией, другая проекция следа принадлежит оси проекций (вторую проекцию следа принято не обозначать)
Угол между следами плоскости на эпюре не равен углу между ее следами в пространстве
По расположению следов плоскости на эпюре легко представить расположение самой плоскости в пространстве

Положение плоскости относительно плоскостей проекций:
Параллельно – плоскости уровня;
Перпендикулярно – проецирующие плоскости
Под любым углом, отличным от прямого – плоскости общего положения

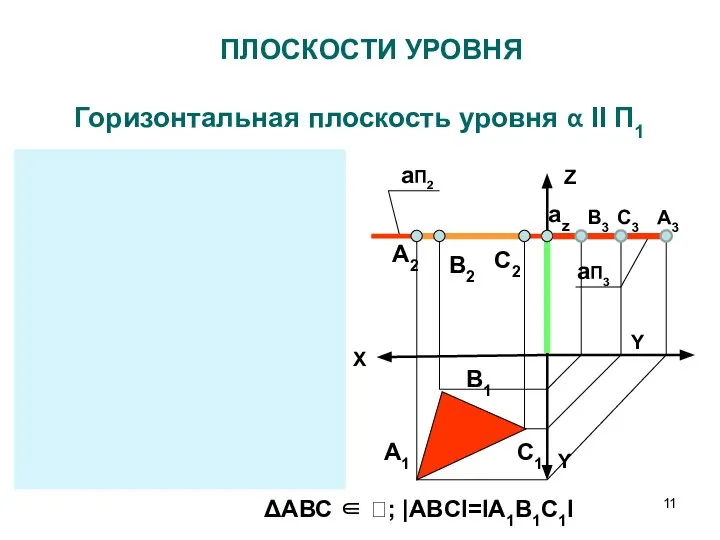
ПЛОСКОСТИ УРОВНЯ
Горизонтальная плоскость уровня α II П1
Z
X
Y
Y
aП2
aП3
az
Y
Z
X
α П3
αП2
α z
α
А1
В1
С1
А2
В2
С2
А1
С1
В1
А2
В2
С2
ΔАВС ∈ ; |ABCI=IA1B1C1I
В3 С3 А3

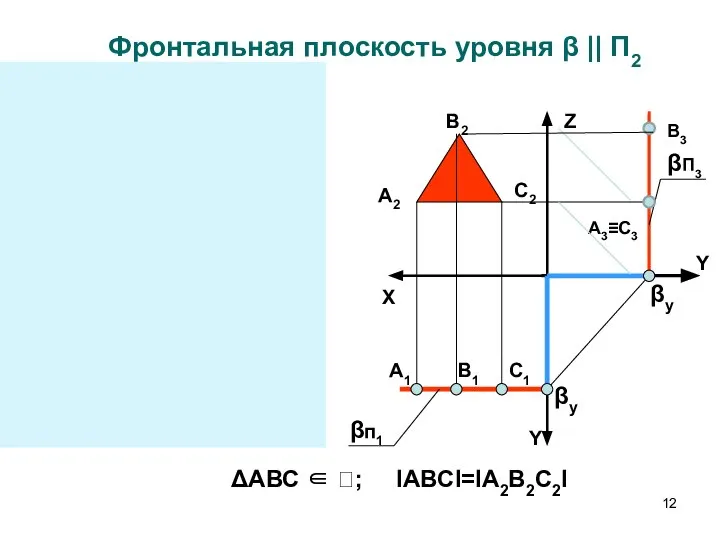
Z
X
Y
Y
βп1
βП3
βy
Y
Z
X
βп1
βП3
βy
βy
Фронтальная плоскость уровня β || П2
А1
В1
С1
С2
В2
А2
β
ΔАВС ∈ ; IABCI=IA2B2C2I
А3≡С3
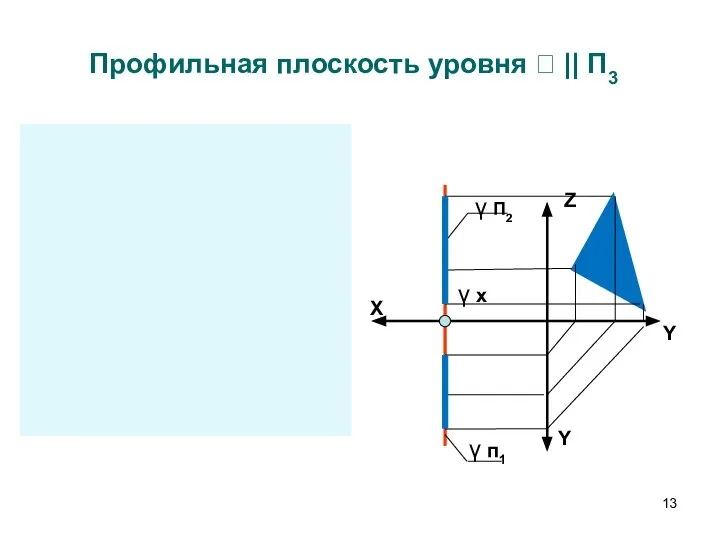
В3

Z
X
Y
Y
γ П2
γ п1
γ x
Z
X
γ п1
γ П2
γ x
γ
Профильная плоскость уровня  || П3
Y

Особенности чертежа плоскостей уровня
Фигуры, принадлежащие плоскостям уровня, проецируются в натуральную величину на параллельную плоскость проекций
На другие плоскости проекций фигуры, принадлежащие плоскостям уровня, проецируются в прямую линию

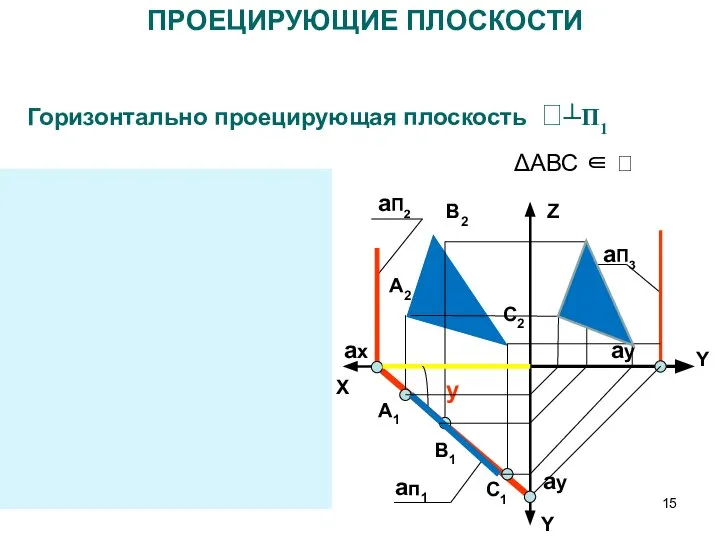
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ
Горизонтально проецирующая плоскость ┴П1
X
Y
Y
aП2
aП3
Z
X
aп1
aП2
ax
ax
Z
aп1
aП3
a
Y
ay
y
ay
ay
А1
В1
С1
А2
В2
С2
ΔАВС ∈ 

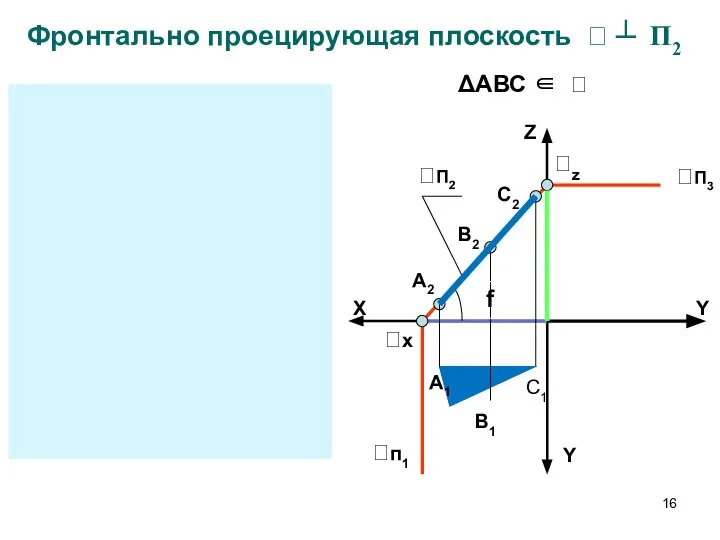
Фронтально проецирующая плоскость  ┴ П2
Z
X
Y
Y
П2
п1
x
Y
Z
X
П2
z

П3
П1
П3
z
x
А2
В2
С2
А1
В1
С1
f
ΔАВС ∈ 

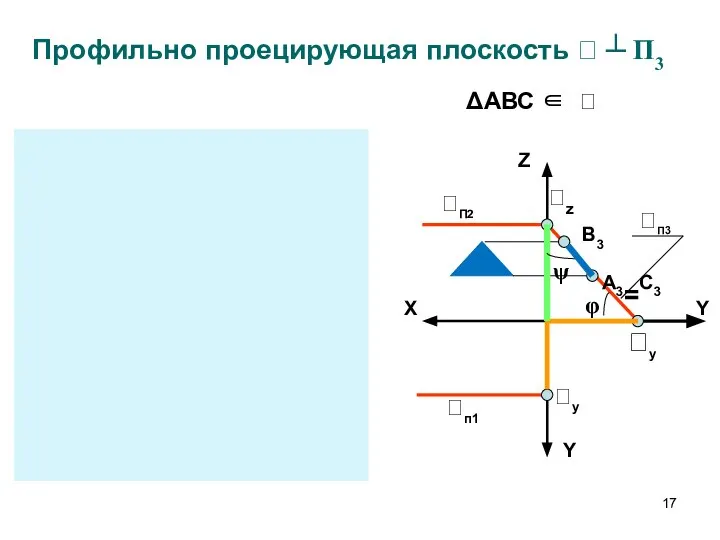
Профильно проецирующая плоскость  ┴ П3
Z
X
Y
Y
П2
п1
Y
Z
X
п1
П2
П3

П3
z
y
z
y
y
А3=С3
В3
φ
ψ
ΔАВС ∈ 

Фигуры, принадлежащие проецирующим плоскостям, на перпендикулярную плоскость проекций проецируются в прямую линию (вырожденная проекция)
Угол наклона между вырожденной проекцией и осями координат равен углу между заданной плоскостью и плоскостью проекций
Особенности чертежа проецирующих плоскостей

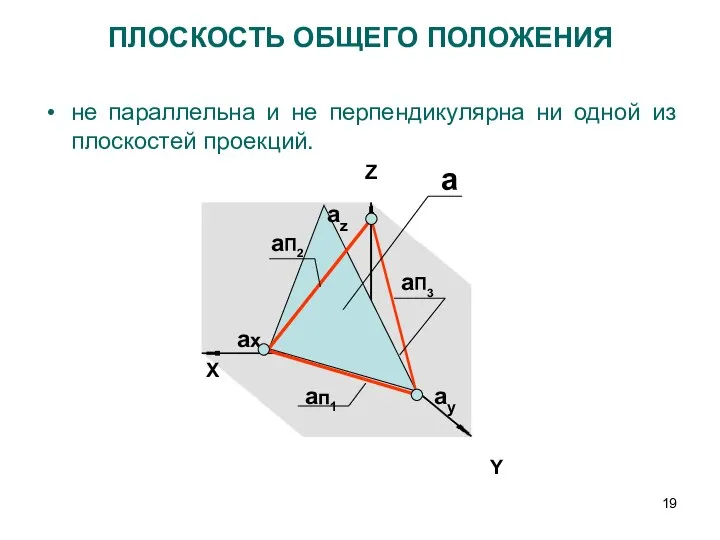
ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ
не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Y
Z
X
aп1
aП3
aП2
ax
ay
az
a

ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ
ПЛОСКОСТИ
Точка принадлежит плоскости, если она принадлежит прямой в этой плоскости
Прямая принадлежит плоскости, если она имеет с этой плоскостью две общие точки
Если прямая принадлежит плоскости, то её следы лежат на одноименных следах плоскости

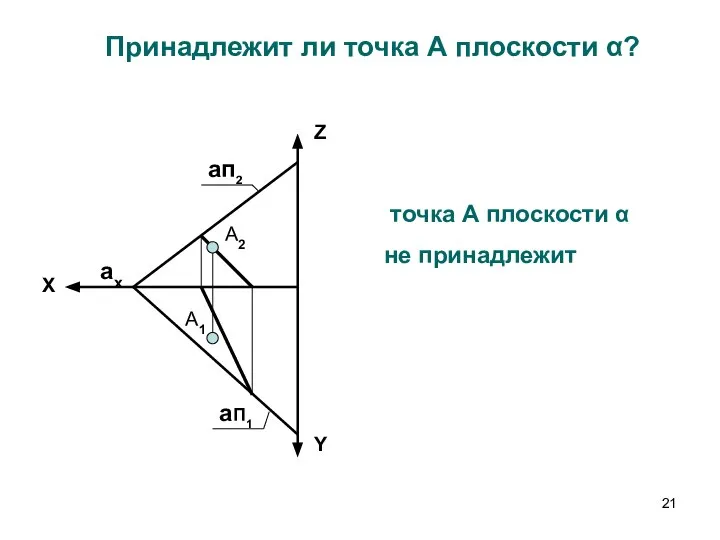
Принадлежит ли точка А плоскости α?
А2
А1
aп2
aП1
ax
Y
Z
X
точка А плоскости α
не принадлежит

Главные линии плоскости
Горизонталь плоскости
Фронталь плоскости
Линия ската плоскости

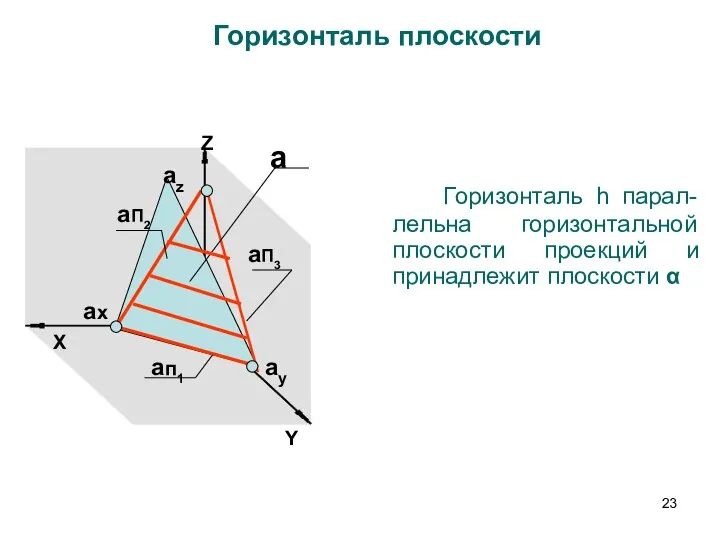
Z
X
aп1
aП3
aП2
ax
ay
az
a
Горизонталь плоскости
Y
Горизонталь h парал-лельна горизонтальной плоскости проекций и принадлежит плоскости α

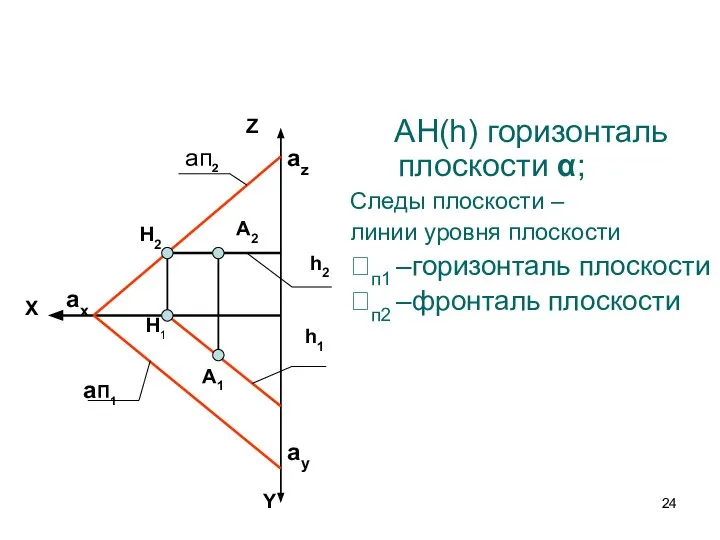
AН(h) горизонталь плоскости α;
Следы плоскости –
линии уровня плоскости
п1 –горизонталь плоскости
п2 –фронталь плоскости
aп2
aП1
Y
Z
X
ax
А2
А1
h2
h1
Н2
Н1
ay
az

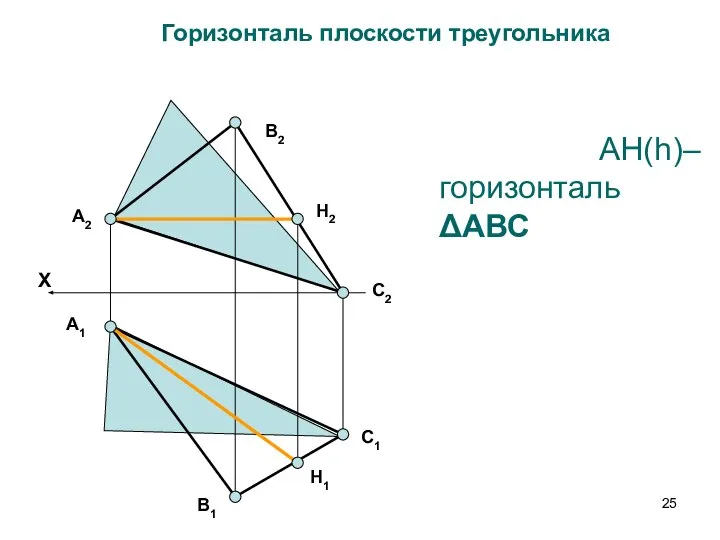
AH(h)– горизонталь ΔАВС
Горизонталь плоскости треугольника
А2
В2
С2
H2
В1
С1
А1
H1
X

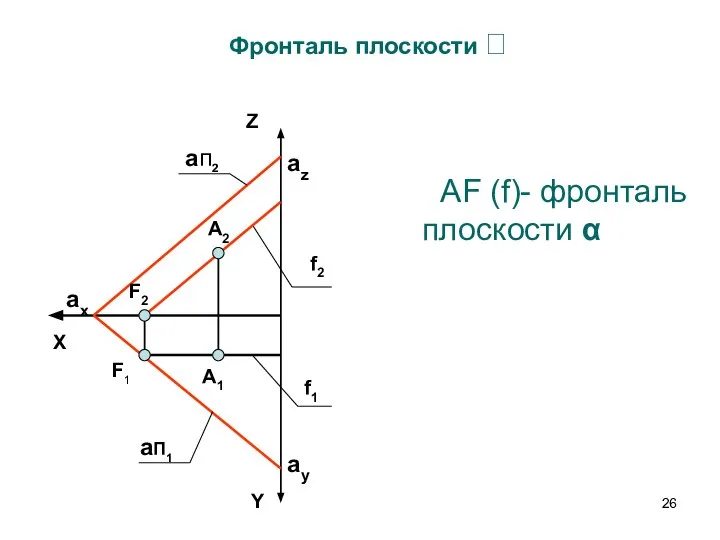
АF (f)- фронталь плоскости α
Фронталь плоскости 
aп2
aП1
Y
Z
ax
А2
А1
f2
f1
F2
F1
X
az
ay

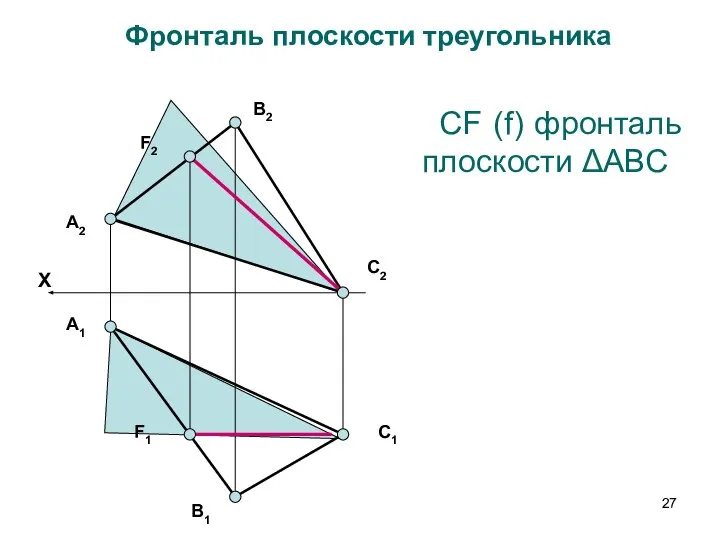
А2
F2
В2
С2
В1
С1
А1
F1
Фронталь плоскости треугольника
СF (f) фронталь плоскости ΔАВС
X

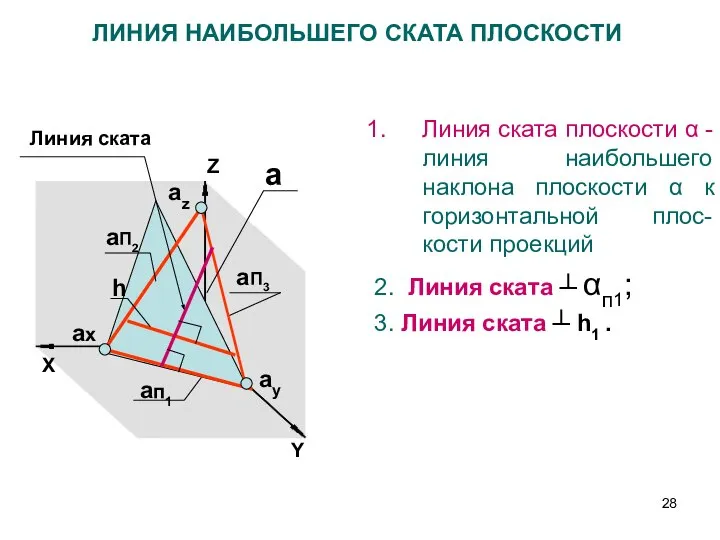
Z
X
aп1
aП3
aП2
ax
ay
az
a
ЛИНИЯ НАИБОЛЬШЕГО СКАТА ПЛОСКОСТИ
Линия ската плоскости α - линия наибольшего наклона плоскости α к горизонтальной плос-кости проекций
2. Линия ската ┴ αп1;
3. Линия ската ┴ h1 .
h
Y
Линия ската

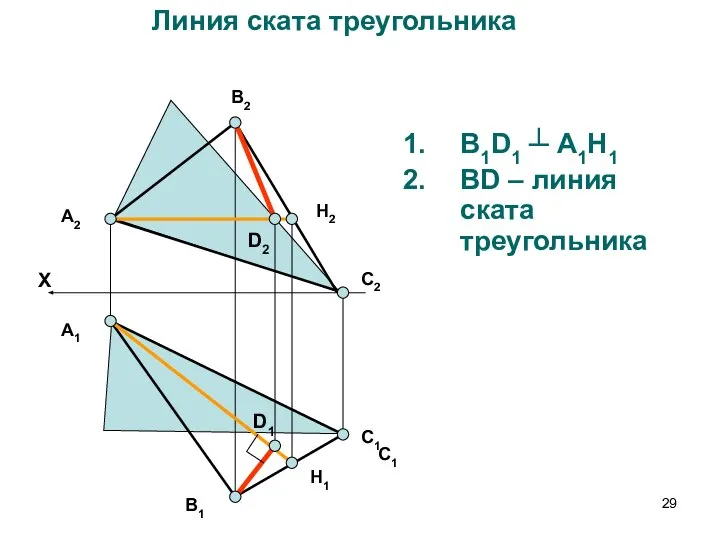
В1D1 ┴ А1H1
ВD – линия ската треугольника
А2
В2
С2
H2
В1
С1
А1
H1
X
Линия ската треугольника
D1
D2
С1

ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ
ПРЯМОЙ И ПЛОСКОСТИ,
ДВУХ ПЛОСКОСТЕЙ

Взаимное положение прямой и плоскости
Прямая принадлежит плоскости
Прямая параллельна плоскости
Прямая пересекает плоскость
Прямая перпендикулярна плоскости

Прямая параллельна плоскости,
если она параллельна хотя бы одной прямой, лежащей в этой плоскости

Пересечение прямой
с плоскостью
Аксиома:
Если прямая не принадлежит плоскости и не параллельна ей, то она эту плоскость пересекает

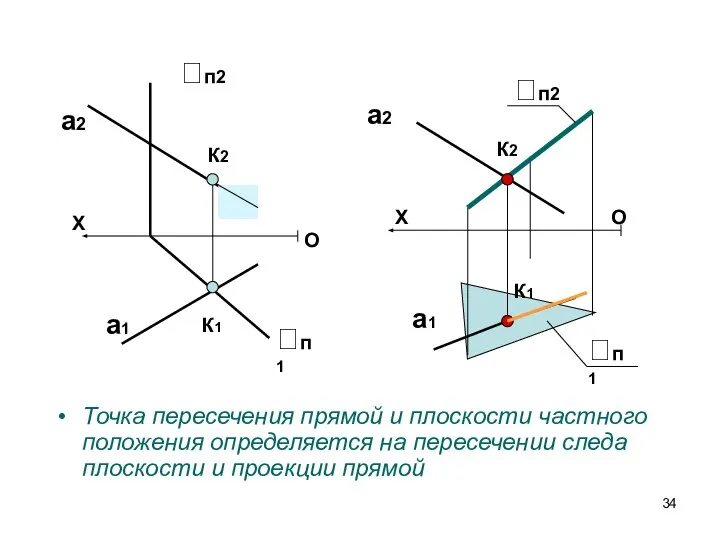
Точка пересечения прямой и плоскости частного положения определяется на пересечении следа плоскости и проекции прямой
X
O
a1
а2
п1
п2
К1
К2
X
O
a1
а2
п1
п2
К1
К2

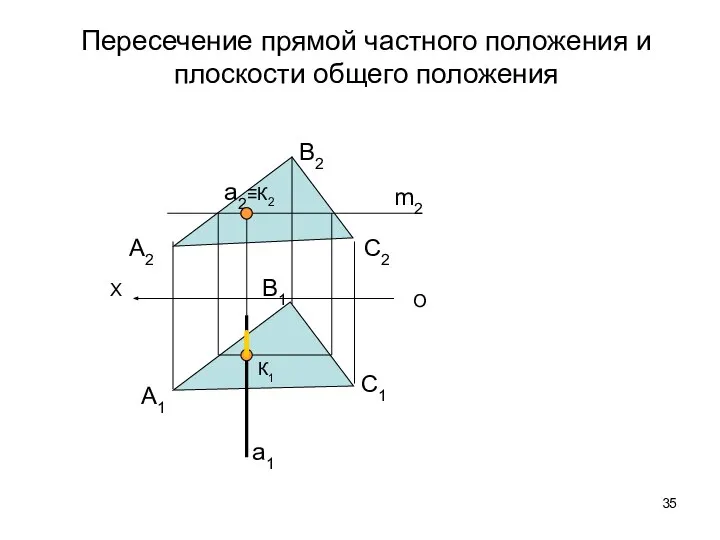
Пересечение прямой частного положения и плоскости общего положения
О
X
А2
В2
С2
А1
В1
С1
a1
a2
m2
К1
≡К2

СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ
1. Через прямую проводят плоскость частного положения α ┴ П1.
2. Определяют линию пересечения заданной плоскости и введенной плоскости α.
3. Определяют точку пересечения заданной прямой и построенной линии пересечения.
Это искомая точка пересечения заданной плоскости и прямой а.
4. Определяют видимость заданной прямой.

αп1
C1
22
A2
С2
B2
A1
B1
11
21
a1
a2
12
αп2
К2
К1
Видимость прямой определяют по конкурирующим точкам

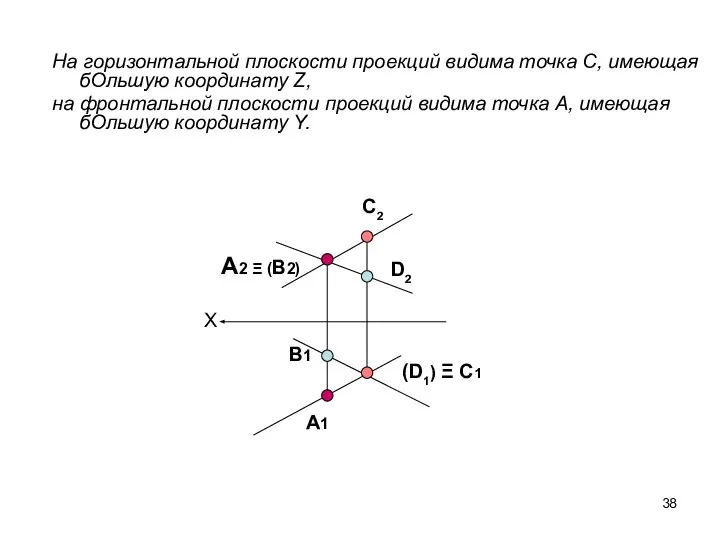
На горизонтальной плоскости проекций видима точка С, имеющая бОльшую координату Z,
на фронтальной плоскости проекций видима точка А, имеющая бОльшую координату Y.
А1
С2
D2
(D1) Ξ C1
В1
А2 Ξ (В2)
X

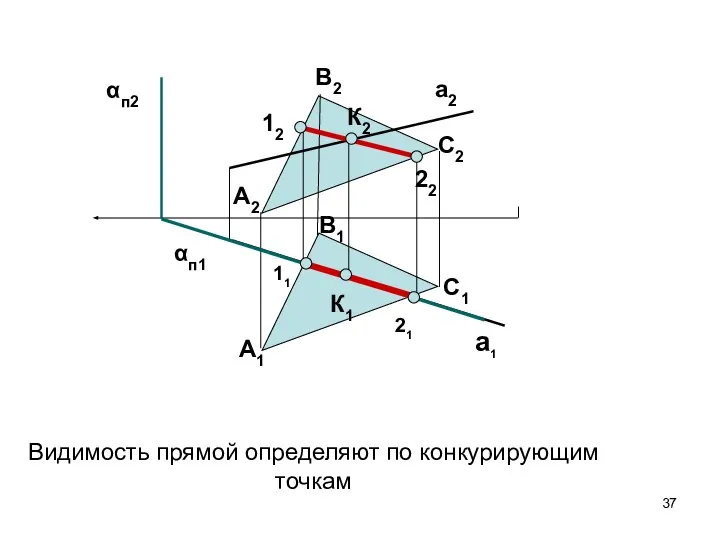
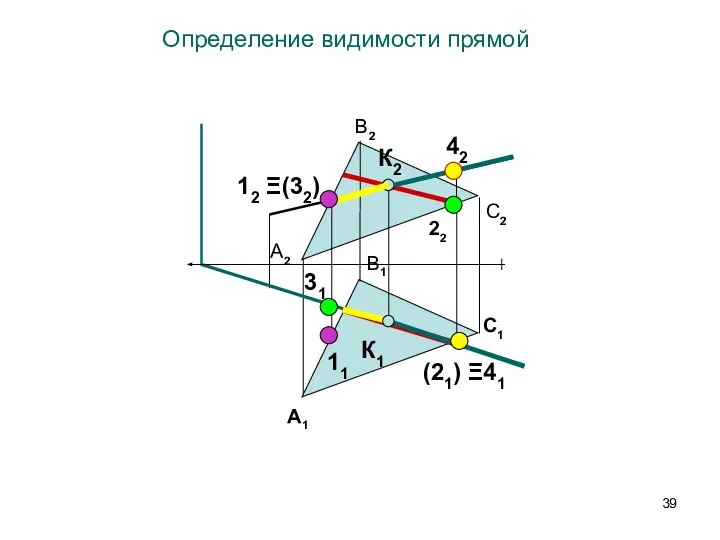
Определение видимости прямой
22
31
(21) Ξ41
12 Ξ(32)
42
11
C1
A2
С2
B2
A1
B1
К1
К2

Перпендикулярность прямой и плоскости
Теорема:
Прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости

Свойство перпендикуляра
к плоскости
Если прямая перпендикулярна плоскости, то
ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости (Г.П.Г.) или ее горизонтальному следу, а ее фронтальная проекция перпендикулярна фронтальной проекции фронтали плоскости (Ф.П.Ф.) или ее фронтальному следу

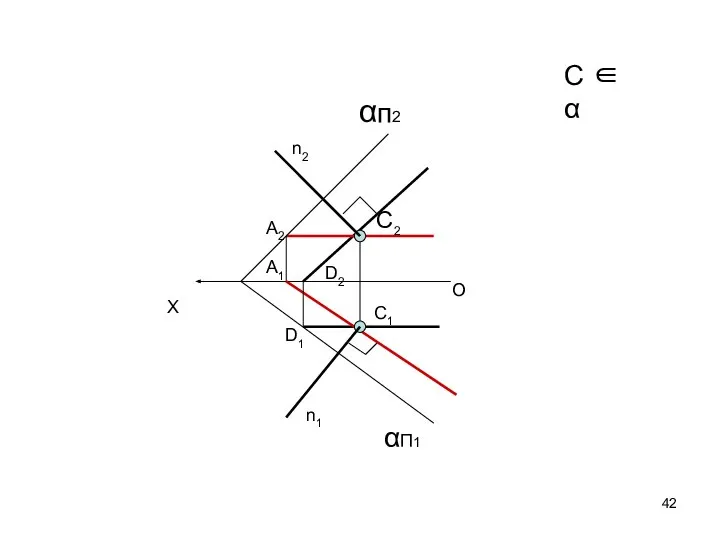
C ∈ α
αП1
O
X
αп2
С2
С1
А2
А1
D1
D2
n1
n2

Взаимное положение двух плоскостей
Две плоскости могут быть:
Параллельны друг другу;
Пересекаться друг с другом;
Перпендикулярны друг другу

Условие параллельности двух плоскостей
Теорема:
Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны друг другу.
Следствие:
Если плоскости параллельны, то их одноименные следы также параллельны

Пересечение двух плоскостей
Для построения линии пересечения двух плоскостей достаточно иметь две точки, общие к обеим плоскостям или одну общую точку и направление линии пересечения
Если плоскости заданы следами, то общие точки находятся в пересечении одноименных следов

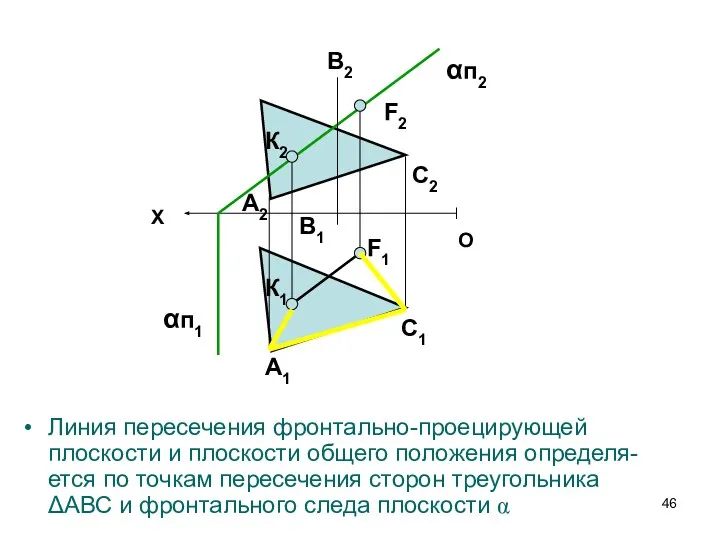
Линия пересечения фронтально-проецирующей плоскости и плоскости общего положения определя-ется по точкам пересечения сторон треугольника ΔАВС и фронтального следа плоскости α
X
O
К2
F2
F1
К1
A2
B2
C2
B1
A1
C1
αп1
αп2

Для построения линии пересечения плоскостей достаточно поочередно найти две точки пересечения двух ребер одной фигуры с другой фигурой.
Соединив эти точки, мы получим линию пересечения двух плоскостей.
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
ОБЩЕГО ПОЛОЖЕНИЯ

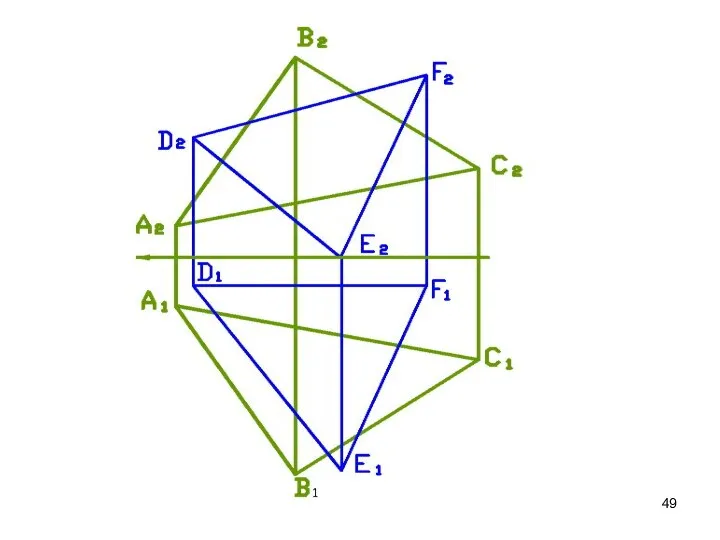
Задача
Построить линию пересечения треугольников ΔABC и ΔDEF.
A(100, 20, 20), B(65, 70, 70), C(10, 30,25),
D(90, 10, 55), E(45, 70, 0), F(20, 10, 65)

 АВС ∩ DE = К
DE ∈  ┴ П2
2.  АВС ∩ EF = L
EF ∈  ┴ П2

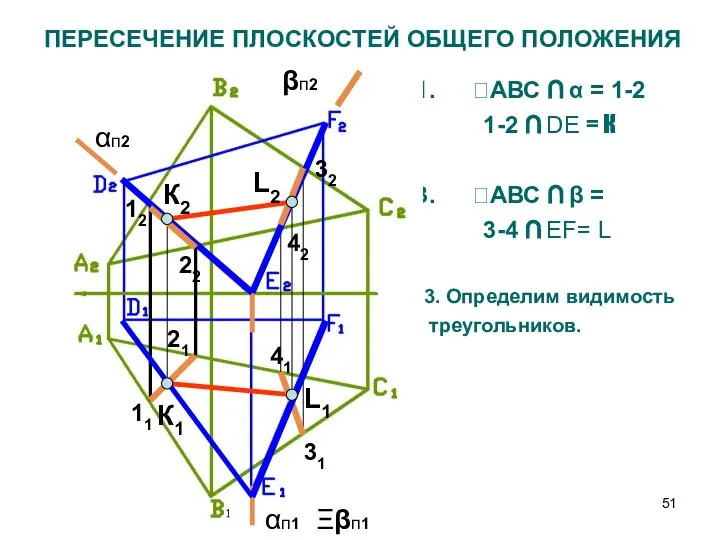
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
АВС ∩ α = 1-2
1-2 ∩ DE = К
АВС ∩ β =
3-4 ∩ EF= L
3. Определим видимость
треугольников.
αп2
αп1
К1
К2
βп2
Ξβп1
L2
L1
12
22
11
21
32
42
31
41

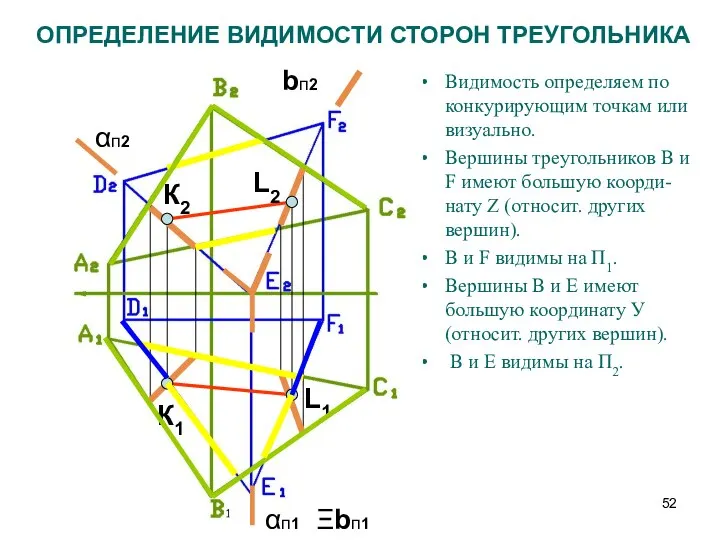
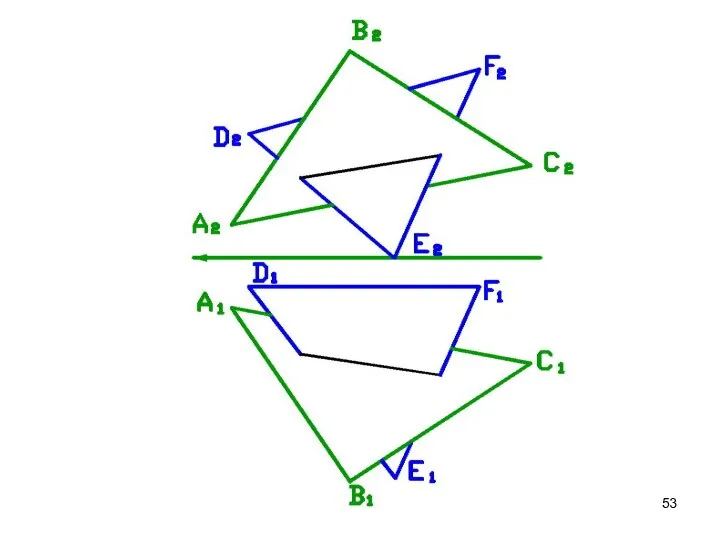
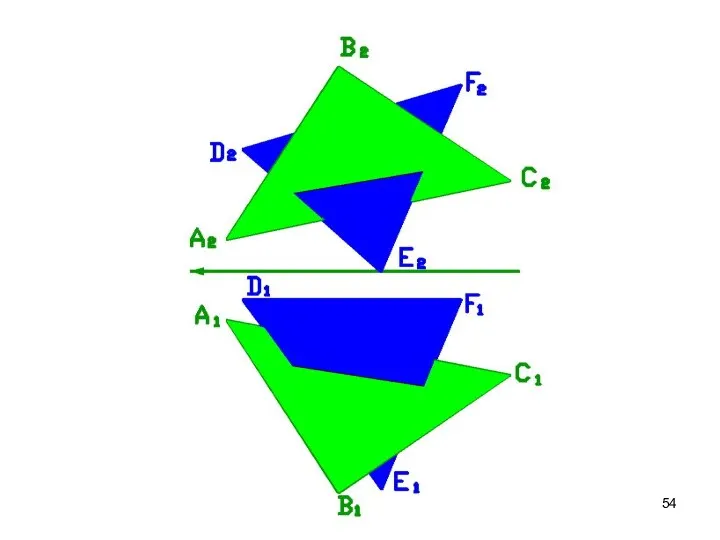
ОПРЕДЕЛЕНИЕ ВИДИМОСТИ СТОРОН ТРЕУГОЛЬНИКА
Видимость определяем по конкурирующим точкам или визуально.
Вершины треугольников В и F имеют большую коорди-нату Z (относит. других вершин).
В и F видимы на П1.
Вершины В и Е имеют большую координату У (относит. других вершин).
В и Е видимы на П2.
αп2
αп1
К1
К2
bп2
Ξbп1
L2
L1

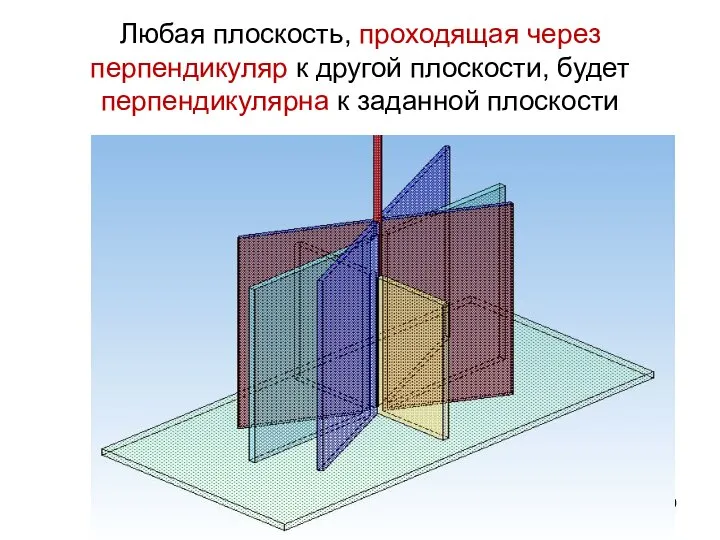
Взаимная перпендикулярность двух плоскостей
Аксиома:
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой плоскости

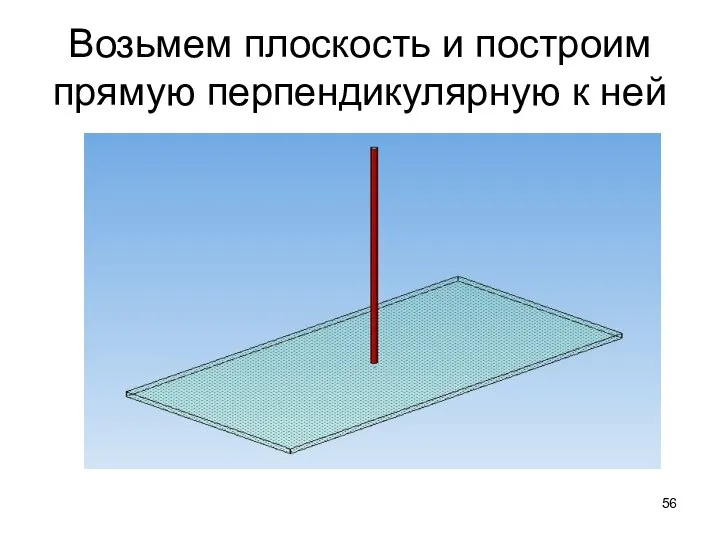
Возьмем плоскость и построим прямую перпендикулярную к ней

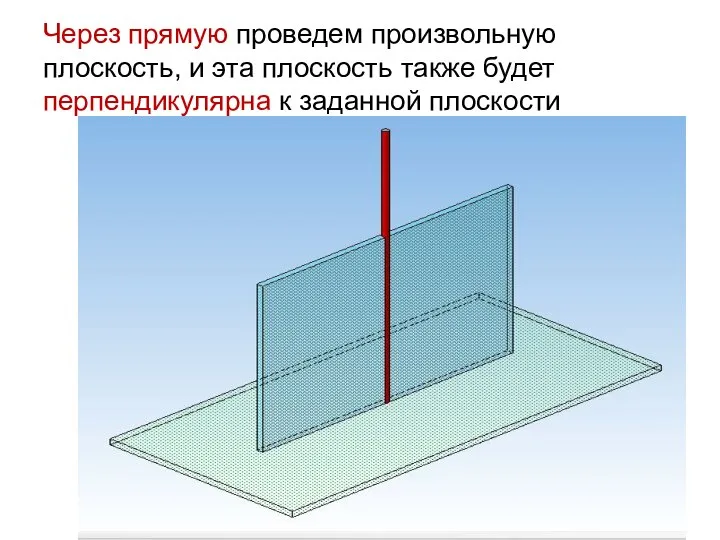
Через прямую проведем произвольную плоскость, и эта плоскость также будет перпендикулярна к заданной плоскости

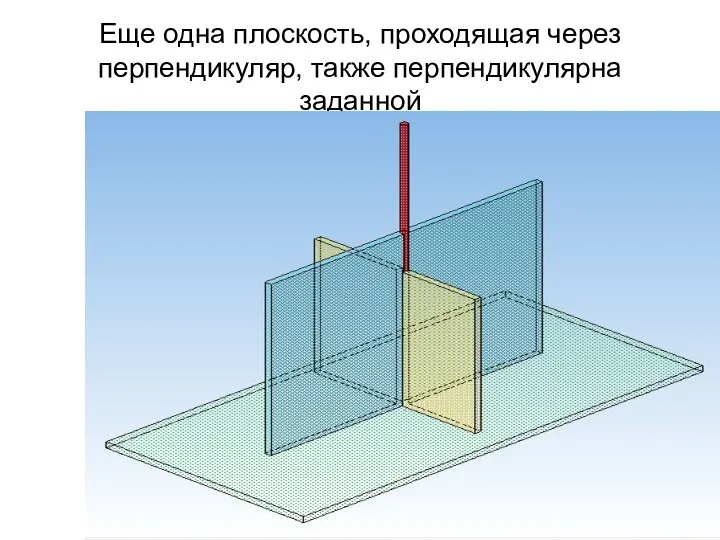
Еще одна плоскость, проходящая через перпендикуляр, также перпендикулярна заданной

Любая плоскость, проходящая через перпендикуляр к другой плоскости, будет перпендикулярна к заданной плоскости