Деревья (trees)

Задача построения филогенетического дерева
The time will come, I believe, though I shall not live to
see it, when we shall have fairly true genealogical trees
of each great kingdom of Nature.
Charles Darwin
Математическая задача – задача кластеризации,
использование теории графов и комбинаторной оптимизации
для того, чтобы на основе «грязных» биологических данных
получить разумное с точки зрения эксперта-биолога дерево.
Биологические задачи –
сравнение 3-х и более объектов
(кто на кого более похож .... )
реконструкция эволюции
(кто от кого, как и когда произошел…)

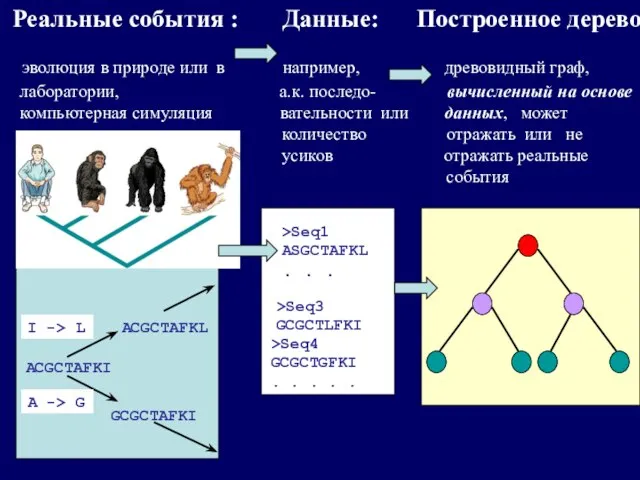
Реальные события : Данные: Построенное дерево
эволюция в природе или в например, древовидный граф,
лаборатории, а.к. последо- вычисленный на основе
компьютерная симуляция вательности или данных, может
количество отражать или не
усиков отражать реальные
события
>Seq4 GCGCTGFKI
. . . . .
>Seq1 ASGCTAFKL
. . .
>Seq3 GCGCTLFKI
A -> G
I -> L

Будни биоинформатика – деревья, деревья…

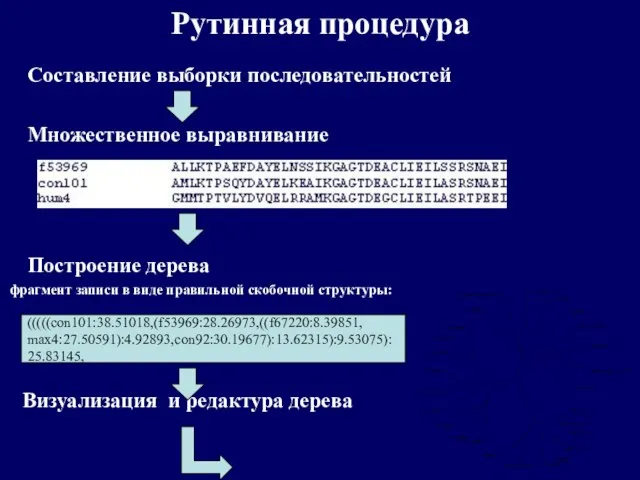
Рутинная процедура
Составление выборки последовательностей
Множественное выравнивание
Построение дерева
фрагмент записи в виде правильной скобочной структуры:
Визуализация и редактура дерева
(((((con101:38.51018,(f53969:28.26973,((f67220:8.39851,
max4:27.50591):4.92893,con92:30.19677):13.62315):9.53075):25.83145,

Основные термины

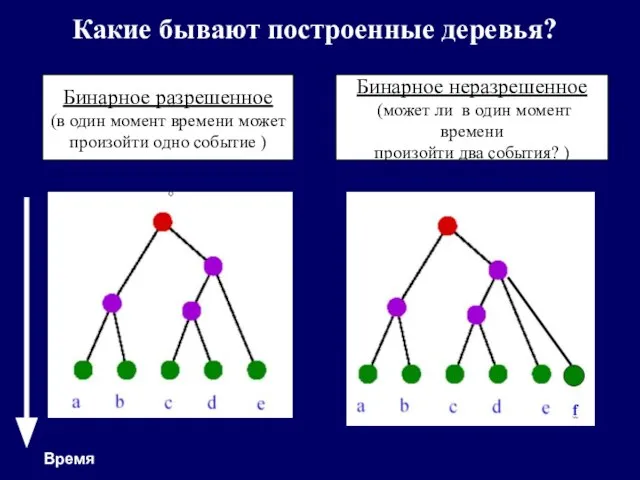
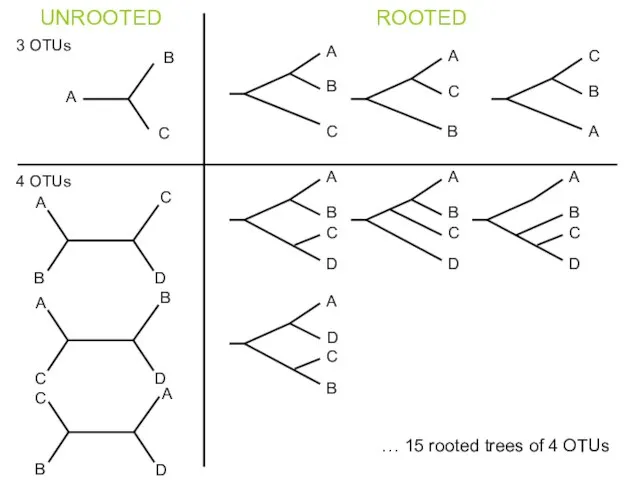
Какие бывают построенные деревья?
Бинарное разрешенное
(в один момент времени может
произойти одно событие )
Бинарное неразрешенное
(может ли в один момент времени
произойти два события? )
Время

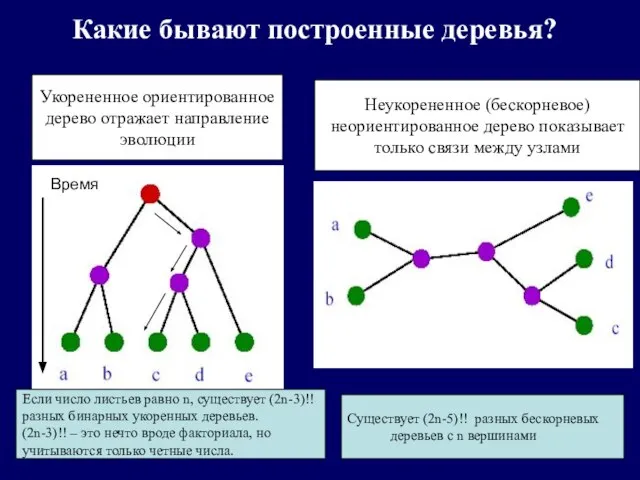
Какие бывают построенные деревья?
Укорененное ориентированное
дерево отражает направление
эволюции
Неукорененное (бескорневое)
неориентированное дерево показывает
только связи между узлами
Время
Если число листьев равно n, существует (2n-3)!!
разных бинарных укоренных деревьев.
(2n-3)!! – это нечто вроде факториала, но
учитываются только четные числа.
Существует (2n-5)!! разных бескорневых
деревьев с n вершинами

A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
… 15 rooted trees of 4 OTUs
3 OTUs
4 OTUs
UNROOTED
ROOTED

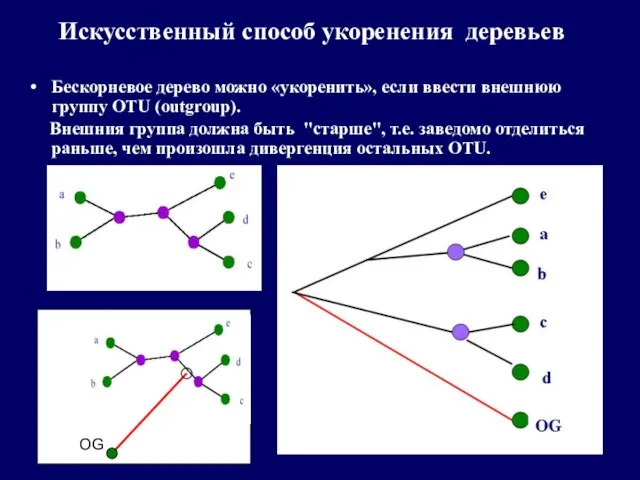
Искусственный способ укоренения деревьев
Бескорневое дерево можно «укоренить», если ввести внешнюю группу OTU (outgroup).
Внешния группа должна быть "старше", т.е. заведомо отделиться раньше, чем произошла дивергенция остальных OTU.

Какие бывают построенные деревья ?
Расстояние по дереву не то же самое, что
эволюционное расстояние между данными
Ультраметрические деревья
Корневое дерево, в котором для любых
листьев i и j расстояние D(i,j) – метка наименьшего
общего предка i и j .
В таком дереве все листья находятся на
одинаковом от корня, что соответствует
одинаковой скорости эволюции всех ветвей
Аддитивные деревья
Дерево, в котором для любых вершин i и j расстояние D(i,j) – это эволюционный путь от i к j . При этом расстояния от i и от j до их наименьшего общего предка могут сильно различаться.
Другие …
аддитивные
ультраметрические
Вообще говоря, строгое решение задачи
построения аддитивного дерева невозможно
(следует из свойства задачи)

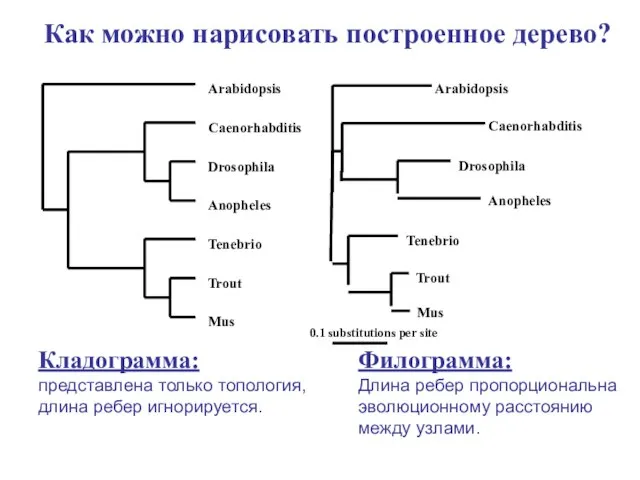
Филограмма:
Длина ребер пропорциональна эволюционному расстоянию между узлами.
Кладограмма:
представлена только топология, длина ребер игнорируется.
0.1 substitutions per site
Arabidopsis
Caenorhabditis
Drosophila
Anopheles
Tenebrio
Trout
Mus
Как можно нарисовать построенное дерево?

Основные алгоритмы построения филогенетических деревьев
Методы, основанные на оценке
расстояний (матричные методы):
Вычисляются эволюционные
расстояния между всеми вершинами
(OTUs) и строится дерево, в котором
расстояния между вершинами
наилучшим образом соответствуют
матрице попарных расстояний.
UPGMA (Unweighted Pair Group with Arithmetic Mean)
Ближайших соседей
(Neighbor-joining, NJ)
Символьно-ориентированные методы:
Наибольшего правдоподобия, Maximum likelihood, ML
Используется модель эволюции и строится дерево, которое наиболее правдоподобно при данной модели
Максимальной экономии (бережливости), maximum parsimony, MP
Выбирается дерево с минимальным количеством мутаций, необходимых для объяснения данных

Методы, основанные на оценке
расстояний
Дано:
М – матрица n x n,
где Mij>=0 , Mij – эволюционное расстояние
между листьями (OTU).
Задача:
Построить реберно взвешенное (an edge-weighted) дерево, где каждая вершина (лист) соответствует объекту из M , а расстояние, измеренное по дереву между вершинами (листьями) i and j соответствует Mij.

UPGMA
(алгоритм последовательной кластеризации)
Выбираем 2 наиболее похожие
вершины a, c.
Строим новый узел k такой, что D(a,k)=D(b,k)=D(a,c)/2.
Пересчитываем матрицу
попарных расстояний :
D(b, a or c) = [ D(b,a) + D(b,c) ] /2 = (8+9)/2=8.5
D(d, a or c) = [ D(d,a) + D(d,c) ] /2=(12+11)/2=11.5
Повторяем процедуру….
В конце концов получаем единственное ультраметрическое
укорененное дерево
=11.5

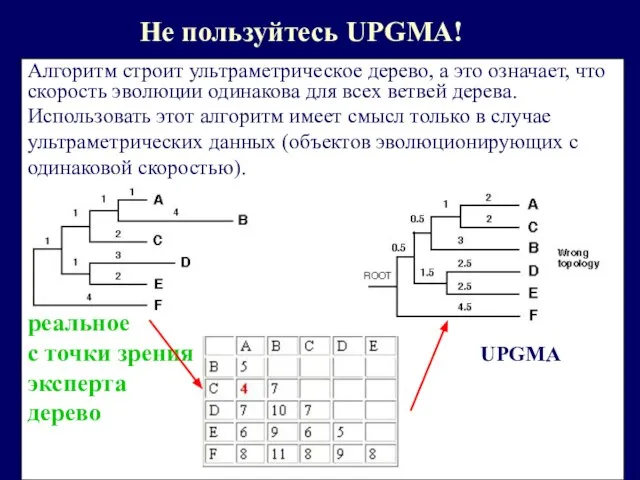
Не пользуйтесь UPGMA!
Алгоритм строит ультраметрическое дерево, а это означает, что
скорость эволюции одинакова для всех ветвей дерева.
Использовать этот алгоритм имеет смысл только в случае
ультраметрических данных (объектов эволюционирующих с
одинаковой скоростью).
реальное
c точки зрения UPGMA
эксперта
дерево

Метод ближайших соседей (Neighbor-joining, NJ)
1. Рисуем «звездное» дерево и будем "отщипывать" от него по паре
вершин, рассмотрим все возможные пары вершины.
пусть - «среднее» расстояние до других вершин.
2. Выберем 2 вершины i и j с минимальным значением
Mij – ui –uj
т.е. выбираем 2 узла, которые близки друг к другу, но далеки ото всех остальных.

Метод ближайших соседей (Neighbor-joining, NJ)
3. Кластер (i, j) – новый узел дерева Расстояние от i или от j до узла (i,j):
di, (i,j) = 0.5(Mij + ui-uj)
dj, (i,j) = 0.5(Mij + uj-ui)
т.е. длина ветви зависит от
среднего расстояния до других вершин.
4. Вычисляем расстояние от нового кластера до всех других
M(ij)k = Mik+Mjk – Mij
2
5. В матрице М убираем i и j и добавляем (i, j).
Повторяем, пока не останутся 2 узла......

Метод ближайших соседей (Neighbor-joining, NJ)
Строит бескорневое аддитивное дерево
Может работать с большим количеством данных
Достаточно быстрый алгоритм
Хорошо зарекомендовал себя на практике: если есть недвусмысленное с точки зрения эксперта дерево, то оно будет построено.
Используется при множественном выравнивании с помощью
программы ClustalW
Могут появиться ветви с длиной <0

Достоверность топологии. Bootstraps.
Создадим псевдоданные:
N множественных выравниваний той же длины, что и исходное, каждое из псевдовыравниваний - случайный набор столбцов из исходного.
Построим N деревьев:
на каждом внутреннем узле отметим долю
случаев из N, в которых появлялся
этот узел.
Обычно верят в топологию, если метки узлов на бутстрепном дереве больше 70-80% . Если меньше 30%, то не верим. В иных случаях – думаем…
Есть множественное выравнивание и
построенное по нему дерево.
Верим ли мы в топологию дерева?

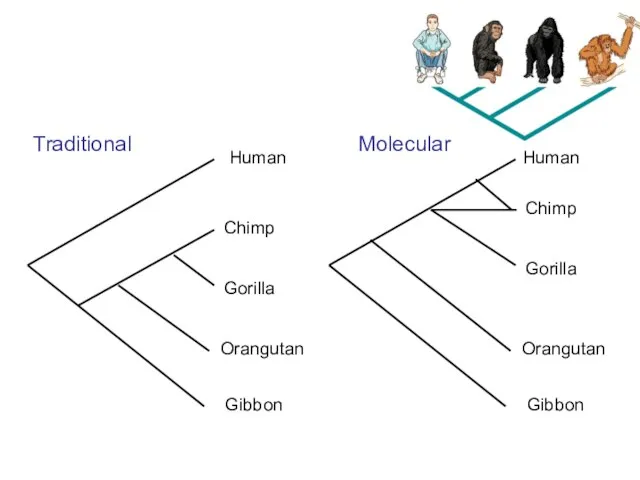
Human
Chimp
Gorilla
Orangutan
Gibbon
Traditional
Human
Chimp
Gorilla
Orangutan
Gibbon
Molecular