Содержание
- 2. Примитивы Точки Линии Прямоугольники (со сторонами, параллельными границам экрана) Многоугольники Шрифты Заливка областей Плоское отсечение
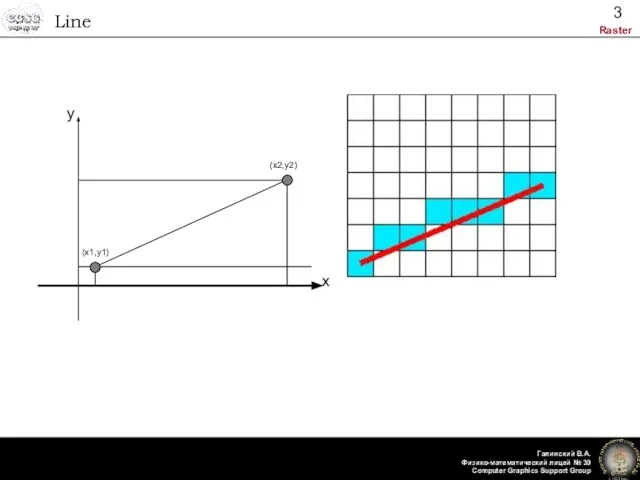
- 3. Line
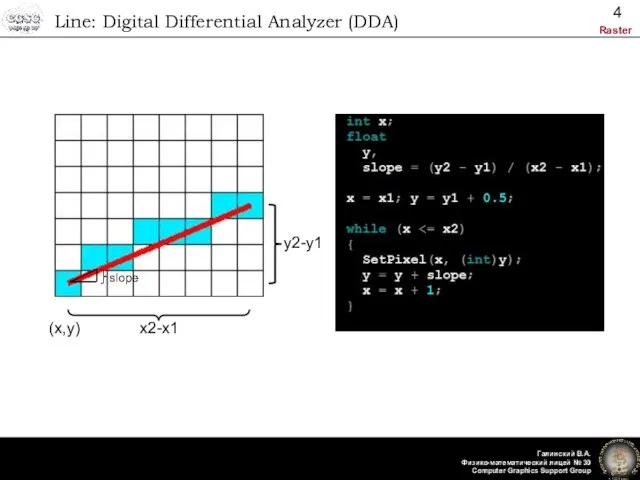
- 4. Line: Digital Differential Analyzer (DDA) (x,y) x2-x1 y2-y1 slope
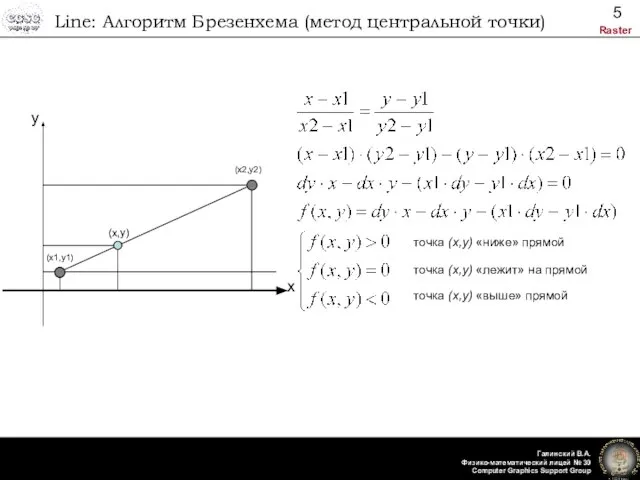
- 5. Line: Алгоритм Брезенхема (метод центральной точки) точка (x,y) «ниже» прямой точка (x,y) «лежит» на прямой точка
- 6. Line: Алгоритм Брезенхема (метод центральной точки) P(x,y) M(x+1,y+1/2) f(x,y) Подставляем точку M в функцию f: если
- 7. Line: Алгоритм Брезенхема (метод центральной точки) P(x,y) ME(x+2,y+1/2) f(x,y) Подставляем точку M в функцию f: если
- 8. Line: Алгоритм Брезенхема (метод центральной точки) P1(x1,y1) M0(x+1,y+1/2) f(x,y) Известны приращения f. Найдем первоначальное значение для
- 9. Line: Алгоритм Брезенхема (метод центральной точки) Сохранились вещественные числа. Сделаем замену: 2f = e Тогда помеченные
- 10. Line: Алгоритм Брезенхема (метод центральной точки)
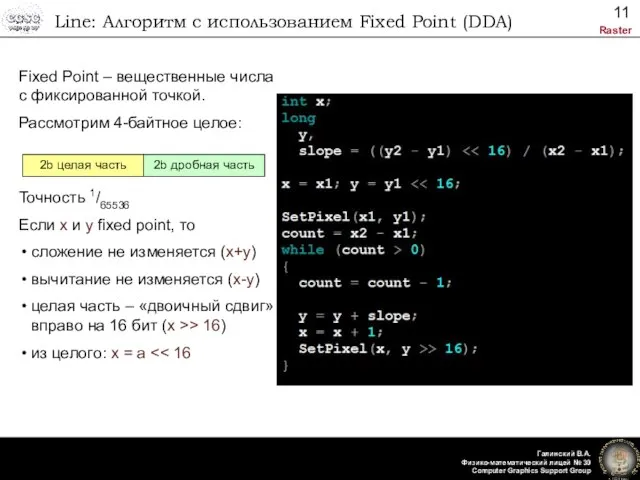
- 11. Line: Алгоритм с использованием Fixed Point (DDA) Fixed Point – вещественные числа с фиксированной точкой. Рассмотрим
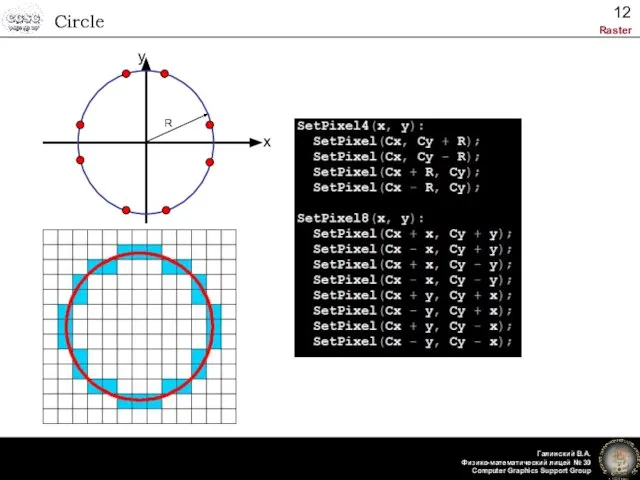
- 12. Circle R
- 13. Circle: Алгоритм Брезенхема (метод центральной точки) Подставляем точку M в функцию f: если f(M) >= 0
- 14. Circle: Алгоритм Брезенхема (метод центральной точки) P(x,y) M E SE MSE ME f(x,y) Изменения значения f(M)
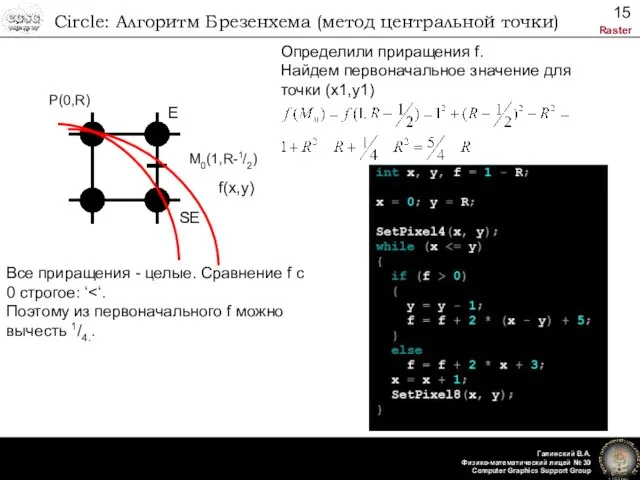
- 15. Circle: Алгоритм Брезенхема (метод центральной точки) Определили приращения f. Найдем первоначальное значение для точки (x1,y1) Все
- 16. Circle: Алгоритм Брезенхема (метод центральной точки) Дополнительная оптимизация: Просчитаем изменение приращений по направлениям E и SE
- 17. Circle: Алгоритм Брезенхема (метод центральной точки)
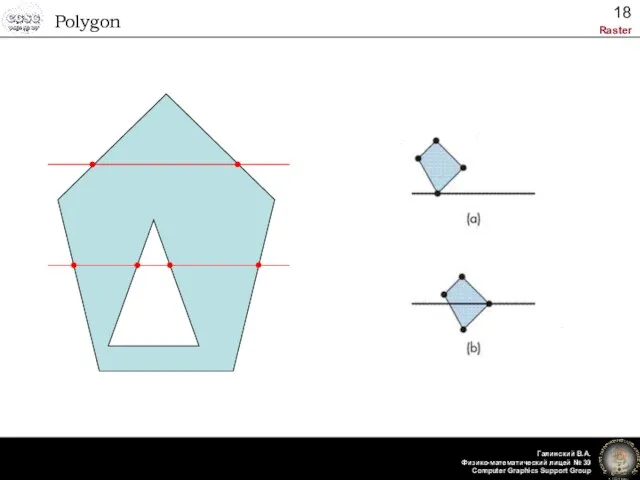
- 18. Polygon
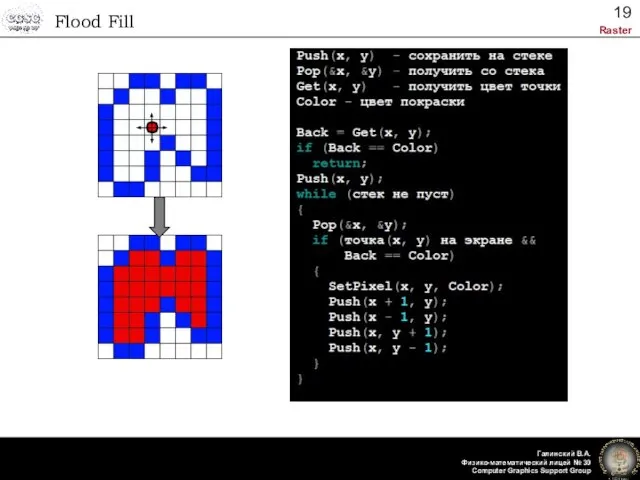
- 19. Flood Fill
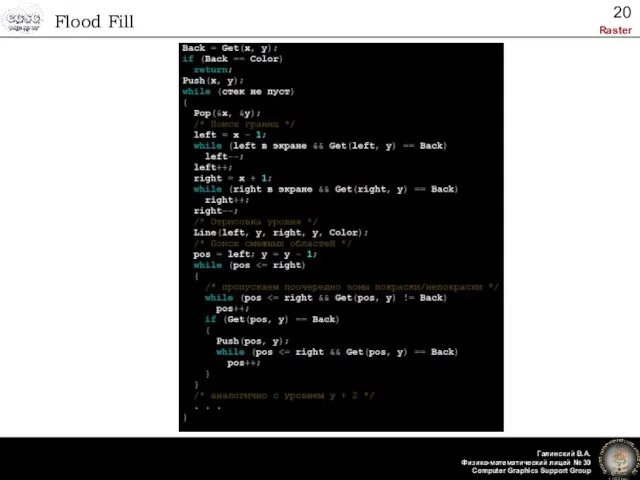
- 20. Flood Fill
- 21. Text Шрифты Растровые Векторные Контурные
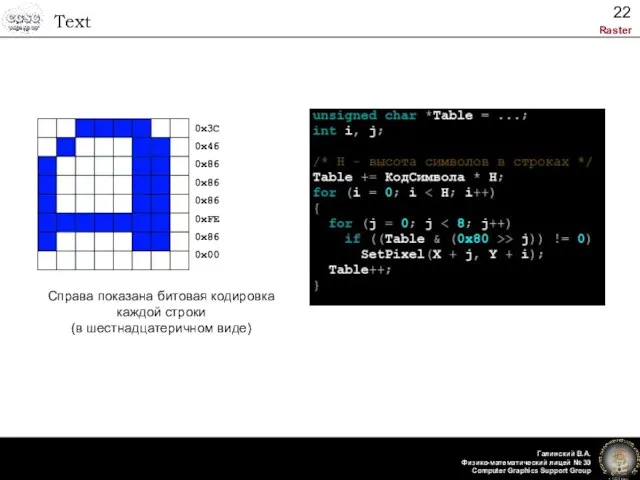
- 22. Text 0x3C 0x46 0x86 0x86 0x86 0xFE 0x86 0x00 Справа показана битовая кодировка каждой строки (в
- 24. Скачать презентацию











 ГАЗПРОМ - МЕЧТЫ СБЫВАЮТСЯ ?
ГАЗПРОМ - МЕЧТЫ СБЫВАЮТСЯ ? Мой профессиональный выбор
Мой профессиональный выбор Магистерская программа «Технологическая подготовка производства приборов и систем»
Магистерская программа «Технологическая подготовка производства приборов и систем» Федеральный государственный образовательный стандарт общего образования в контексте государственной политики в образовании
Федеральный государственный образовательный стандарт общего образования в контексте государственной политики в образовании Выполнил: Круглов Владимир, 8 класс МОУ СОШ №2
Выполнил: Круглов Владимир, 8 класс МОУ СОШ №2 Мотивация к обучению. Лекция 3
Мотивация к обучению. Лекция 3 Значение животных в природе и в жизни человека
Значение животных в природе и в жизни человека В гостях у сказки (театральная деятельность)
В гостях у сказки (театральная деятельность) Юридическая клинка МГЮА Подготовил : Студент 3-го курса Сорокин А.А. группа ю -123б
Юридическая клинка МГЮА Подготовил : Студент 3-го курса Сорокин А.А. группа ю -123б Добро пожаловать в АО ННК-Хабаровский НПЗ
Добро пожаловать в АО ННК-Хабаровский НПЗ Презентация на тему Уменьшаемое. Вычитаемое. Разность (1 класс)
Презентация на тему Уменьшаемое. Вычитаемое. Разность (1 класс) Безударные гласные и е 1 класс
Безударные гласные и е 1 класс Проектирование страниц интерфейса в Adobe Fireworks Александр Хмелевский UI Modeling Company. - презентация
Проектирование страниц интерфейса в Adobe Fireworks Александр Хмелевский UI Modeling Company. - презентация Об обучении на дому детей с ограниченными возможностями здоровья и детей-инвалидов
Об обучении на дому детей с ограниченными возможностями здоровья и детей-инвалидов Презентация на тему Дельфины
Презентация на тему Дельфины  Праздник весны в группе "Непоседы"
Праздник весны в группе "Непоседы" СОЗДАНИЕ МЕХАНИЗМОВ СТИМУЛИРОВАНИЯ РАЗВИТИЯ АЛЬТЕРНАТИВНОЙ ЭНЕРГЕТИКИ
СОЗДАНИЕ МЕХАНИЗМОВ СТИМУЛИРОВАНИЯ РАЗВИТИЯ АЛЬТЕРНАТИВНОЙ ЭНЕРГЕТИКИ Современное состояние олигофренопедагогики в Дании
Современное состояние олигофренопедагогики в Дании Клодт Петр Карлович Укрощение коня
Клодт Петр Карлович Укрощение коня Ландшафтный бизнес и его составляющие части
Ландшафтный бизнес и его составляющие части Газированные напитки и лимонады с вредными добавками
Газированные напитки и лимонады с вредными добавками Тарифное регулирование
Тарифное регулирование Презентация на тему Звуки х, х. Буквы Х х
Презентация на тему Звуки х, х. Буквы Х х  КАСКО. Демократичное
КАСКО. Демократичное Договоры о передаче прав патентообладателя Презентацию подготовила студентка Гусева А.
Договоры о передаче прав патентообладателя Презентацию подготовила студентка Гусева А. Управление техносферной безопасностью. Управление, процесс и принципы управления, документы по управлению. (Лекция 1)
Управление техносферной безопасностью. Управление, процесс и принципы управления, документы по управлению. (Лекция 1) В.П. Гергель, О.А.Кузенков
В.П. Гергель, О.А.Кузенков Газоперекачивающий аппарат с авиаприводом
Газоперекачивающий аппарат с авиаприводом