ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

Число — единица счёта, выражающая количество, а цифра — знак (символ), обозначающий значение числа.
Развитие понятия о числе

ТЕСТ
Перейди по ссылке и пройди тест:

Множества
Множеством называют набор объектов, обладающие общим для всех характеристическими свойствами. Множество задается либо перечислением всех его элементов либо указанием некоторого свойства, такого, что все его элементы множества обладают этим свойством. Так же следует помнить, что любое множество А может содержать подмножество В, или находиться в подмножестве множества С.

Основные математические обозначения

Операции над множествами

Числовые множества

Практические задания:
Дано некоторое множество, состоящее из трех элементов: A = {a, b, c} . Найдите все его подмножества.
2. Множество , содержащее по одному элементу: {a} , {b} , {c} .
3. Множество, содержащее два элемента: {a, b} , {b, c} , {a, c} .
4. Множество, содержащее три элемента: {a , b, c} .

Практические задания:
?\? = {1;3;9) ,
б) ?∩? = (2,3) ,
?∪? = [-3, 10] , ?\? = [-32] , ?\A = [3,10]

Практические задания:
3. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия» . Найдите пересечение и объединение множеств А и В.
Решение:
А = {м, а, т, е, и, к} ;
B = {с, т, е, р, о, м, и, я}.
?∩? = {м, т, е, и} ;
?∪? = { м, а, т, е, и, к, с, р, о, я} .

ДЕЙСТВИЯ НАД ЧИСЛАМИ
Сложение. Это действие состоит в том, что по нескольким числам, называемым слагаемыми, находится число, называемое их суммой.
Вычитание – действие, посредством которого по данной сумме (уменьшаемое) и данному слагаемому (вычитаемое) находят искомое слагаемое (разность). Это действие обратно сложению.
Умножение. Умножить некоторое число (множимое) на целое число (множитель) – значит повторить множимое слагаемым столько раз, сколько единиц содержится в множителе. Результат умножения называется произведением.
Деление. Посредством деления по данному произведению (делимое) и данному сомножителю (делитель) находят искомый сомножитель (частное).Это действие обратно умножению.
Возведение в степень. Возвести некоторое число в целую степень (во вторую, в третью и т.д.) – значит взять это число сомножителем два, три раза и т.д. Иначе говоря, возведение в степень выполняется повторным умножением.
Извлечение корня есть действие, посредством которого по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят искомое основание (корень).

ТЕСТ
Перейди по ссылке и пройди тест:

НАТУРАЛЬНЫЕ ЧИСЛА
НАТУРАЛЬНЫЕ ЧИСЛА – ЧИСЛА, ПОЛУЧАЕМЫЕ В РЕЗУЛЬТАТЕ СЧЕТА
ПРОСТЫЕ ЧИСЛА – ЧИСЛА, ДЕЛЮЩИЕСЯ НА САМИХ СЕБЯ И НА ЕДИНИЦУ
ЦЕЛЫЕ ЧИСЛА – ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ НАТУРАЛЬНЫЕ ЧИСЛА

СВОЙСТВА ПРОСТЫХ ЧИСЕЛ
ОБЩИЙ ВИД ПРОСТОГО ЧИСЛА: Р = 2·k + 1, где р - простое число, больше или равное трем.
Два натуральных числа называются взаимно простыми, если они не имеют общих делателей, кроме единицы;
Если взять два взаимно простых числа m и n и если число k делиться на каждое из них, то оно делиться на их произведение (верно и обратное);
Произведение натуральных чисел делится на простое число тогда и только тогда, когда хотя бы одно из них делится на это простое число;
Простых чисел бесконечно много (не существует самого большого простого числа);
Если натуральное число не делится ни на одно простое число, квадрат которого не превосходит это натуральное число, то оно само является простым.

НЕМНОГО О ЦЕЛЫХ ЧИСЕЛ

ПРИЗНАКИ ДЕЛИМОСТИ:
Число делится на 2 тогда и только тогда, когда его последняя цифра является четной, т.е. также делится на два;
Число делится на 3 тогда и только тогда, когда сумма всех его цифр, также, делится на три;
Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре ( ПРИМЕР: 64 – делится на 4, т.к. 6⋅2+4=16, а 16:4=4);
Число делится на 5 тогда и только тогда, когда его последняя цифра – это 0 или 5;
Число делится на 6 тогда и только тогда, когда он одновременно кратно и двум, и трем;
Число делится на 7 тогда и только тогда, когда сумма утроенного числа его десятков и цифры в разряде единиц, также, делится на семь.( ПРИМЕР: 91 – делится на 7, т.к. 9⋅3+1=28, а 28:7=4);
Число делится на 9 тогда и только тогда, когда сумма всех его цифр, также, делится на девять.

ТЕСТ
Перейди по ссылки и пройди тест:

НОД И НОК
НОД ( наибольший общий делитель) есть наибольшее число, делящееся на каждое из данных числе;
НОК ( наименьшее общее кратное) есть наименьшее число, делящееся на каждое из данных чисел.
Для нахождения НОД требуется разложить несколько представленных числе на множители простых множители и найти произведение общих множителей из разложенных этих чисел. А для определения НОК требуется разложить представленные числа на простые множители и найти произведение большего числа на множители из разложения меньшего числа, которых нет в разложении большего числа.

РАЦИОНАЛЬНЫЕ ЧИСЛА

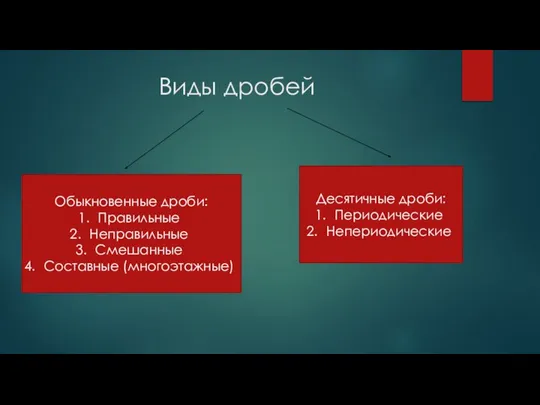
Виды дробей
Обыкновенные дроби:
Правильные
Неправильные
Смешанные
Составные (многоэтажные)
Десятичные дроби:
Периодические
Непериодические

ИРРАЦИОНАЛЬНЫЕ ЧИСЛА
ИРРАЦИОНАЛЬНЫЕ - числа, которые не является рациональным, то есть не может быть представлено в виде обыкновенной дроби может быть представлено в виде бесконечной непериодической десятичной дроби.

Практическое задание:
Для того, чтобы дробь была равна целому числу нужно, чтобы знаменатель ??+? имел n = -9,-1,1

СРЕДНИЕ ВЕЛИЧИНЫ

Абсолютная величина (модуль)
Модулем или абсолютной величиной действительного числа называют:
Само число, если оно положительное ;
Ноль (нуль), если число равно нулю;
Минус число, если оно отрицательное

Свойства модуля
Геометрический смысл:
«расстояние на координатной прямой от начала отсчёта до точки, обозначающей соответствующее число»

Отношения, пропорции и проценты
Прямо пропорциональная зависимость: линейное изменение величин
Обратно пропорциональная зависимость: нелинейное изменение величин

Практические задания:
1. Из 20 тонн руды выплавляют 10 тонн металла, содержащего 80% примесей. Определите процент примесей в руде.

Практические задания:
2. Найдите число, если известно, что 55,5 составляет 18,75% этого числа.
Решение:
Пусть x – неизвестное число.

АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ