Содержание
- 2. Постморфологический анализ =предсинтаксический анализ Предназначен для устранения морфологической омонимии (многозначности) слов Выбор правильной леммы Уточнение морфологических
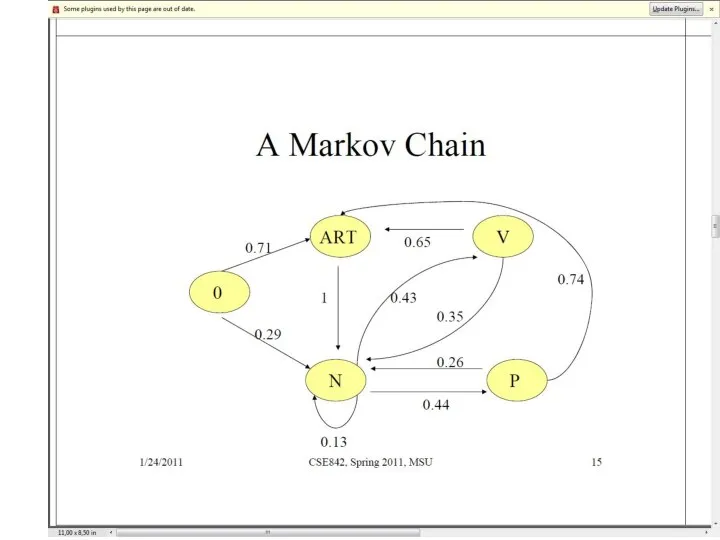
- 3. Набор состояний: Процесс движется от одного состояния к другому, порождая последовательность состояний : Свойство марковской цепи:
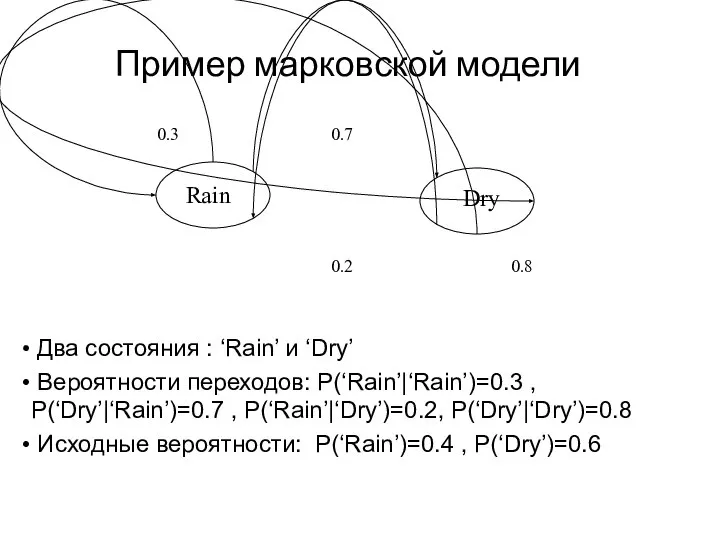
- 4. Два состояния : ‘Rain’ и ‘Dry’ Вероятности переходов: P(‘Rain’|‘Rain’)=0.3 , P(‘Dry’|‘Rain’)=0.7 , P(‘Rain’|‘Dry’)=0.2, P(‘Dry’|‘Dry’)=0.8 Исходные вероятности:
- 5. По свойству марковской цепи, вероятность последовательности состояний может быть найдена по формуле Предположим, мы хотим подсчитать
- 6. Скрытые марковские модели Множество состояний: Процесс движется от состояния к состоянию : Выполняется свойство марковской цепи:
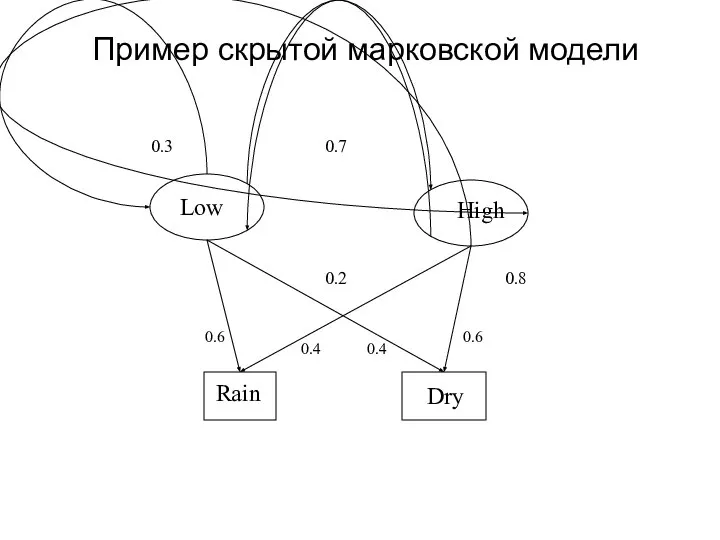
- 7. Dry 0.6 0.6 0.4 0.4 Пример скрытой марковской модели
- 8. Два состояния: ‘Низкое’ and ‘Высокое’ атм. давление. Два наблюдения: ‘Дождь’ and ‘Сухо’. Вероятности перехода: P(‘Low’|‘Low’)=0.3 ,
- 9. Хотим вычислить вероятность последовательности, {‘Dry’,’Rain’}. Рассмотрим все возможные скрытые состояния: P({‘Dry’,’Rain’} ) = P({‘Dry’,’Rain’} , {‘Low’,’Low’})
- 10. Почему важно рассмотрение HMM в автоматической обработке текста Непосредственно имеем дело с неоднозначными словами и конструкциями
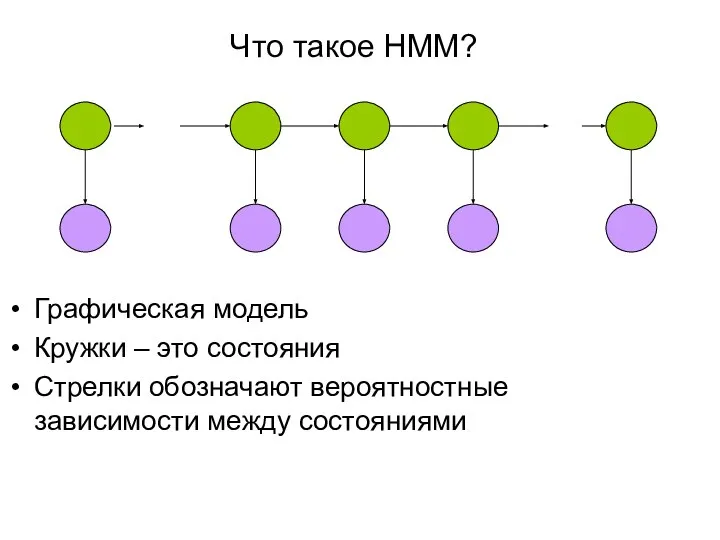
- 11. Что такое HMM? Графическая модель Кружки – это состояния Стрелки обозначают вероятностные зависимости между состояниями
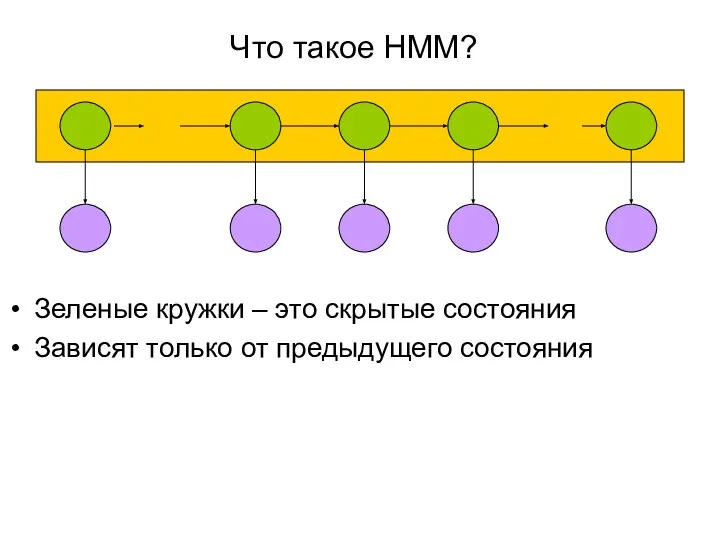
- 12. Что такое HMM? Зеленые кружки – это скрытые состояния Зависят только от предыдущего состояния
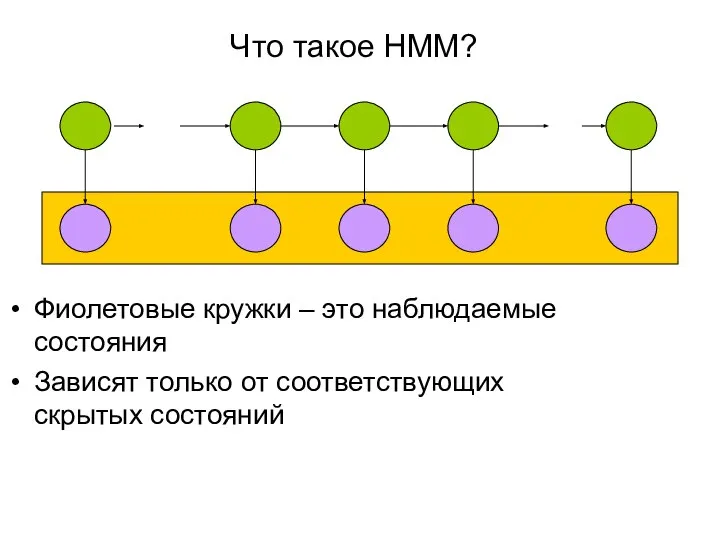
- 13. Что такое HMM? Фиолетовые кружки – это наблюдаемые состояния Зависят только от соответствующих скрытых состояний
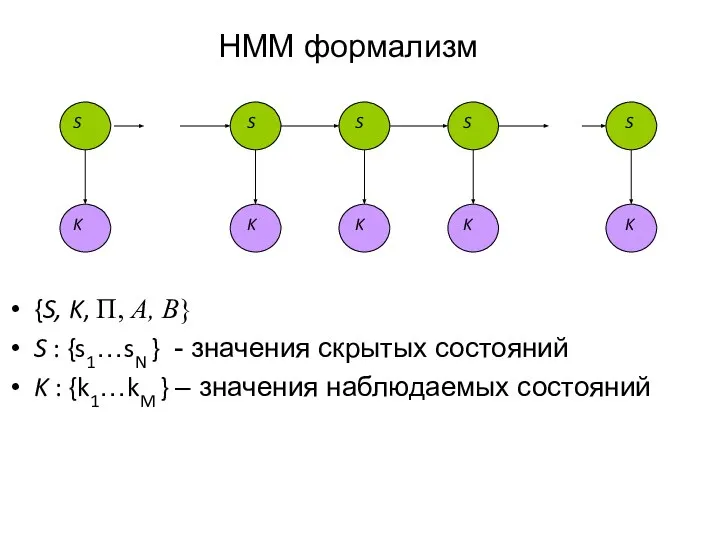
- 14. HMM формализм {S, K, Π, Α, Β} S : {s1…sN } - значения скрытых состояний K
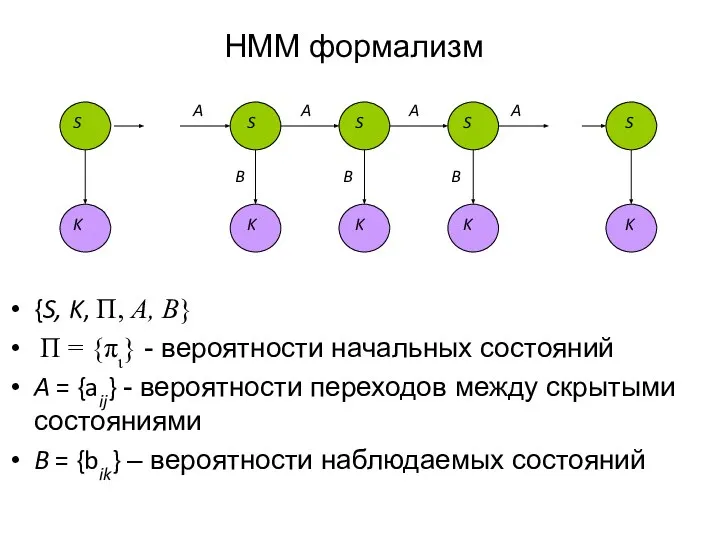
- 15. HMM формализм {S, K, Π, Α, Β} Π = {πι} - вероятности начальных состояний A =
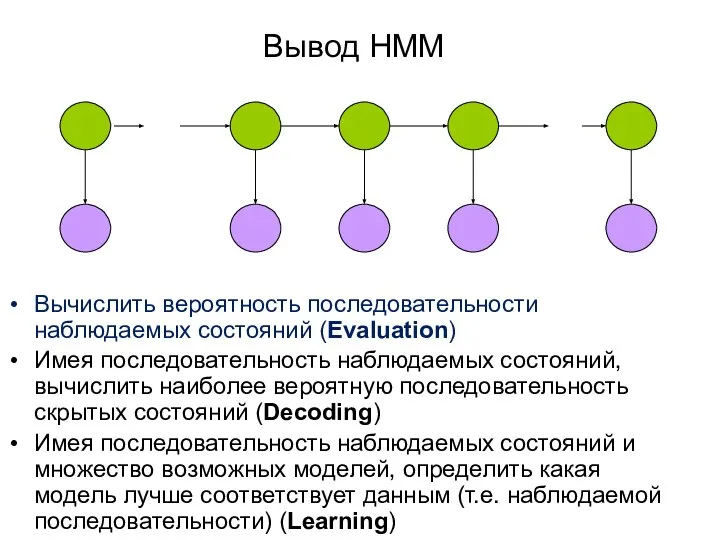
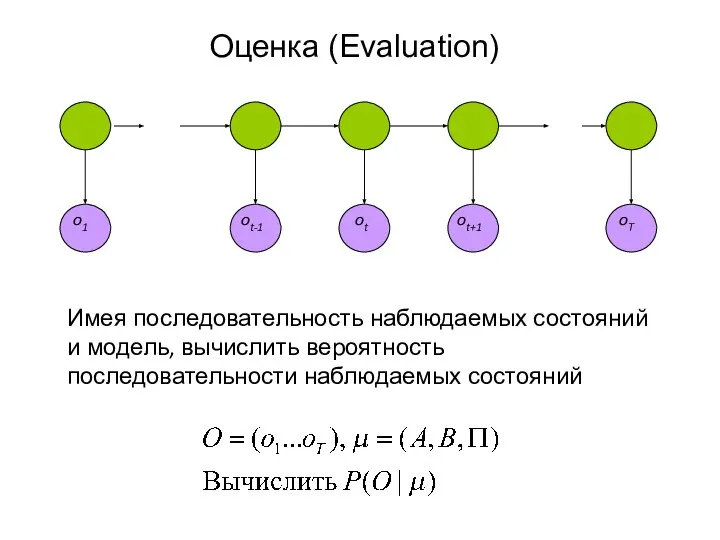
- 16. Вывод HMM Вычислить вероятность последовательности наблюдаемых состояний (Evaluation) Имея последовательность наблюдаемых состояний, вычислить наиболее вероятную последовательность
- 17. o1 ot ot-1 ot+1 Имея последовательность наблюдаемых состояний и модель, вычислить вероятность последовательности наблюдаемых состояний Оценка
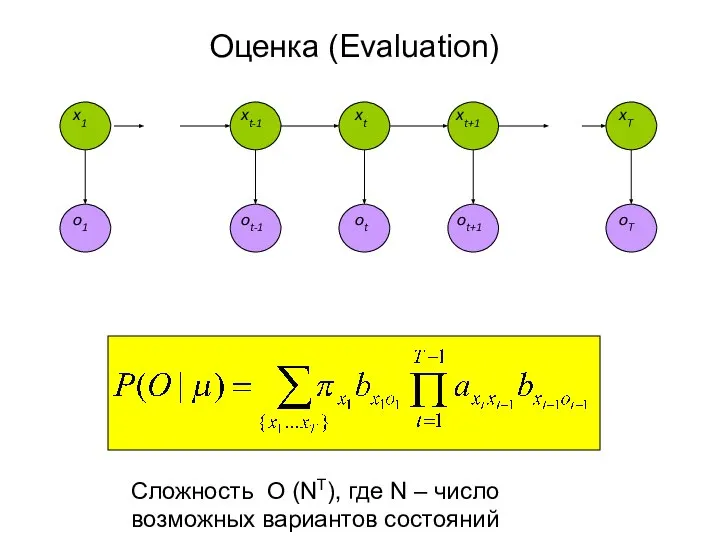
- 18. Оценка (Evaluation) Сложность O (NT), где N – число возможных вариантов состояний
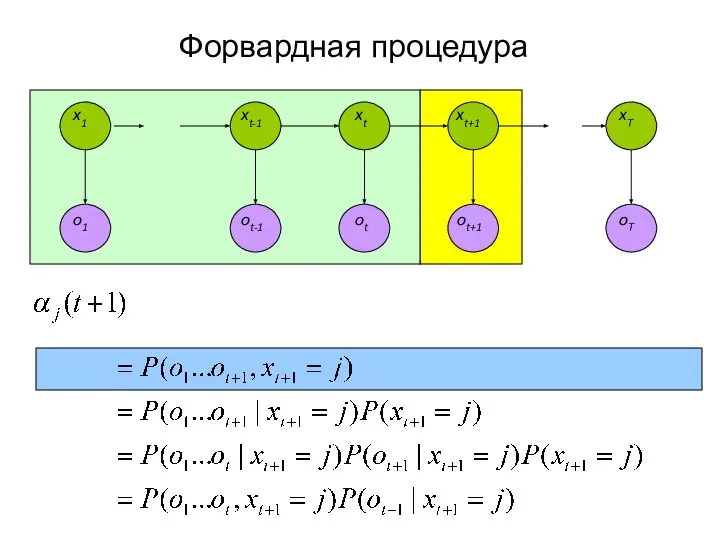
- 19. Форвардная процедура Метод динамического программирования Определим переменную: Смысл переменной α: вероятность наблюдений o1, …ot и при
- 20. Форвардная процедура
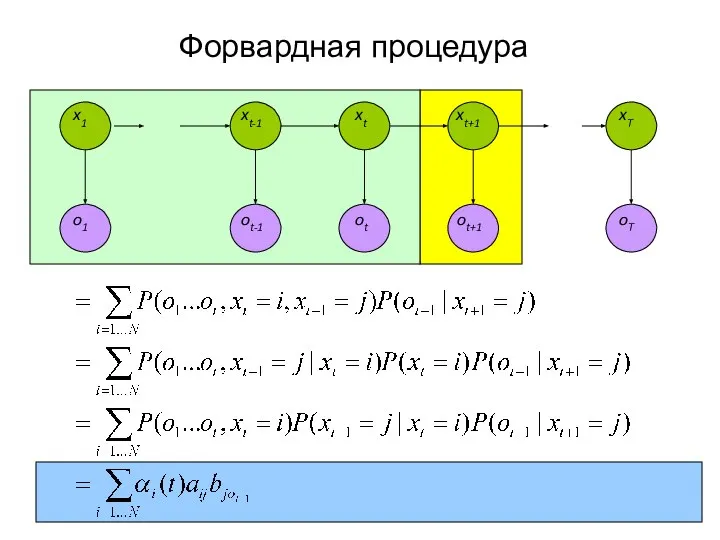
- 21. Форвардная процедура
- 22. Вычисление вероятности последовательности наблюдаемых событий Можем эффективно вычислять αT(I)=P(o1, o2,…oT, xT=i|μ) Как вычислить P(o1, o2,…oT |μ)?
- 23. Вычисление вероятности последовательности наблюдаемых событий Можем эффективно вычислять αT(i)=P(o1, o2,…oT, xT=i|μ) Как вычислить P(o1, o2,…oT |μ)
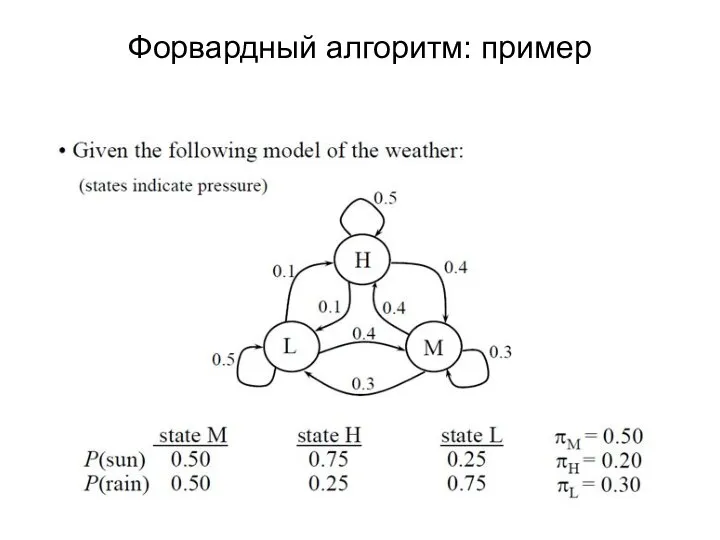
- 24. Форвардный алгоритм: пример
- 25. Форвардный алгоритм Найти вероятность последовательности: s r r s r (s- sun, r – rain)
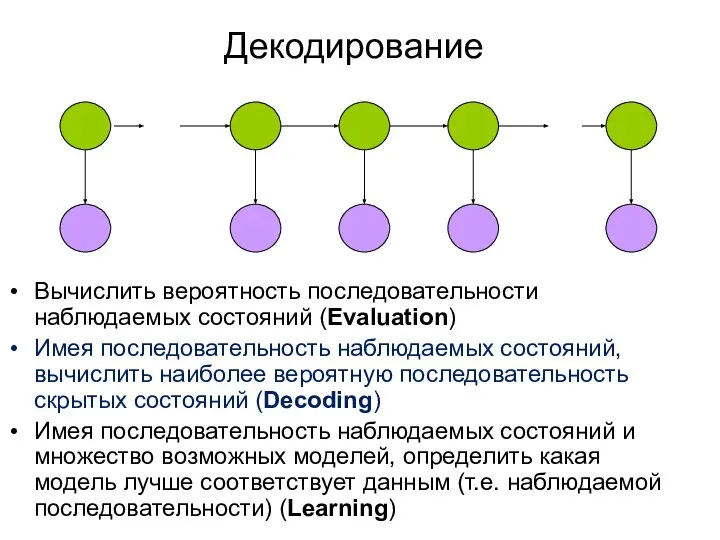
- 28. Декодирование Вычислить вероятность последовательности наблюдаемых состояний (Evaluation) Имея последовательность наблюдаемых состояний, вычислить наиболее вероятную последовательность скрытых
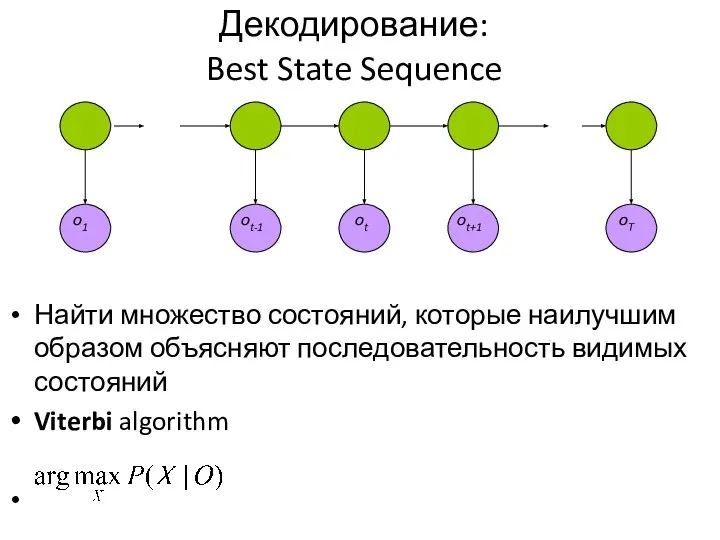
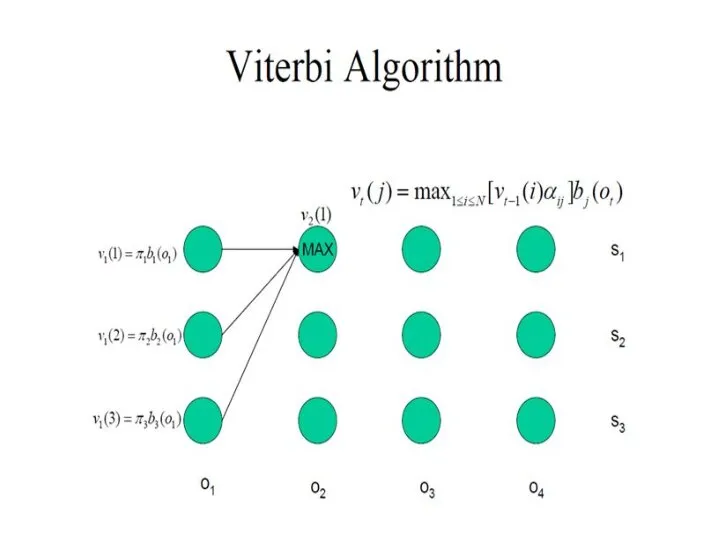
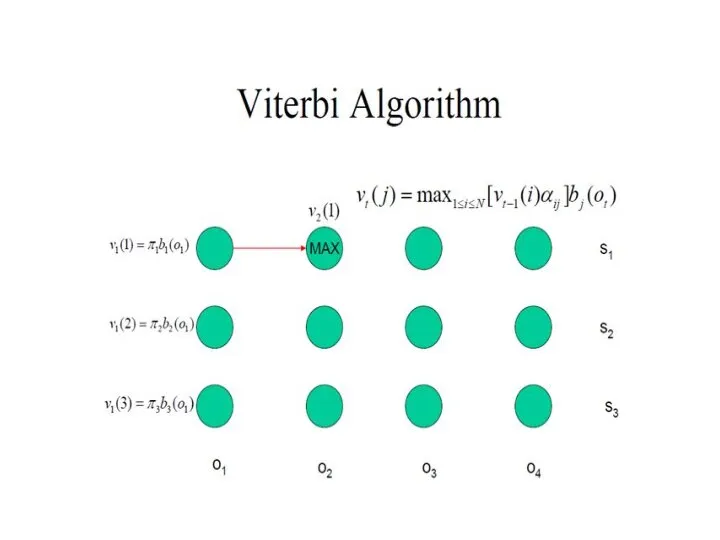
- 29. Декодирование: Best State Sequence Найти множество состояний, которые наилучшим образом объясняют последовательность видимых состояний Viterbi algorithm
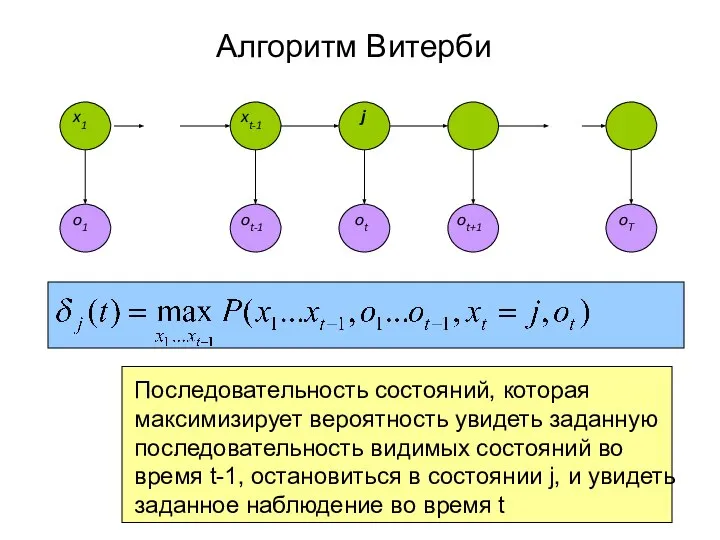
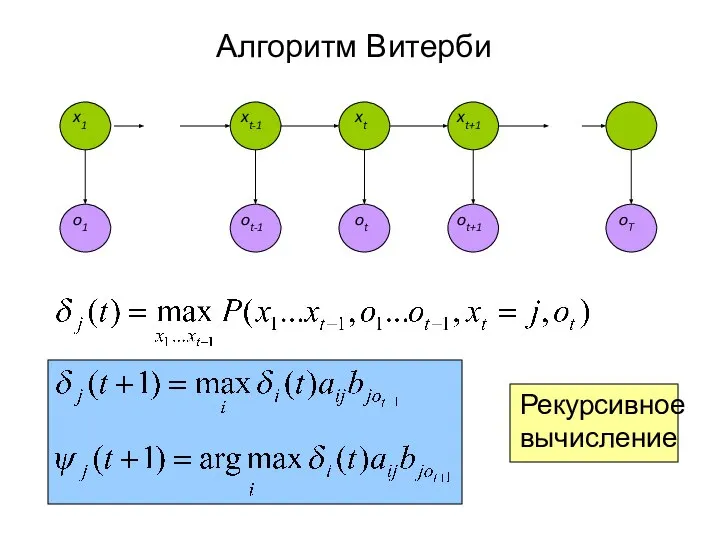
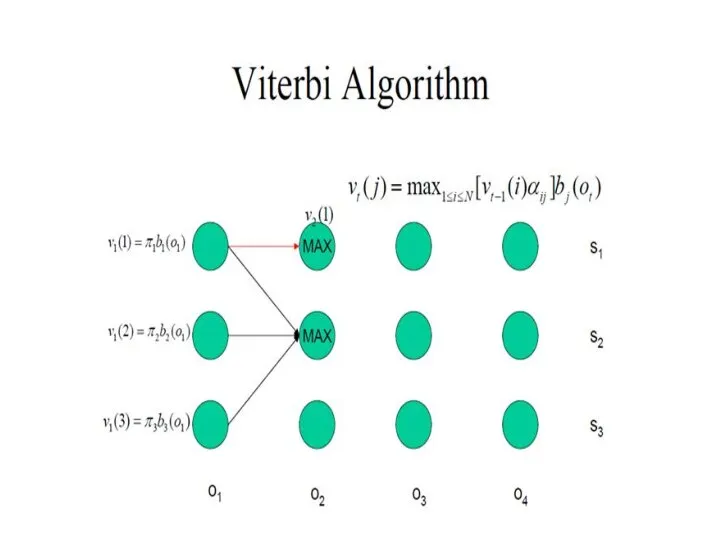
- 30. oT o1 ot ot-1 ot+1 Алгоритм Витерби Последовательность состояний, которая максимизирует вероятность увидеть заданную последовательность видимых
- 31. Алгоритм Витерби Рекурсивное вычисление x1 xt-1 xt xt+1
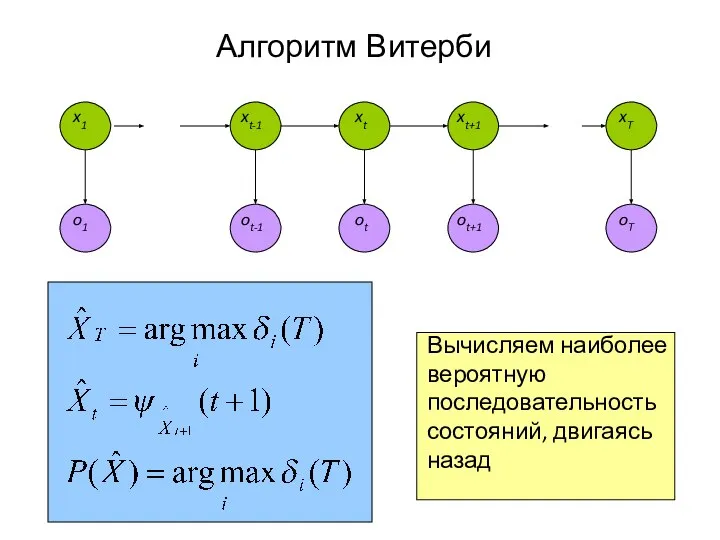
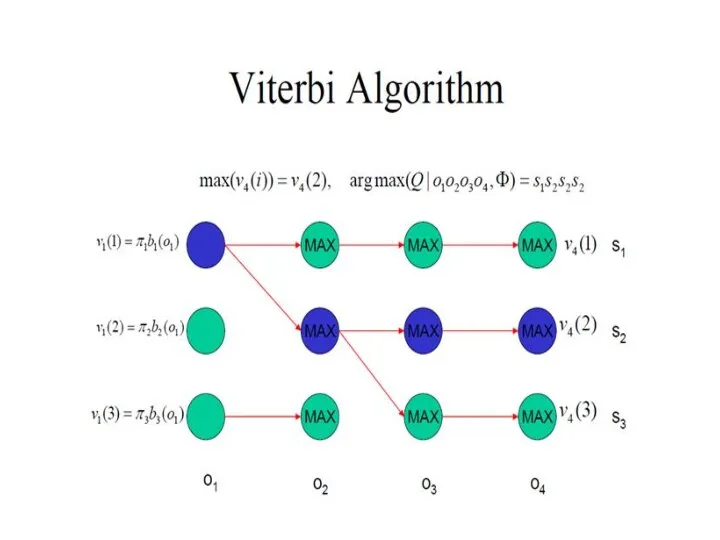
- 32. Алгоритм Витерби Вычисляем наиболее вероятную последовательность состояний, двигаясь назад x1 xt-1 xt xt+1 xT
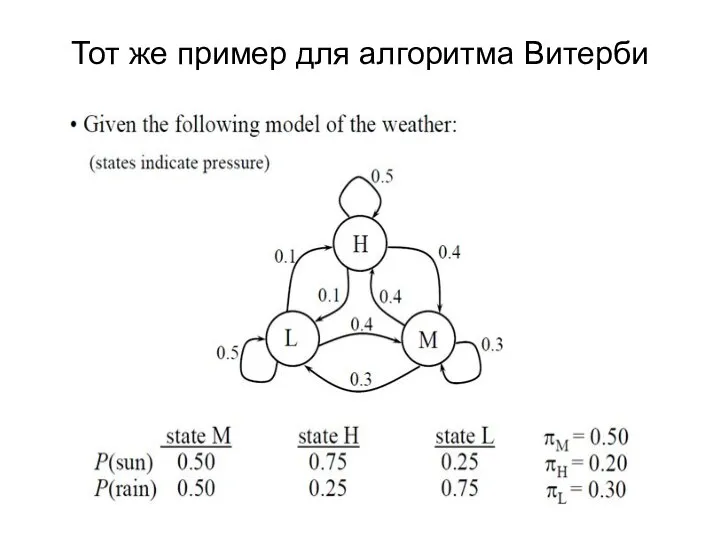
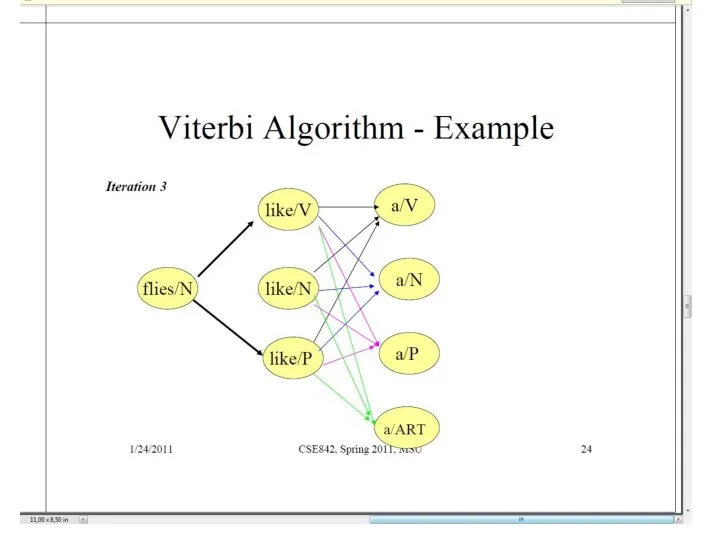
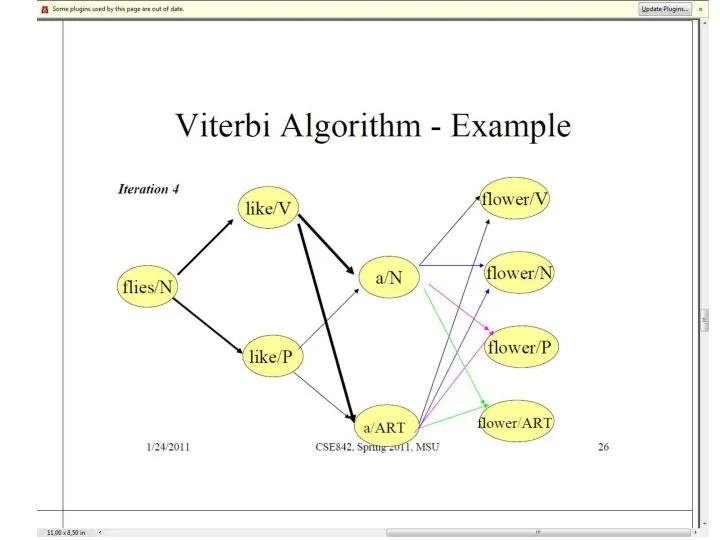
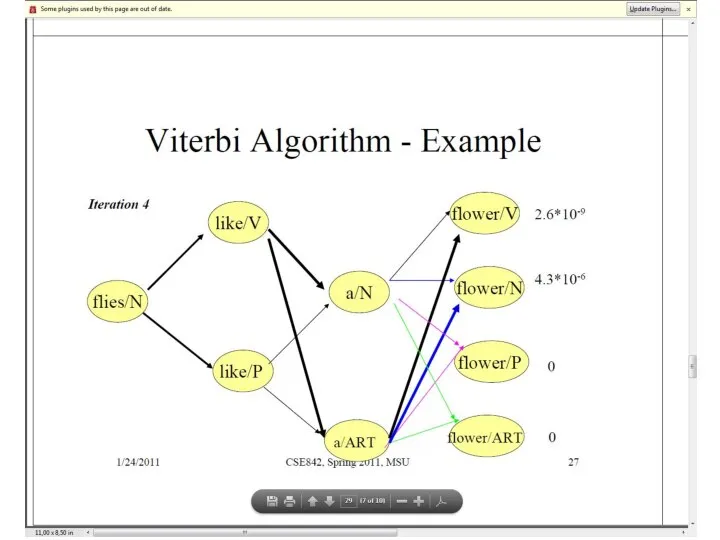
- 39. Тот же пример для алгоритма Витерби
- 40. Пример: Алгоритм Витерби
- 41. Пример. Алгоритм Витерби
- 42. Применение HMM к POS-tagging POS-tagging – морфологическая разметка HMM tagger: выбирает наиболее вероятную последовательность тегов для
- 43. Пример: морфологическая неоднозначность
- 44. Откуда взять данные? Из корпуса с морфологической разметкой Русский язык: Корпус русского языка Открытый корпус (opencorpora.org)
- 45. Фрагмент морфологической разметки в Национальном корпусе русского языка Я сидел на барском сиденье, дышал горячим ветром,
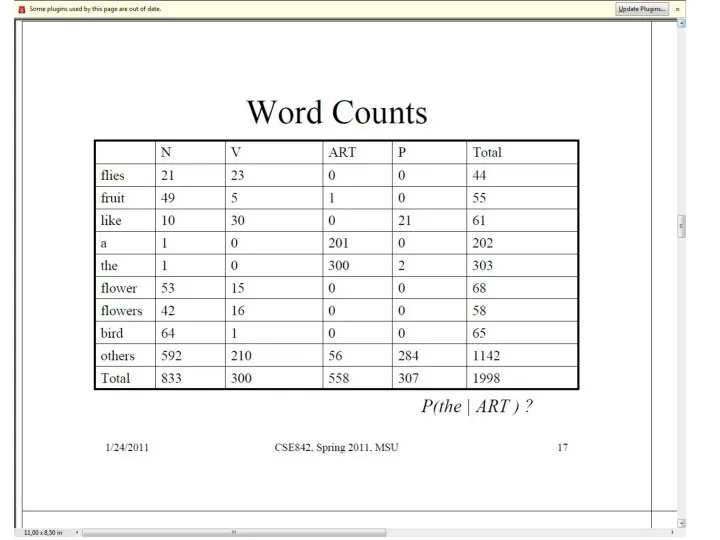
- 46. Данные для примера
- 59. Лексические вероятности: уточнение Мы считали p(w|t) Но Слово могло отсутствовать в корпусе или отсутствовать в заданной
- 60. Лексические вероятности ~ p(t) – априорная вероятность метки p(t|w) – вероятность метки для данного слова Можно
- 61. Словарь и лексические вероятности Можно считать, что все словарные метки слова w входят в корпус α
- 62. Анализ статистических алгоритмов снятия морфологической омонимии в русском языке Егор Лакомкин Иван Пузыревский Дарья Рыжова (2013)
- 63. Разрешение морфологической неоднозначности в текстах на английском языке Методы: Как правило, статистические алгоритмы на основе марковских
- 64. Особенности английского языка Бедная морфология морфологическая разметка фактически сводится к POS-теггингу Фиксированный порядок слов можно опираться
- 65. Задача исследования: Проверить экспериментально, применимы ли статистические алгоритмы, основанные на марковских моделях, к задаче морфологической дизамбигуации
- 66. Алгоритмы Набор скрытых величин Y (состояний модели = наборов грамматических тегов); составляют марковскую цепь первого порядка
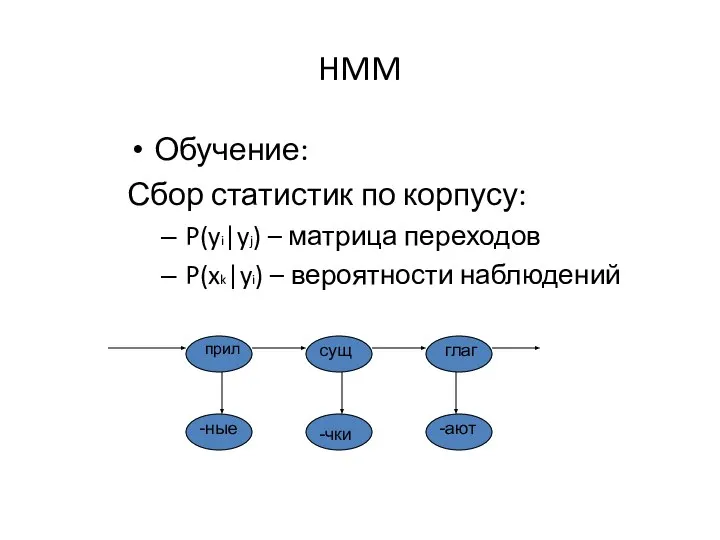
- 67. HMM Обучение: Сбор статистик по корпусу: P(yi|yj) – матрица переходов P(xk|yi) – вероятности наблюдений сущ прил
- 68. Задача алгоритмов: Вычисление наиболее вероятной последовательности скрытых величин
- 69. Деление выборки на обучающую и тестирующую: Кросс-валидация (5 фолдов): Деление выборки на 5 частей: 4 обучающие
- 70. Оценка качества Определение верхней и нижней границы: Верхняя граница: процент случаев, когда среди гипотез Mystem’а есть
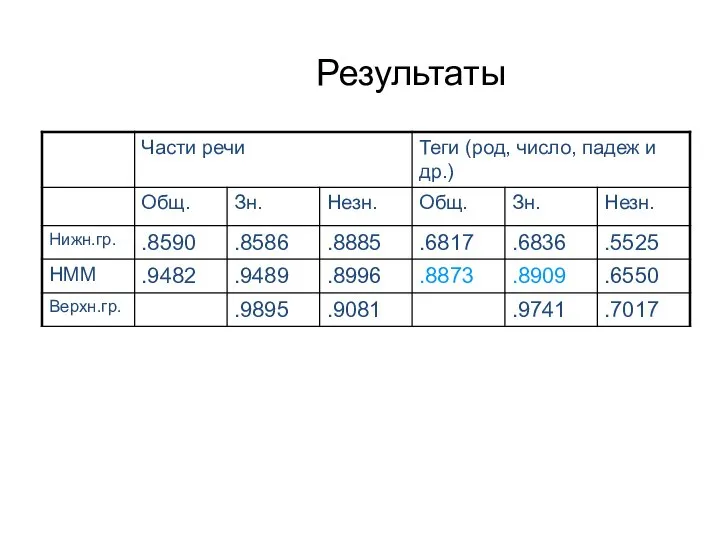
- 71. Результаты
- 72. Выводы работы POS-теггинг – на приличном уровне, Разрешение неоднозначности по расширенным тегам – довольно низкий уровень
- 73. Проблемы HMM Метки рассматриваются как единое целое, невозможно извлечь отдельные признаки В русском языке: тег –
- 74. Как можно изменить процесс расчета переходов между состояниями? HMM: учитываются два фактора в простой комбинации Для
- 76. Скачать презентацию











































 Отдел мхи
Отдел мхи Курица. Кулинарные рецепты
Курица. Кулинарные рецепты Рекомендации по разработке и оформлению дополнительных общеобразовательных программ, город Ульяновск
Рекомендации по разработке и оформлению дополнительных общеобразовательных программ, город Ульяновск IFC Advisory Services Проект развития первичного рынка ипотеки в РоссииКонференция АК&М
IFC Advisory Services Проект развития первичного рынка ипотеки в РоссииКонференция АК&М Профессиограмма директора школы
Профессиограмма директора школы Строим город. ИЗО
Строим город. ИЗО Общая характеристика гражданского, семейного, трудового законодательства
Общая характеристика гражданского, семейного, трудового законодательства Искусство кукольного театра
Искусство кукольного театра Культура России первой половины XIX века
Культура России первой половины XIX века Solutions
Solutions L'arrivee des couleurs
L'arrivee des couleurs Royal Britain
Royal Britain lightning
lightning  Мастер класс Мой первый кулинарный опыт. Салат Витаминный
Мастер класс Мой первый кулинарный опыт. Салат Витаминный ВВОДНАЯ ЛЕКЦИЯ ПО ТЕМЕ. Основы формирования жилищной сферы в Российской Федерации Преподаватели:
ВВОДНАЯ ЛЕКЦИЯ ПО ТЕМЕ. Основы формирования жилищной сферы в Российской Федерации Преподаватели: Организация производственного процесса в холодном цехе
Организация производственного процесса в холодном цехе Схема установки и принцип работы встроенного таймера электричества
Схема установки и принцип работы встроенного таймера электричества Культура как объект культурологии. История понятия Культура
Культура как объект культурологии. История понятия Культура Виды искусств
Виды искусств Русский язык. Анализ текста (уровень C)
Русский язык. Анализ текста (уровень C) Презентация на тему Серная кислота
Презентация на тему Серная кислота Готическая архитектура. Миланский собор
Готическая архитектура. Миланский собор Coca-Cola
Coca-Cola Geotermalnaya_elektrostantsia (1)
Geotermalnaya_elektrostantsia (1) Образовательные технологии на уроках истории
Образовательные технологии на уроках истории Презентация на тему ШКАЛА ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ
Презентация на тему ШКАЛА ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ  Табличное представление данных
Табличное представление данных  Can you tell me the way to the zoo, please
Can you tell me the way to the zoo, please