ДИФРАКЦИОННАЯ КОМПЬЮТЕРНАЯ ОПТИКА

СОДЕРЖАНИЕ
2
Введение
Часть I. Основы дифракционной
компьютерной оптики (ДКО)
Дифракционные оптические элементы (ДОЭ)
Компенсаторы волнового фронта
Фокусаторы лазерного излучения
Компьютерный синтез ДОЭ
Селекция мод лазерного излучения
Бессель-оптика и вихревые лазерные пучки
Решение уравнений Максвелла
Часть II. ДКО и нанофотоника
Оптический захват и микроманипулирование
Фотонно-кристаллические структуры
Управление магнитооптическими гетеронаноструктурами
Часть III. Дифракционные гетероструктуры в наноплазмонике
Формирование интерференционных
картин поверхностных электромагнитных
волн (ПЭВ)
Фокусировка ПЭВ с помощью ДОЭ
Заключение
А.М. Прохоров
(1916-2002)
И.Н. Сисакян
(1938-1995)

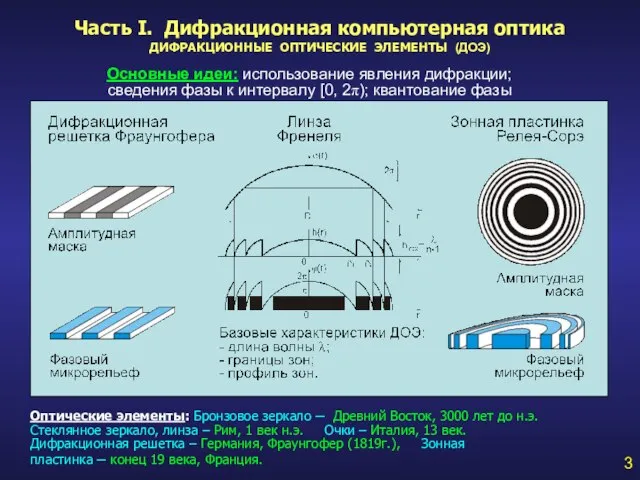
Часть I. Дифракционная компьютерная оптика
ДИФРАКЦИОННЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ (ДОЭ)
3
Основные идеи: использование явления дифракции; сведения фазы к интервалу [0, 2π); квантование фазы
Оптические элементы: Бронзовое зеркало – Древний Восток, 3000 лет до н.э.
Стеклянное зеркало, линза – Рим, 1 век н.э. Очки – Италия, 13 век.
Дифракционная решетка – Германия, Фраунгофер (1819г.), Зонная
пластинка – конец 19 века, Франция.

М.А. Голуб, Е.С. Живописцев, С.В. Карпеев, А.М. Прохоров, И.Н. Сисакян, В.А. Сойфер <Получение асферических волновых фронтов при помощи машинных голограмм>, Доклады АН СССР, т.253,№ 5, с.1104-1108 (август, 1980).
КОМПЕНСАТОРЫ ВОЛНОВОГО ФРОНТА –
ПЕРВЫЕ ЭЛЕМЕНТЫ ДКО
Фотошаблон компенсатора
«сфера - внеосевой сегмент параболоида»
Фотошаблон компенсатора «сфера-параболоид»
4
Оптическая схема для тестирования
асферических зеркал
Требуемая точность контроля асферических зеркал λ/50- λ/100, а достижимая технологически на сегодня
точность изготовления дифракционных компенсаторов
не лучше λ/10. Это ограничивает их применение.

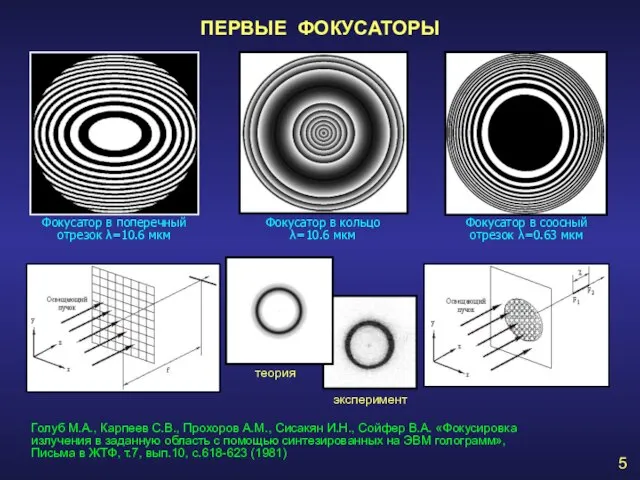
ПЕРВЫЕ ФОКУСАТОРЫ
Фокусатор в поперечный
отрезок λ=10.6 мкм
Фокусатор в кольцо λ=10.6 мкм
Фокусатор в соосный
отрезок λ=0.63 мкм
5
Голуб М.А., Карпеев С.В., Прохоров А.М., Сисакян И.Н., Сойфер В.А. «Фокусировка излучения в заданную область с помощью синтезированных на ЭВМ голограмм»,
Письма в ЖТФ, т.7, вып.10, с.618-623 (1981)
эксперимент
теория

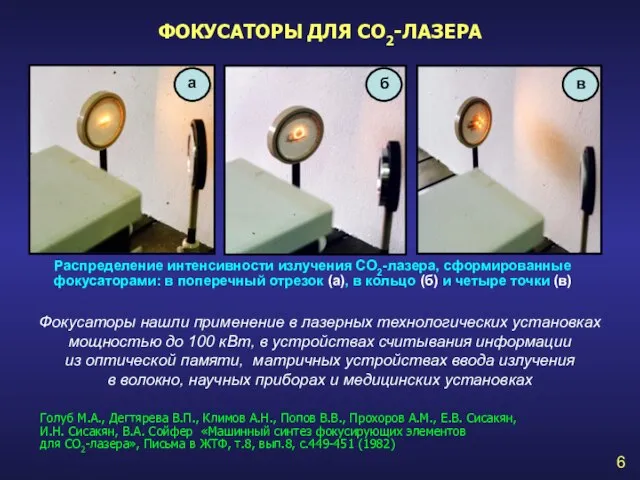
ФОКУСАТОРЫ ДЛЯ CO2-ЛАЗЕРА
Распределение интенсивности излучения СО2-лазера, сформированные
фокусаторами: в поперечный отрезок (а), в кольцо (б) и четыре точки (в)
Фокусаторы нашли применение в лазерных технологических установках
мощностью до 100 кВт, в устройствах считывания информации
из оптической памяти, матричных устройствах ввода излучения
в волокно, научных приборах и медицинских установках
6
Голуб М.А., Дегтярева В.П., Климов А.Н., Попов В.В., Прохоров А.М., Е.В. Сисакян,
И.Н. Сисакян, В.А. Сойфер «Машинный синтез фокусирующих элементов
для СО2-лазера», Письма в ЖТФ, т.8, вып.8, с.449-451 (1982)

7
ФОКУСАТОРЫ НА АЛМАЗНЫХ ПЛЕНКАХ
Длина волны: λ = 10,6 мкм
Мощность: 2.1 kВт
Фокальная область: точка, отрезок, кольцо
Энергетическая
эффективность: 90%
Фрагменты рельефа
фокусатора
Показатель преломления пленки = 2,4; толщина пленки = 1 мм
Конов В.И., Прохоров A.M.,
Павельев В.С., Сойфер В.А.
Квант. электр., 29(1)9-10(1999)
Расчет параметров субволно-
вого микрорельефа выполнял-
ся с помощью решения урав-
нений Максвелла

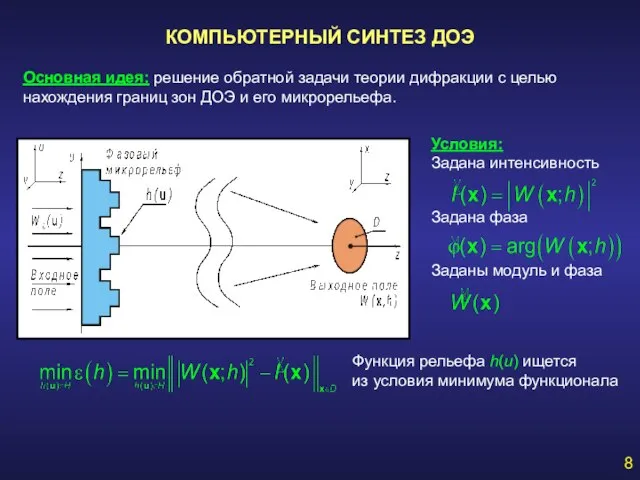
КОМПЬЮТЕРНЫЙ СИНТЕЗ ДОЭ
8
Основная идея: решение обратной задачи теории дифракции с целью нахождения границ зон ДОЭ и его микрорельефа.
Заданы модуль и фаза
Функция рельефа h(u) ищется
из условия минимума функционала
Условия:
Задана интенсивность
Задана фаза

АЛГОРИТМЫ РАСЧЕТА ДОЭ
9
Методы цифровой голографии: кодирование амплитудно фазовой функции с помощью фазовой функции.
(J.P. Kirk, A.L. Jones, J. Opt. Soc. Am. 61(8) 1023 (1971))
Итеративные алгоритмы расчета ДОЭ,
связанные с минимизацией целевых функций.
Присутствует эффект стагнации.
(R.W. Gerchberg, W.O. Saxton, Optik 35 (1972),
237-242)
Градиентные алгоритмы оптимизации
для расчета фазы ДОЭ. Могут быть
использованы и в строгой теории дифракции.
(V. Soifer, V. Kotlyar, L. Doskolovich “Iterative methods for diffractive optical elements computation, Taylor & Francis, London, 1997)
Интерактивная оптимизация: 80% эффективность, 4% ошибка
Схема итеративного
алгоритма Герчберга-Секстона
W0 - амплитуда освещающего пучка, T – комплексная функция пропускания ДОЭ,
I0 – заданное распределение интенсивности в выходной плоскости, A , φ – амплитуда и фаза
в выходной плоскости, рассчитанные на n-ой итерации, B , ψ - амплитуда и фаза в плоскости ДОЭ,
рассчитанные на n-ой итерации, F – комплексная амплитуда в выходной плоскости

ИТЕРАТИВНЫЙ РАСЧЕТ БИНАРНЫХ
И КВАНТОВАННЫХ ДОЭ, ФОКУСИРУЮЩИХ СВЕТ
В ЗАДАННЫЕ ОБЛАСТИ
Бинарные ДОЭ легко изготавливаются с помощью технологии оптической фотолитографии, имеют высокую дифракционную эффективность(~75%)
и небольшую ошибку (1-5 %).
Бинарная фаза ДОЭ, фокусирующего в кольцо
Бинарная фаза ДОЭ, фокусирующего в букву Н
Бинарная фаза одного
периода решетки
с 33x33 порядками
4-х уровневая фаза ДОЭ,
фокусирующего в букву "F"
Распределения интенсивности в фокальной плоскости
10
Methods for Computer Design of Diffractive Optical Elements,
edited by V. Soifer (John Wiley & Sons, New York, 2002)
η=73%
δ=3%
η=75%
δ=5%
η=70%
δ=2%

ТЕХНОЛОГИИ СОЗДАНИЯ ДОЭ
11
Измерение параметров микрорельефа
Технологические
этапы синтеза ДОЭ
Совмещение
Травление
микрорельефа
Формирование защитного покрытия
Вычисление и запись фотомаски
Исследование качества материалов и подложек
Генератор изображений
Leica LION LV1 (разре-
шение 40 нм, изображе-
ние 10х10мм)
Электронный микроскоп
«Supra 25» с литогра-
фической приставкой XENOS (разрешение 100 нм, изображение 0,5х0,5 мм)
CLWS-200 (разрешение 800 нм, изображение 2000х200мм)
Оптическая
литография
Оптический
генератор
изображений
Электронно-лучевая
литография

АВТОМАТИЧЕСКИЙ КОНТРОЛЬ РЕЛЬЕФА ДОЭ
12
А – автоматический интерферометр NewView-5000 фирмы Zygo (США)
способный визуализировать рельеф ДОЭ диаметром 200 мм х 200 мм с поперечным разрешением 1 мкм и с разрешением по высоте 1 нм.
В – бинарная дифракционная решетка на торце многомодового волокна и профиль рельефа ее небольшого участка. Период решетки – 60 мкм, диаметр волокна – 1000 мкм.
В
А

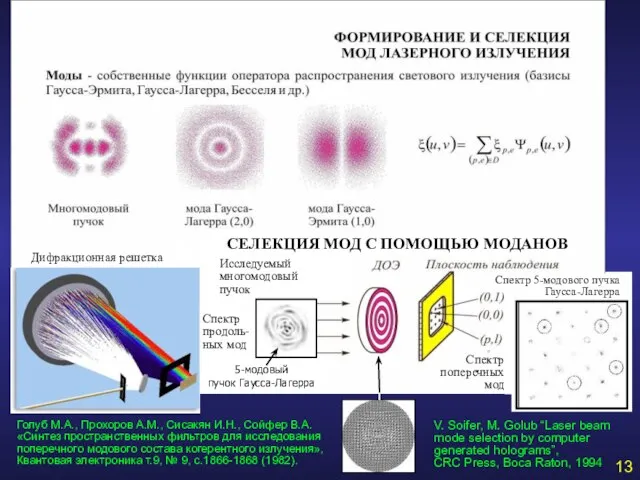
13
Дифракционная решетка
White light
Спектр
продоль-
ных мод
Голуб М.А., Прохоров А.М., Сисакян И.Н., Сойфер В.А. «Синтез пространственных фильтров для исследования поперечного модового состава когерентного излучения», Квантовая электроника т.9, № 9, с.1866-1868 (1982).
СЕЛЕКЦИЯ МОД С ПОМОЩЬЮ МОДАНОВ
V. Soifer, M. Golub “Laser beam
mode selection by computer
generated holograms”,
CRC Press, Boca Raton, 1994
Исследуемый
многомодовый
пучок
Спектр
поперечных
мод
5-модовый
пучок Гаусса-Лагерра
Спектр 5-модового пучка Гаусса-Лагерра

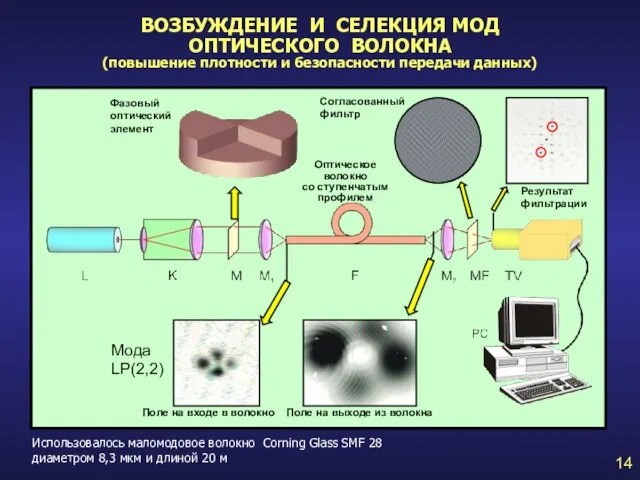
ВОЗБУЖДЕНИЕ И СЕЛЕКЦИЯ МОД
ОПТИЧЕСКОГО ВОЛОКНА
(повышение плотности и безопасности передачи данных)
14
Использовалось маломодовое волокно Corning Glass SMF 28
диаметром 8,3 мкм и длиной 20 м
Мода
LP(2,2)

БЕССЕЛЬ-ОПТИКА И СИНГУЛЯРНАЯ ОПТИКА
Винтовой фазовый ДОЭ
Винтовая
зонная пластина
Березный А.Е., Прохоров А.М., Сисакян И.Н., Сойфер В.А. Бессель-оптика // ДАН, 1984.
Khonina S.N., Kotlyar V.V., Shinkaryev M.V., Soifer V.A., Uspleniev G.V.,
The phase rotor filter
// J. Modern Optics, 1992
Решетка
с «вилкой»
Heckenberg N.R. et al. Generation of optical phase singularities by computer-generated holograms
// Opt. Lett., 1992
Bazhenov V.Yu., Soskin M.S., Vasnetsov M.V. Screw dislocations
in light wavefronts
// J. of Mod. Opt., 1992
m=1
15
- функция фазы терпит m разрывов первого рода, m – порядок ДОЭ

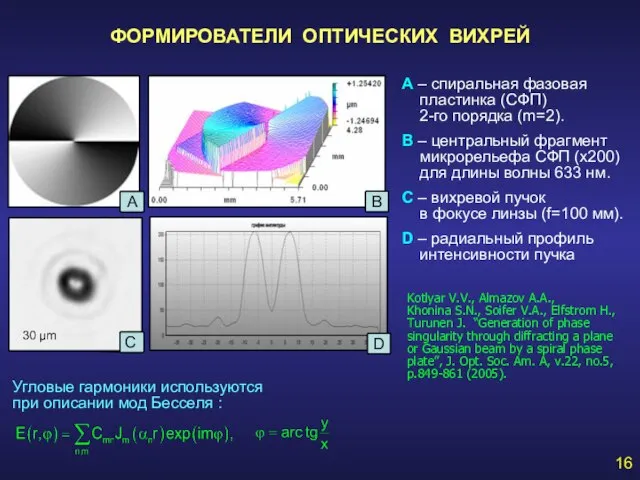
16
ФОРМИРОВАТЕЛИ ОПТИЧЕСКИХ ВИХРЕЙ
А – спиральная фазовая пластинка (СФП) 2-го порядка (m=2).
В – центральный фрагмент микрорельефа СФП (х200)
для длины волны 633 нм.
С – вихревой пучок
в фокусе линзы (f=100 мм).
D – радиальный профиль интенсивности пучка
Угловые гармоники используются
при описании мод Бесселя :
Kotlyar V.V., Almazov A.A.,
Khonina S.N., Soifer V.A., Elfstrom H.,
Turunen J. “Generation of phase
singularity through diffracting a plane
or Gaussian beam by a spiral phase
plate”, J. Opt. Soc. Am. A, v.22, no.5,
p.849-861 (2005).

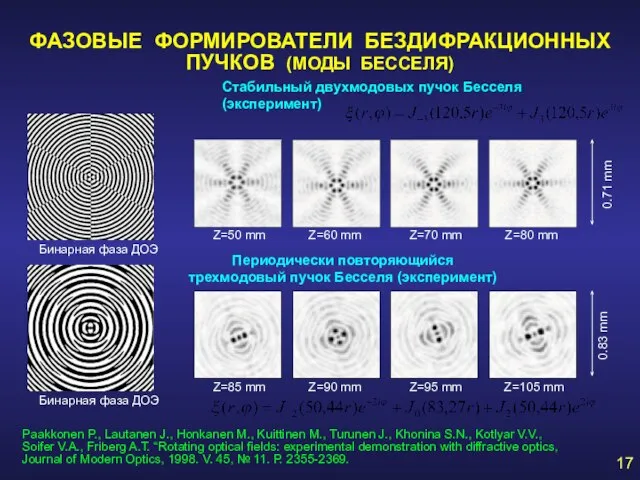
ФАЗОВЫЕ ФОРМИРОВАТЕЛИ БЕЗДИФРАКЦИОННЫХ
ПУЧКОВ (МОДЫ БЕССЕЛЯ)
Стабильный двухмодовых пучок Бесселя
(эксперимент)
Периодически повторяющийся
трехмодовый пучок Бесселя (эксперимент)
Бинарная фаза ДОЭ
Бинарная фаза ДОЭ
Z=50 mm
Z=60 mm
Z=70 mm
Z=80 mm
Z=85 mm
Z=90 mm
Z=95 mm
Z=105 mm
0.71 mm
0.83 mm
17
Paakkonen P., Lautanen J., Honkanen M., Kuittinen M., Turunen J., Khonina S.N., Kotlyar V.V.,
Soifer V.A., Friberg A.T. “Rotating optical fields: experimental demonstration with diffractive optics,
Journal of Modern Optics, 1998. V. 45, № 11. Р. 2355-2369.

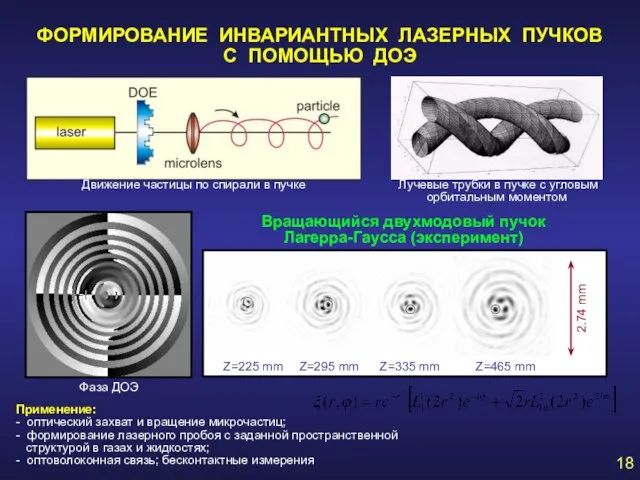
ФОРМИРОВАНИЕ ИНВАРИАНТНЫХ ЛАЗЕРНЫХ ПУЧКОВ
С ПОМОЩЬЮ ДОЭ
Вращающийся двухмодовый пучок
Лагерра-Гаусса (эксперимент)
Применение:
- оптический захват и вращение микрочастиц;
- формирование лазерного пробоя с заданной пространственной структурой в газах и жидкостях;
- оптоволоконная связь; бесконтактные измерения
18
Движение частицы по спирали в пучке Лучевые трубки в пучке с угловым
орбитальным моментом

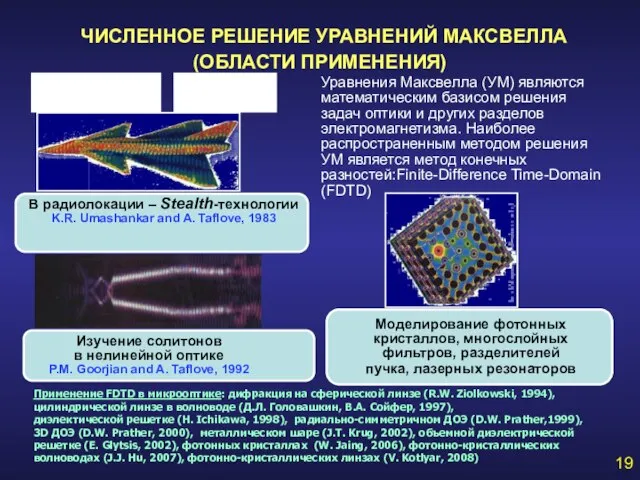
ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ МАКСВЕЛЛА
(ОБЛАСТИ ПРИМЕНЕНИЯ)
19
Изучение солитонов
в нелинейной оптике
P.M. Goorjian and A. Taflove, 1992
Уравнения Максвелла (УМ) являются математическим базисом решения
задач оптики и других разделов электромагнетизма. Наиболее распространенным методом решения УМ является метод конечных разностей:Finite-Difference Time-Domain (FDTD)
Применение FDTD в микрооптике: дифракция на сферической линзе (R.W. Ziolkowski, 1994),
цилиндрической линзе в волноводе (Д.Л. Головашкин, В.А. Сойфер, 1997),
диэлектической решетке (H. Ichikawa, 1998), радиально-симметричном ДОЭ (D.W. Prather,1999),
3D ДОЭ (D.W. Prather, 2000), металлическом шаре (J.T. Krug, 2002), объемной диэлектрической
решетке (E. Glytsis, 2002), фотонных кристаллах (W. Jaing, 2006), фотонно-кристаллических
волноводах (J.J. Hu, 2007), фотонно-кристаллических линзах (V. Kotlyar, 2008)

ПРОГРАММНЫЕ СРЕДСТВА
ДЛЯ РАСЧЕТА И МОДЕЛИРОВАНИЯ ДОЭ
20
“QUICK-DOE” – программные
средства для неитеративного
расчета фазы ДОЭ
“ITER-MODE” –
программные
средства
итеративного
расчета ДОЭ,
формирующих
моды
Лагерра-Гаусса
и Эрмита-Гаусса
Коммерческие программные средства:
Full WAVE 6.0 (RSoft Design, US)
FIMMWAVE 4.6 (Photon Design, Oxford,UK)
OlympiOs 5.2 (Alcatel Optronics, Netherlands)
Позволяют моделировать распространение и дифракцию света с помощью строгого (FDTD-метод) и приближенного (BeamProp-метод) решения уравнений Максвелла
Full WAVE 6.0

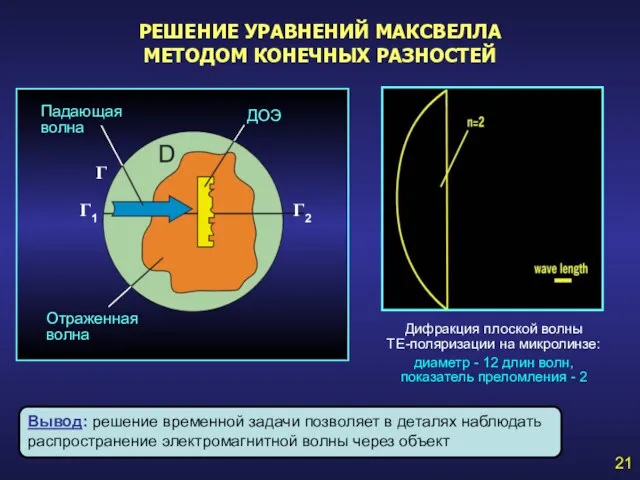
21
Γ1
Γ
Γ2
Падающая
волна
Отраженная
волна
ДОЭ
Дифракция плоской волны
ТЕ-поляризации на микролинзе:
диаметр - 12 длин волн,
показатель преломления - 2
РЕШЕНИЕ УРАВНЕНИЙ МАКСВЕЛЛА
МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ
Вывод: решение временной задачи позволяет в деталях наблюдать
распространение электромагнитной волны через объект

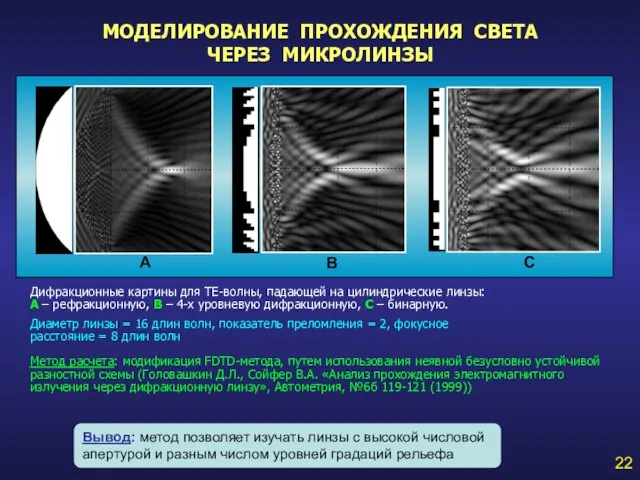
МОДЕЛИРОВАНИЕ ПРОХОЖДЕНИЯ СВЕТА
ЧЕРЕЗ МИКРОЛИНЗЫ
22
Дифракционные картины для ТЕ-волны, падающей на цилиндрические линзы: А – рефракционную, В – 4-х уровневую дифракционную, С – бинарную.
Диаметр линзы = 16 длин волн, показатель преломления = 2, фокусное
расстояние = 8 длин волн
Метод расчета: модификация FDTD-метода, путем использования неявной безусловно устойчивой
разностной схемы (Головашкин Д.Л., Сойфер В.А. «Анализ прохождения электромагнитного излучения через дифракционную линзу», Автометрия, №6б 119-121 (1999))
Вывод: метод позволяет изучать линзы с высокой числовой
апертурой и разным числом уровней градаций рельефа

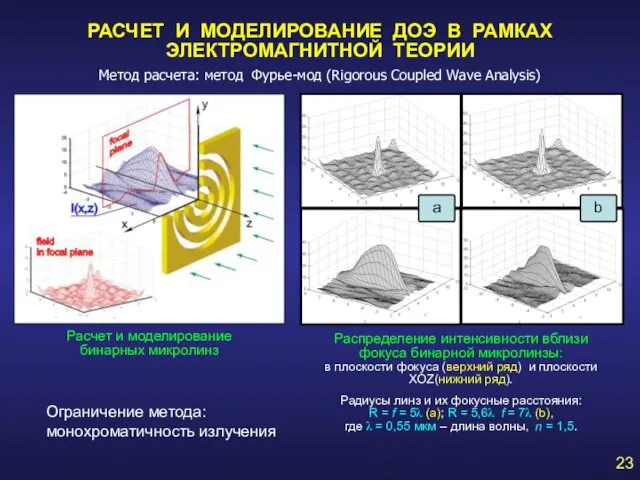
РАСЧЕТ И МОДЕЛИРОВАНИЕ ДОЭ В РАМКАХ ЭЛЕКТРОМАГНИТНОЙ ТЕОРИИ
Расчет и моделирование
бинарных микролинз
Распределение интенсивности вблизи фокуса бинарной микролинзы:
в плоскости фокуса (верхний ряд) и плоскости XOZ(нижний ряд).
Радиусы линз и их фокусные расстояния:
R = f = 5λ (a); R = 5,6λ f = 7λ (b),
где λ = 0,55 мкм – длина волны, n = 1,5.
23
Метод расчета: метод Фурье-мод (Rigorous Coupled Wave Analysis)
Ограничение метода:
монохроматичность излучения

РАЗРЕШЕНИЕ УСТРОЙСТВ ЗАПИСИ СИНТЕЗИРОВАННОГО ОПТИЧЕСКОГО МИКРОРЕЛЬЕФА
Электронный микроскоп LEO 1530 SEM
с литографической приставкой RAITH ELPHY (разрешение 50 нм)
* Заметим, что ДОЭ с линейными и круговыми зонами микрорельефа записываются в настоящее время с помощью делительных машин и других устройств записи с разрешением 50 нм.
24
ЧАСТЬ II. ДКО и нанофотоника

ДИФРАКЦИОННАЯ КОМПЬЮТЕРНАЯ ОПТИКА
И НАНОФОТОНИКА
Нанофотоника изучает поведение света в наноразмерной области
и обеспечивает проектирование оптических устройств в наномасштабе (Wikipedia)
Прогресс во многих областях нанофотоники существенно зависит
от прогресса в развитии дифракционной компьютерной оптики:
метаматериалы; фотонные кристаллы; плазмоника;
оптический захват и микроманипулирование; наномоделирование.
Международная конференция
по оптике и фотонике (Optics & Photonics),
Сан Диего, США, 2009
Международная конференция
по фотонике (Photonics Europe),
Брюссель, Бельгия, 2010
25

ПРИМЕНЕНИЕ ДОЭ В МИКРОМЕХАНИКЕ
26
ДОЭ могут быть использованы не только для информационных оптических систем, но и для механических применений.
В этом случае энергия лазерного пучка преобразуется в механическую энергию движения микрочастицы
или микродетали
Преобразование спинового углового момента лазерного пучка с круговой
поляризацией во вращающийся момент частицы с двойным лучепреломлением
(1 мкм CaCO2) (1), далее во вращающийся момент жидкости и потом
во вращающийся момент шестеренки (10 мкм, плавленный кварц) (2).
1
2
1873г.- расчет светового давления в рамках электродинамике (Дж. Максвелл)
1879г.- расчет светового давления в рамках термодинамики (А. Бартоли)
1898г.- опыты по измерению светового давления (П.Н. Лебедев)
1970г.- захват микрообъектов в лазерных пучках (А. Эшкин )
1996г.- захват микрообъектов в вихревых световых пучках (K. T. Gahagan)
1996г.- вращение микрообъекта в вихревых световых пучках, полученных
с помощью амплитудных голограмм (M. E Friese)
2001г.- использование ДОЭ для оптического захвата группы микрообъектов(Y. Ogura)
2004г.- использование многопорядковых ДОЭ для оптического захвата и
вращения микрообъектов (Р.В. Скиданов, В.А. Сойфер)
2008г.- оптическая сортировка микрочастиц по размерам (K. Dholakia)
2010г.- захват микрочастицы с помощью возбужденной микро антенны (K. Dholakia)

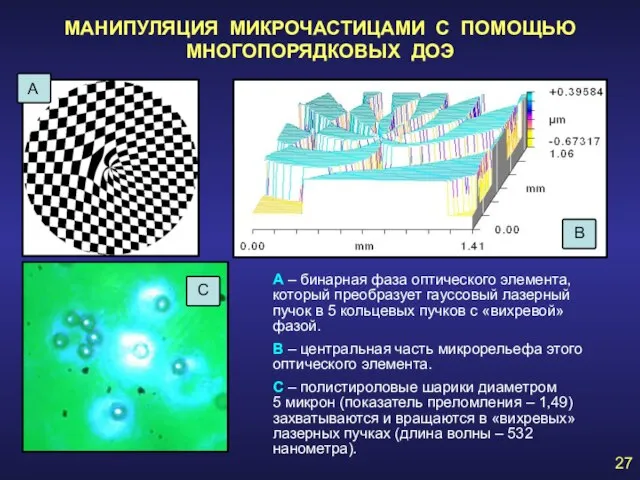
МАНИПУЛЯЦИЯ МИКРОЧАСТИЦАМИ С ПОМОЩЬЮ МНОГОПОРЯДКОВЫХ ДОЭ
А – бинарная фаза оптического элемента,
который преобразует гауссовый лазерный пучок в 5 кольцевых пучков с «вихревой» фазой.
В – центральная часть микрорельефа этого
оптического элемента.
С – полистироловые шарики диаметром
5 микрон (показатель преломления – 1,49)
захватываются и вращаются в «вихревых»
лазерных пучках (длина волны – 532 нанометра).
27
В
А

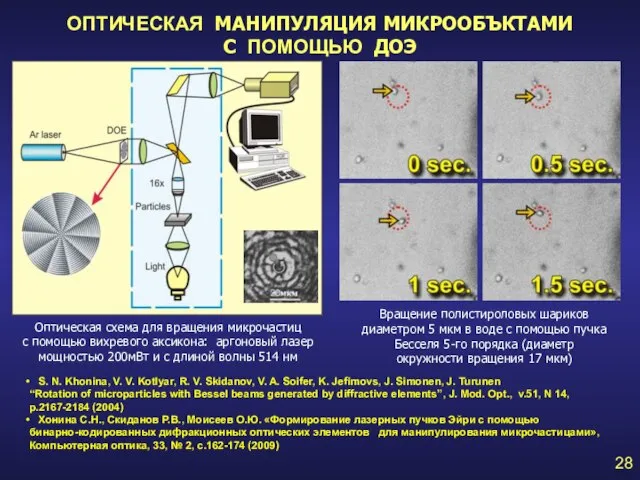
Вращение полистироловых шариков диаметром 5 мкм в воде с помощью пучка Бесселя 5-го порядка (диаметр
окружности вращения 17 мкм)
ОПТИЧЕСКАЯ МАНИПУЛЯЦИЯ МИКРООБЪКТАМИ
С ПОМОЩЬЮ ДОЭ
28
Оптическая схема для вращения микрочастиц
с помощью вихревого аксикона: аргоновый лазер мощностью 200мВт и с длиной волны 514 нм
S. N. Khonina, V. V. Kotlyar, R. V. Skidanov, V. A. Soifer, K. Jefimovs, J. Simonen, J. Turunen
“Rotation of microparticles with Bessel beams generated by diffractive elements”, J. Mod. Opt., v.51, N 14,
p.2167-2184 (2004)
Хонина С.Н., Скиданов Р.В., Моисеев О.Ю. «Формирование лазерных пучков Эйри с помощью
бинарно-кодированных дифракционных оптических элементов для манипулирования микрочастицами»,
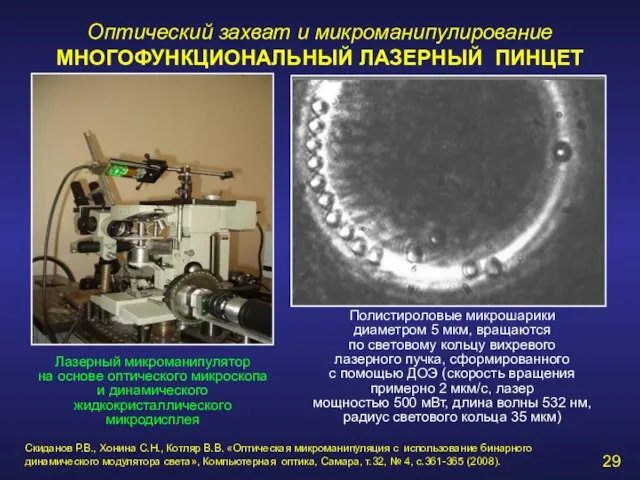
Компьютерная оптика, 33, № 2, с.162-174 (2009)

Оптический захват и микроманипулирование
МНОГОФУНКЦИОНАЛЬНЫЙ ЛАЗЕРНЫЙ ПИНЦЕТ
Лазерный микроманипулятор
на основе оптического микроскопа
и динамического
жидкокристаллического
микродисплея
Полистироловые микрошарики
диаметром 5 мкм, вращаются
по световому кольцу вихревого
лазерного пучка, сформированного
с помощью ДОЭ (скорость вращения
примерно 2 мкм/с, лазер
мощностью 500 мВт, длина волны 532 нм,
радиус светового кольца 35 мкм)
Скиданов Р.В., Хонина С.Н., Котляр В.В. «Оптическая микроманипуляция с использование бинарного динамического модулятора света», Компьютерная оптика, Самара, т.32, № 4, с.361-365 (2008).
29

Фотонно-кристаллические структуры
МЕТАЛЛИЧЕСКИЕ НАНОСТЕРЖНИ
дифракция ТЕ волны на металлическом (A), диэлектрическом микро-цилиндре (B)
и на микро-цилиндре с металлическими нано-стержнями диаметром 5 нм (C)
Диэлектрический цилиндр (ε = 2,25 )
с диаметром 1мкм, заполнен стержнями из серебра (ε = – 9,49 + 1,483i ) диаметром 5 нм, освещается светом с длиной волны – 0,5 мкм.
Выбором величины периода решетки стержней, можно добиться единичного значения реальной части диэлектрической проницаемости и обеспечить минимальную дифракцию света на цилиндре
Компьютерная оптика, т.32, № 1, с. 23-28 (2008).
30

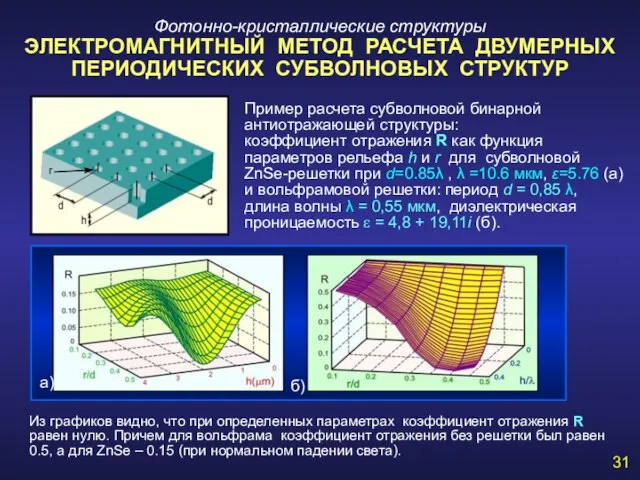
Фотонно-кристаллические структуры
ЭЛЕКТРОМАГНИТНЫЙ МЕТОД РАСЧЕТА ДВУМЕРНЫХ ПЕРИОДИЧЕСКИХ СУБВОЛНОВЫХ СТРУКТУР
Пример расчета субволновой бинарной
антиотражающей структуры:
коэффициент отражения R как функция
параметров рельефа h и r для субволновой
ZnSe-решетки при d=0.85λ , λ =10.6 мкм, ε=5.76 (а)
и вольфрамовой решетки: период d = 0,85 λ,
длина волны λ = 0,55 мкм, диэлектрическая
проницаемость ε = 4,8 + 19,11i (б).
Из графиков видно, что при определенных параметрах коэффициент отражения R
равен нулю. Причем для вольфрама коэффициент отражения без решетки был равен
0.5, а для ZnSe – 0.15 (при нормальном падении света).
а)
б)
31

Фотонно-кристаллические структуры
ФОТОННО-КРИСТАЛЛИЧЕСКАЯ ЛИНЗА В ВОЛНОВОДЕ
Моделирование (А) и эксперимент (Б) по прохождению света через два волновода разной
толщины, связанных ФК-линзой
Вид сверху (в СЭМ) 2D ФК-линза
и волноводы в пленке кремния
(n=2,83) для длины волны 1,55 мкм.
Диаметр отверстий линзы вариьруется от 160 нм до 200 нм.
А
Appl. Opt., v.48, no.19, p.3722-3730 (2009)
Б
32

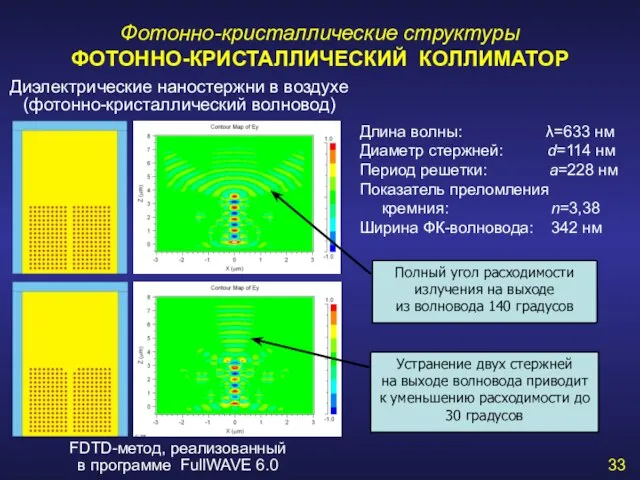
Фотонно-кристаллические структуры
ФОТОННО-КРИСТАЛЛИЧЕСКИЙ КОЛЛИМАТОР
Длина волны: λ=633 нм
Диаметр стержней: d=114 нм
Период решетки: a=228 нм
Показатель преломления
кремния: n=3,38
Ширина ФК-волновода: 342 нм
FDTD-метод, реализованный
в программе FullWAVE 6.0
Диэлектрические наностержни в воздухе
(фотонно-кристаллический волновод)
Полный угол расходимости
излучения на выходе
из волновода 140 градусов
Устранение двух стержней
на выходе волновода приводит к уменьшению расходимости до 30 градусов
33

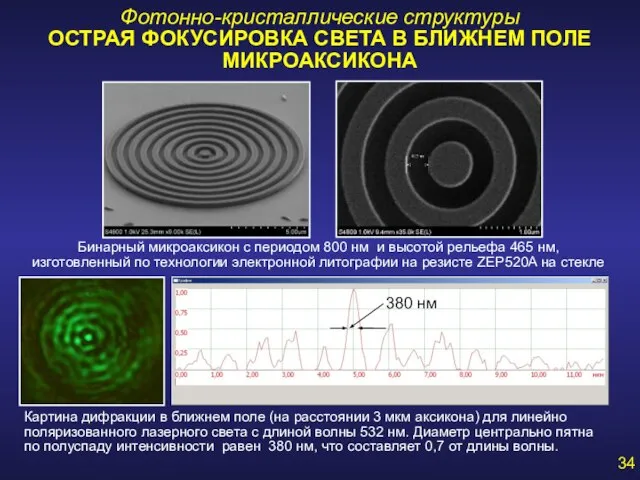
Фотонно-кристаллические структуры
ОСТРАЯ ФОКУСИРОВКА СВЕТА В БЛИЖНЕМ ПОЛЕ
МИКРОАКСИКОНА
Бинарный микроаксикон с периодом 800 нм и высотой рельефа 465 нм,
изготовленный по технологии электронной литографии на резисте ZEP520A на стекле
Картина дифракции в ближнем поле (на расстоянии 3 мкм аксикона) для линейно поляризованного лазерного света с длиной волны 532 нм. Диаметр центрально пятна по полуспаду интенсивности равен 380 нм, что составляет 0,7 от длины волны.
380 нм
34

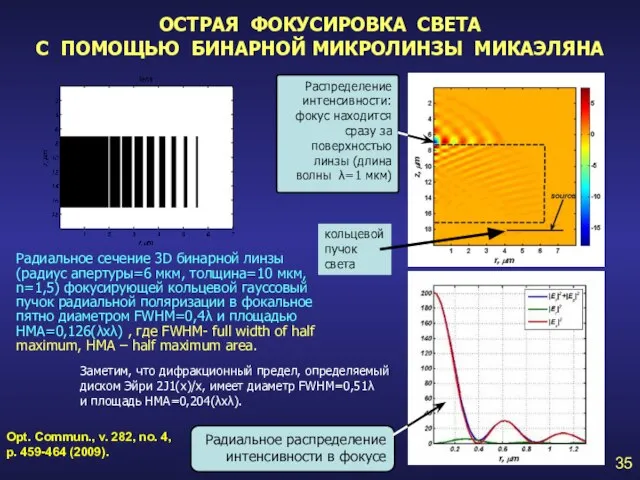
ОСТРАЯ ФОКУСИРОВКА СВЕТА
С ПОМОЩЬЮ БИНАРНОЙ МИКРОЛИНЗЫ МИКАЭЛЯНА
35
Радиальное сечение 3D бинарной линзы (радиус апертуры=6 мкм, толщина=10 мкм, n=1,5) фокусирующей кольцевой гауссовый пучок радиальной поляризации в фокальное пятно диаметром FWHM=0,4λ и площадью HMA=0,126(λxλ) , где FWHM- full width of half maximum, HMA – half maximum area.
Распределение интенсивности: фокус находится сразу за поверхностью
линзы (длина
волны λ=1 мкм)
Радиальное распределение
интенсивности в фокусе
Заметим, что дифракционный предел, определяемый
диском Эйри 2J1(x)/x, имеет диаметр FWHM=0,51λ
и площадь HMA=0,204(λxλ).
кольцевой
пучок
света
Opt. Commun., v. 282, no. 4,
p. 459-464 (2009).

Управление магнитооптическими гетеронаноструктурами
РЕЗОНАНСНЫЕ МАГНИТООПТИЧЕСКИЕ ЭФФЕКТЫ
В МЕТАЛЛОДИЭЛЕКТРИЧЕСКИХ ГЕТЕРОСТРУКТУРАХ
(совм. результат с ИОФ РАН и МГУ)
Cтруктура состоит из дифракционной решётки (Au) и намагниченного в плоскости диэлектрического слоя (редкоземельный феррит-гранат). Характерные размеры r, hgr ~50нм.
Эффект состоит в резонансной зависимости пропускания (отражения) структуры от величины намагниченности.
Практические применения: транспаранты и датчики, основанные на модуляции интенсивности (поляризации) света при изменении внешнего магнитного поля.
1. Optics Letters, 2009, 34 (4), pp. 398-400.
2. Физика твердого тела, 2009, 51(8), с. 1562-1567.
Спектры отражения R(λ) и пропускания T(λ) при намагниченном слое (сплошная линия) и при отсутствии намагниченности (пунктир)
36

Управление магнитооптическими гетеронаноструктурами
ЭКСТРАОРДИНАРНОЕ ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ
В МЕТАЛЛОДИЭЛЕКТРИЧЕСКИХ ГЕТЕРОСТРУКТУРАХ
(совм. результат с ИОФ РАН и МГУ)
Структура состоит из 2-х дифракционных решёток (Au) и намагниченного диэлектрического слоя (редкоземельный феррит-гранат).
Характерные размеры r, hgr ~100 нм.
Спектры пропускания и угла Фарадея.
При λ= 832 нм имеется острый пик пропускания (>45%), совмещенный с резонансом угла Фарадея (-130). Угол Фарадея в 17 раз больше, чем для однородного магнитного слоя такой же толщины (830 нм).
Практические применения: датчики, модуляция поляризации света.
1. Physical Review Letters, 2007, 98, pp. 077401(4) .
2. Компьютерная оптика, 2007, 31(1), с. 4-8.
Эффект состоит в резонансном вращении плоскости поляризации в структурах, состоящих из перфорированных металлических и однородных слоев намагниченных в полярной геометрии.
37

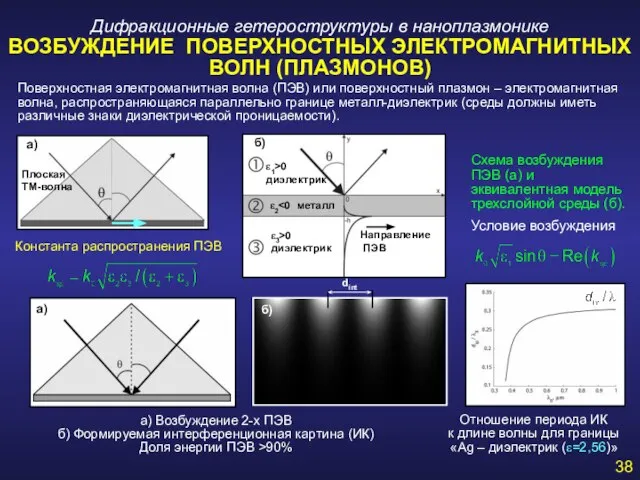
Дифракционные гетероструктуры в наноплазмонике
ВОЗБУЖДЕНИЕ ПОВЕРХНОСТНЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН (ПЛАЗМОНОВ)
а) Возбуждение 2-х ПЭВ
б) Формируемая интерференционная картина (ИК)
Доля энергии ПЭВ >90%
Поверхностная электромагнитная волна (ПЭВ) или поверхностный плазмон – электромагнитная волна, распространяющаяся параллельно границе металл-диэлектрик (среды должны иметь различные знаки диэлектрической проницаемости).
Схема возбуждения ПЭВ (а) и эквивалентная модель трехслойной среды (б).
Условие возбуждения
Отношение периода ИК
к длине волны для границы «Ag – диэлектрик (ε=2,56)»
б)
Константа распространения ПЭВ
dint
а)
38

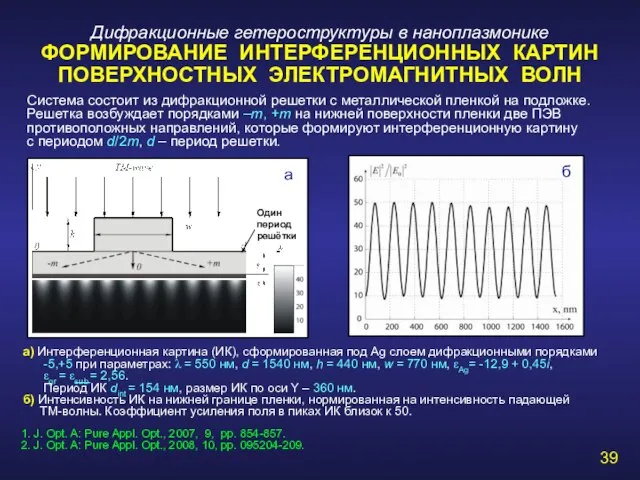
Дифракционные гетероструктуры в наноплазмонике
ФОРМИРОВАНИЕ ИНТЕРФЕРЕНЦИОННЫХ КАРТИН ПОВЕРХНОСТНЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Система состоит из дифракционной решетки с металлической пленкой на подложке.
Решетка возбуждает порядками –m, +m на нижней поверхности пленки две ПЭВ противоположных направлений, которые формируют интерференционную картину
с периодом d/2m, d – период решетки.
a) Интерференционная картина (ИК), сформированная под Ag слоем дифракционными порядками
-5,+5 при параметрах: λ = 550 нм, d = 1540 нм, h = 440 нм, w = 770 нм, εAg= -12,9 + 0,45i, εgr = εsub = 2,56. Период ИК dint = 154 нм, размер ИК по оси Y – 360 нм.
б) Интенсивность ИК на нижней границе пленки, нормированная на интенсивность падающей ТМ-волны. Коэффициент усиления поля в пиках ИК близок к 50.
1. J. Opt. A: Pure Appl. Opt., 2007, 9, pp. 854-857.
2. J. Opt. A: Pure Appl. Opt., 2008, 10, pp. 095204-209.
Один
период
решётки
39

a) Трехмерная диэлектрическая бинарная дифракционная решетка (d = 923 нм, ε = 2.56, площадь квадратного отверстия – 0.26dx0.26d) с Ag- пленкой (h = 70 нм).
Структура предполагается расположенной на резисте (ε = 2.56).
б) Интерференционная картина, формируемая на нижней границе Ag-пленки и резиста
в пределах периода при длине волны 550 нм.
a
б
Дифракционные гетероструктуры в наноплазмонике
ФОРМИРОВАНИЕ ДВУМЕРНЫХ ИНТЕРФРЕНЦИОННЫХ КАРТИН
ПОВЕРХНОСТНЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Интерференционная картина (ИК) формируется ПЭВ, возбужденными порядками (-3,0), (+3,0),
(0,-3), (0,+3). Период ИК dint=154 нм в 6 раз меньше периода решетки. Интенсивность в максимумах ИК на порядок больше интенсивности падающей на решетку волны.
40

Дифракционные гетероструктуры в наноплазмонике
УПРАВЛЕНИЕ СТРУКТУРОЙ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ
ЗА СЧЕТ ИЗМЕНЕНИЯ ПОЛЯРИЗАЦИИ ПАДАЮЩЕЙ ВОЛНЫ
Интерференционные картины (ИК), формируемые на нижней границе Ag-пленки
в пределах периода, при различных поляризациях падающей волны
(ИК формируются 4 ПЭВ).
Линейная TM-поляризация
Линейная поляризация
(50% TE & 50% TM)
Круговая поляризация
Линейная поляризация
(10% TE & 90% TM)
Эллиптическая поляризация
41

Дифракционные гетероструктуры в наноплазмонике
УПРАВЛЕНИЕ СТРУКТУРОЙ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ
ЗА СЧЕТ ИЗМЕНЕНИЯ ДЛИНЫ ВОЛНЫ
ПАДАЮЩЕГО ИЗЛУЧЕНИЯ
Интерференционные картины (ИК), формируемые на нижней границе Ag-пленки
в пределах периода, при различных длинах волн.
Поляризация падающей волны – круговая.
λ = 550 нм λ = 774 нм λ = 532 нм
(4 ПЭВ, период ИК-154нм) (4 ПЭВ, период ИК-308 нм) (8 ПЭВ)
Компьютерная оптика, 2009, 33(1), с. 9-16.
Optics Communications, 2010, 283, pp. 2020-2025.
42

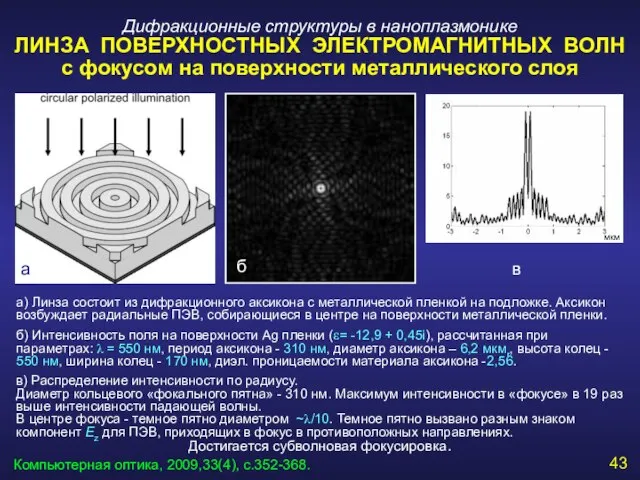
Дифракционные структуры в наноплазмонике
ЛИНЗА ПОВЕРХНОСТНЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
с фокусом на поверхности металлического слоя
а) Линза состоит из дифракционного аксикона с металлической пленкой на подложке. Аксикон возбуждает радиальные ПЭВ, собирающиеся в центре на поверхности металлической пленки.
б) Интенсивность поля на поверхности Ag пленки (ε= -12,9 + 0,45i), рассчитанная при параметрах: λ = 550 нм, период аксикона - 310 нм, диаметр аксикона – 6,2 мкмr, высота колец - 550 нм, ширина колец - 170 нм, диэл. проницаемости материала аксикона -2,56.
в) Распределение интенсивности по радиусу.
Диаметр кольцевого «фокального пятна» - 310 нм. Максимум интенсивности в «фокусе» в 19 раз выше интенсивности падающей волны.
В центре фокуса - темное пятно диаметром ~λ/10. Темное пятно вызвано разным знаком компонент Ez для ПЭВ, приходящих в фокус в противоположных направлениях.
Достигается субволновая фокусировка.
a
б
в
мкм
43
Компьютерная оптика, 2009,33(4), с.352-368.

ФОКУСИРОВКА ПОВЕРХНОСТНЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ПОМОЩЬЮ ДОЭ
Модель дифракции ПЭВ: Расчет ЭМ поля непосредственно за ДОЭ основан на строгом решении базовой задачи дифракции ПЭВ на диэлектрической ступеньке. Длина l и высота h ступеньки совпадают с длиной и высотой микрорельефа ДОЭ в рассматриваемой точке. Для описания дальнейшего распространения и дифракции ПЭВ используется интеграл Кирхгофа для ПЭВ.
Метод расчета ДОЭ: Расчет основан на модуляции фазы ПЭВ за счет изменения высоты и длины дифракционного микрорельефа. Функция фазовой модуляции рассчитывается с использованием методов скалярной теории дифракции.
44
Компьютерная оптика, 2009,33(2), с.122-128.
Journal of Optics, 2010, 12, pp. 015001-8
ДОЭ выполнен в виде диэлектрической дифракционной структуры расположенной на границе распространения ПЭВ.
ДОЭ выполнен в виде симметричной дифракционной структуры, расположенной на обеих сторонах плазмонного волновода (тонкой металлической пленки).

БАЗОВАЯ ЗАДАЧА ДИФРАКЦИИ И ИНТЕГРАЛ КИРХГОФА
Геометрия прохождения ПЭВ через диэлектрическую ступеньку, расположенную на границе раздела (а) и по обеим сторонам металлической пленки (б)
(εm,εd,εb – диэлектрические проницаемости металла, диэлектрика и материала ступеньки).
Решение базовой задачи проводится по методу Фурье-мод для апериодических структур
(E. Silberstein, P. Lalanne, J. Hugonin, Q. Cao, JOSA A, 2001).
В результате многократного решения базовой задачи рассчитывается поле H(y) на выходе ДОЭ при x=0. Необходимая дискретизация (число решений базовой задачи) определяется размером минимальной зоны функции фазовой модуляции). Последующее распространение поля определяется через расчет интеграла Кирхгофа для ПЭВ:
а)
б)
где kSPP – константа распространения ПЭВ границы раздела или мет. пленки.
45

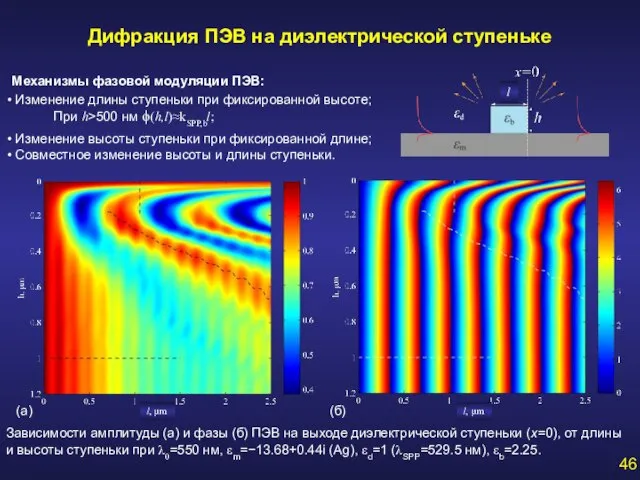
Дифракция ПЭВ на диэлектрической ступеньке
Зависимости амплитуды (а) и фазы (б) ПЭВ на выходе диэлектрической ступеньки (x=0), от длины и высоты ступеньки при λ0=550 нм, εm=−13.68+0.44i (Ag), εd=1 (λSPP=529.5 нм), εb=2.25.
Механизмы фазовой модуляции ПЭВ:
Изменение длины ступеньки при фиксированной высоте;
При h>500 нм ϕ(h,l)≈kSPP,bl;
Изменение высоты ступеньки при фиксированной длине;
Совместное изменение высоты и длины ступеньки.
46
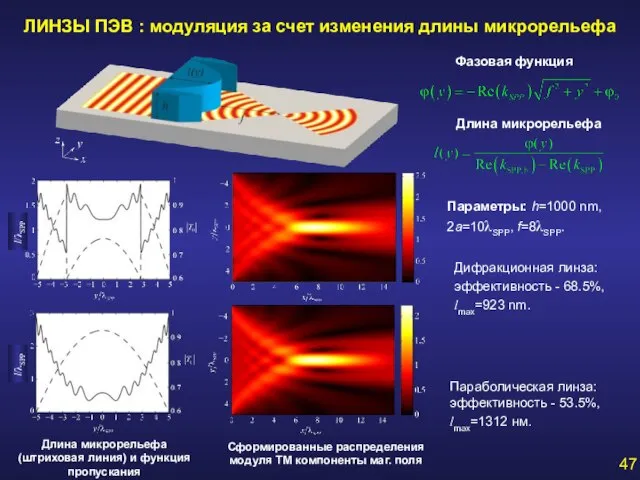
(а)
(б)

ЛИНЗЫ ПЭВ : модуляция за счет изменения длины микрорельефа
Длина микрорельефа (штриховая линия) и функция пропускания
Параболическая линза: эффективность - 53.5%,
lmax=1312 нм.
Фазовая функция
Дифракционная линза:
эффективность - 68.5%,
lmax=923 nm.
Сформированные распределения модуля ТМ компоненты маг. поля
Длина микрорельефа
Параметры: h=1000 nm,
2a=10λSPP, f=8λSPP.
47

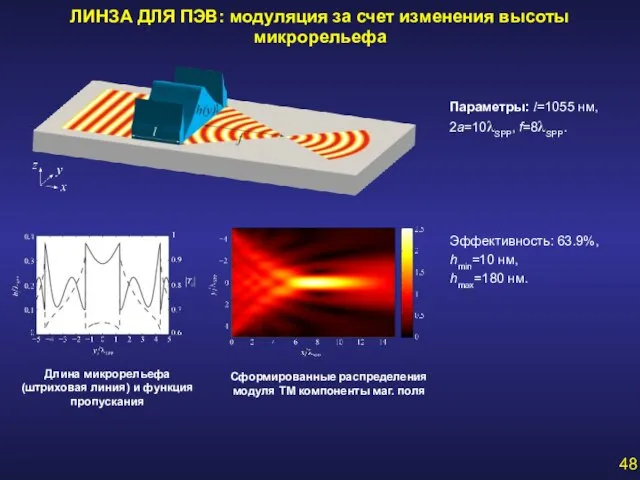
ЛИНЗА ДЛЯ ПЭВ: модуляция за счет изменения высоты микрорельефа
Эффективность: 63.9%,
hmin=10 нм,
hmax=180 нм.
Параметры: l=1055 нм,
2a=10λSPP, f=8λSPP.
Длина микрорельефа (штриховая линия) и функция пропускания
Сформированные распределения модуля ТМ компоненты маг. поля
48

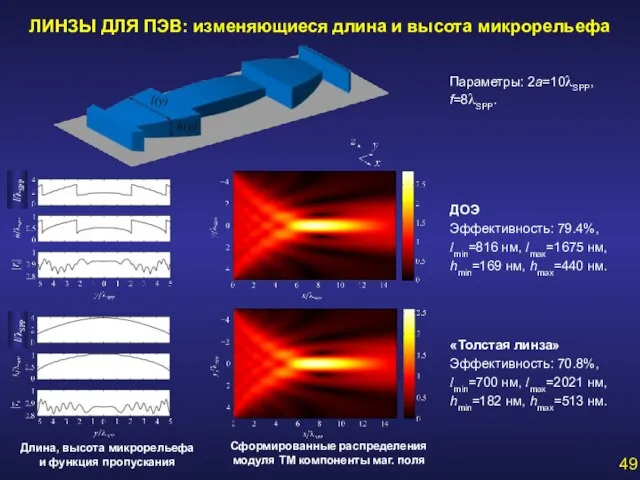
ЛИНЗЫ ДЛЯ ПЭВ: изменяющиеся длина и высота микрорельефа
ДОЭ
Эффективность: 79.4%,
lmin=816 нм, lmax=1675 нм,
hmin=169 нм, hmax=440 нм.
«Толстая линза»
Эффективность: 70.8%,
lmin=700 нм, lmax=2021 нм,
hmin=182 нм, hmax=513 нм.
Параметры: 2a=10λSPP, f=8λSPP.
Длина, высота микрорельефа и функция пропускания
Сформированные распределения модуля ТМ компоненты маг. поля
49

Многофокусные линзы ПЭВ: модуляция за счет изменения длины
Функция фазовой модуляции соответствует суперпозиции фазовой функции линзы и N-порядковой дифракционной решетки:
Распределения модуля ТМ-компоненты магнитного поля для двухфокусной и трехфокусной линз при параметрах: h=1000 nm, 2a=20λSPP, f=10λSPP, d=2.5λSPP.
Длина микрорельефа:
Фазовые функции дифракционных решеток с 2-мя и 3-мя основными порядками:
50

Линзы для ПЭВ, распространяющихся в металлической пленке: модуляция за счет изменения длины микрорельефа
Длина микрорельефа
Распределение модуля ТМ компоненты маг. поля для линзы
(h=1000 nm, 2a=10λLRSP, f=8λLRSP)
Сформированные распределения модуля ТМ компоненты маг. поля для двухфокусных линз (h=1000 nm 2a=10λLRSP)
51