Содержание
- 2. Динамические модели управления запасами. В действительности запасы не являются однородными по времени с точки зрения оптимальности.
- 3. 100 100 100 100 производство М1 0 1 2 3 4 5 6 7 8 9
- 4. 150 150 150 150 производство М2 0 1 2 3 4 5 6 7 8 9
- 5. 200 300 200 300 200 300 200 300 200 производство S 0 1 2 3 4
- 6. Модель при отсутствии затрат на оформление заказа. При неодинаковом технологическом процессе производства необходимо производить продукцию при
- 7. Пример: Компания производит вытяжки, которые используются в каминах с декабря по март. В начале сезона спрос
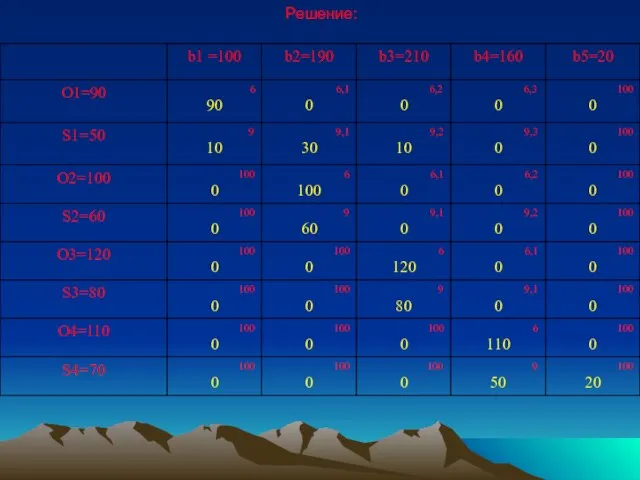
- 8. Решение:
- 10. Скачать презентацию
Слайд 2Динамические модели управления запасами.
В действительности запасы не являются однородными по времени с
Динамические модели управления запасами.
В действительности запасы не являются однородными по времени с
В действительности запасы не являются однородными по времени с

точки зрения оптимальности. Это связано с сезонными колебаниями или технологическими условиями.
Пример:
На протяжении года квартальный спрос на модели М1 и М2 некоторой продукции равен 100 и 150 единиц соответственно. Поставки реализуются в конце каждого квартала. Сроки выполнения заказа на модели М1 и М2 равны 2 и 1 месяц соответственно. Для изготовления единицы М1 и М2 используются 2 единицы комплектующих S, срок изготовления которых – 1 месяц. Составить модель производства S.
Пример:
На протяжении года квартальный спрос на модели М1 и М2 некоторой продукции равен 100 и 150 единиц соответственно. Поставки реализуются в конце каждого квартала. Сроки выполнения заказа на модели М1 и М2 равны 2 и 1 месяц соответственно. Для изготовления единицы М1 и М2 используются 2 единицы комплектующих S, срок изготовления которых – 1 месяц. Составить модель производства S.
Слайд 6Модель при отсутствии затрат на оформление заказа.
При неодинаковом технологическом процессе производства необходимо
Модель при отсутствии затрат на оформление заказа.
При неодинаковом технологическом процессе производства необходимо
При неодинаковом технологическом процессе производства необходимо

производить продукцию при следующих условиях:
отсутствие затрат на оформление
отсутствие дефицита
стоимость производства единицы продукта в любой период времени является постоянной величиной либо имеет возрастающие предельные затраты. Возможные режимы работы: обычный, интенсивный, сверхурочный и т. п.
стоимость хранения единицы продукта в любой период времени постоянна.
Задачу можно решить для «n» - этапного процесса с «k» - возможными уровнями производства как транспортную задачу с n*k пунктами производства и пунктами потребления, равными объёму производства каждого месяца.
В решении задачи достаточно построить решение, которое будет оптимальным по следующему алгоритму:
Себестоимость перевозок определяется как суммарные издержки на производство и содержание продукта для каждого этапа и режима работы. Оптимальное решение получается за один проход с заполнения 1 – го столбца, затем второго и т. д. по методу наименьшей стоимости.
отсутствие затрат на оформление
отсутствие дефицита
стоимость производства единицы продукта в любой период времени является постоянной величиной либо имеет возрастающие предельные затраты. Возможные режимы работы: обычный, интенсивный, сверхурочный и т. п.
стоимость хранения единицы продукта в любой период времени постоянна.
Задачу можно решить для «n» - этапного процесса с «k» - возможными уровнями производства как транспортную задачу с n*k пунктами производства и пунктами потребления, равными объёму производства каждого месяца.
В решении задачи достаточно построить решение, которое будет оптимальным по следующему алгоритму:
Себестоимость перевозок определяется как суммарные издержки на производство и содержание продукта для каждого этапа и режима работы. Оптимальное решение получается за один проход с заполнения 1 – го столбца, затем второго и т. д. по методу наименьшей стоимости.
Слайд 7Пример:
Компания производит вытяжки, которые используются в каминах с декабря по март. В
Пример:
Компания производит вытяжки, которые используются в каминах с декабря по март. В
Компания производит вытяжки, которые используются в каминах с декабря по март. В

начале сезона спрос низкий, в середине достигает пика и уменьшается к концу. Учитывая популярность продукции, компания мажет использовать сверхурочные работы для удовлетворения спроса.
Месяц Объём производства Объём сверхурочного производства Спрос
Декабрь 90 50 100
Январь 100 60 190
Февраль 120 80 210
Март 110 70 160
Стоимость производства продукции равна 6 у. е. при обычном режиме работы и 9 у. е. – при сверхурочном. Стоимость хранения – 0,1 у. е. в месяц.
Пусть Oi - количество продукции, произведённой обычным способом, Si – сверхурочным.
n=4 k=2
Месяц Объём производства Объём сверхурочного производства Спрос
Декабрь 90 50 100
Январь 100 60 190
Февраль 120 80 210
Март 110 70 160
Стоимость производства продукции равна 6 у. е. при обычном режиме работы и 9 у. е. – при сверхурочном. Стоимость хранения – 0,1 у. е. в месяц.
Пусть Oi - количество продукции, произведённой обычным способом, Si – сверхурочным.
n=4 k=2
Слайд 8Решение:
Решение:



 Классное ученическое собрание- одна из форм привлечения учащихся к самоуправлению
Классное ученическое собрание- одна из форм привлечения учащихся к самоуправлению Организационно-распорядительная документация общеобразовательных учреждений на конец учебного года
Организационно-распорядительная документация общеобразовательных учреждений на конец учебного года Все ли йогурты полезны
Все ли йогурты полезны ОБРАЗОВАТЕЛЬНАЯ СРЕДА ШКОЛЫ как синтез образовательных ресурсов
ОБРАЗОВАТЕЛЬНАЯ СРЕДА ШКОЛЫ как синтез образовательных ресурсов Принятие решений на префлопе в рейженных банках. Покер
Принятие решений на префлопе в рейженных банках. Покер Живопись
Живопись Экономическое чудо.
Экономическое чудо. Организация питания В МАДОУ Детский сад № 377 г. Перми
Организация питания В МАДОУ Детский сад № 377 г. Перми Децентрализация лесоустроительных работ как необходимая реальность развития лесных отношений
Децентрализация лесоустроительных работ как необходимая реальность развития лесных отношений Публичное выступление и презентация
Публичное выступление и презентация 150 ЛЕТ ГУМАНИТАРНОЙ ДЕЯТЕЛЬНОСТИ
150 ЛЕТ ГУМАНИТАРНОЙ ДЕЯТЕЛЬНОСТИ  Конструирование. Снятие мерок с фигуры человека. 7 класс
Конструирование. Снятие мерок с фигуры человека. 7 класс Классификация и морфология микроорганизмов
Классификация и морфология микроорганизмов Одноклеточные паразиты
Одноклеточные паразиты Как стать избирателем на предварительном голосовании Единой России
Как стать избирателем на предварительном голосовании Единой России Эффективность работы персонала в организации
Эффективность работы персонала в организации Ядерный (атомный) реактор
Ядерный (атомный) реактор Проект, его структура
Проект, его структура Правила дорожного движения
Правила дорожного движения Философия и наука
Философия и наука Основы цветоведения
Основы цветоведения Синдром диабетической стопы
Синдром диабетической стопы Место проведения экспедиции
Место проведения экспедиции Борьба с допингом на современном этапе Выходец Игорь Трифановичзаместитель директора Центра спортивных инновационных техноло
Борьба с допингом на современном этапе Выходец Игорь Трифановичзаместитель директора Центра спортивных инновационных техноло Анализ продажи алкоголя в Санкт-Петербурге (микрорайон метро Озерки)
Анализ продажи алкоголя в Санкт-Петербурге (микрорайон метро Озерки) «Свод-WEB» формирование регламентированной и произвольной отчетности в WEB-технологии»
«Свод-WEB» формирование регламентированной и произвольной отчетности в WEB-технологии» План коррекционной работы в детском дошкольном и игровом учреждении Федор и Варвара
План коррекционной работы в детском дошкольном и игровом учреждении Федор и Варвара Гимнастика. Виды гимнастики
Гимнастика. Виды гимнастики