Содержание
- 2. 1. ПРЕДМЕТ КУРСА Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил.
- 3. 2. МАТЕРИАЛЬНАЯ ТОЧКА Вообще говоря, одновременно с изменением положения тело может вращаться и деформироваться. Рассматривая движение
- 4. 3. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ Основные законы (аксиомы) динамики устанавливают связь между основными понятиями механики: массой, силой,
- 5. 4. ПЕРВЫЙ ЗАКОН ДИНАМИКИ Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения,
- 6. 5. ВТОРОЙ ЗАКОН ДИНАМИКИ В инерциальной системе изменение количества движения пропорционально приложенной силе и происходит по
- 7. 6. СЛЕДСТВИЯ 1) Из 2-го закона видно, чем больше масса точки, тем меньше её ускорение при
- 8. 7. ТРЕТИЙ ЗАКОН ДИНАМИКИ Действию всегда есть равное и противоположное противодействие Силы взаимодействия 2-х материальных точек
- 9. 8. ОСНОВНЫЕ ВИДЫ СИЛ Сила тяжести. м./c2 Сила трения скольжения коэффициент трения нормальная реакция. ускорение свободного
- 10. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ. дифференциальные уравнения движения точки в прямоугольных декартовых координатах дифференциальные уравнения движения
- 11. 10. ПЕРВАЯ ЗАДАЧА ДИНАМИКИ Первая задача динамики: зная закон движения точки, определить действующую на нее силу
- 12. 11. ПЕРВАЯ ЗАДАЧА ДИНАМИКИ Автомобиль движется с постоянной скоростью по мосту радиуса . Найти силу реакции
- 13. 12. ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ Вторая, или основная, задача динамики: зная действую-щие на точку силы, определить закон
- 14. 13. ПРИМЕР : ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ Н.У. при t=0
- 16. Скачать презентацию












 Смысловой конспект презентации
Смысловой конспект презентации Стратегии поведения родителей при поддержке детей в процессе подготовки ГИА
Стратегии поведения родителей при поддержке детей в процессе подготовки ГИА Аганбегян Абел Гезевич
Аганбегян Абел Гезевич Множества. Элемент множества. Подмножества.
Множества. Элемент множества. Подмножества. УРОК 2
УРОК 2 Пошив наволочек
Пошив наволочек Презентация по теме:«ПИЩЕВАРИТЕЛЬНАЯ СИСТЕМА»
Презентация по теме:«ПИЩЕВАРИТЕЛЬНАЯ СИСТЕМА» Хеликс: Автомойка и Шиномонтаж 8
Хеликс: Автомойка и Шиномонтаж 8 Актуальные правовые аспекты синдицированного кредитования
Актуальные правовые аспекты синдицированного кредитования Усовершенствование навыков на спринтерский бег
Усовершенствование навыков на спринтерский бег Длина окружности и площадь круга 5 класс
Длина окружности и площадь круга 5 класс Знакомство с праздником Масленица
Знакомство с праздником Масленица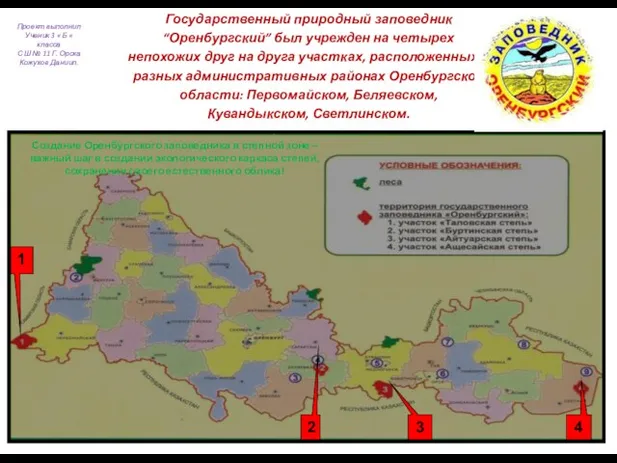 Оренбургский заповедник
Оренбургский заповедник Ценности корпоративной культуры РЭУ
Ценности корпоративной культуры РЭУ Обгрунтування системи охолодження турбо- та гідрогенераторів
Обгрунтування системи охолодження турбо- та гідрогенераторів Взаимосвязь государственной гражданской и муниципальной службы
Взаимосвязь государственной гражданской и муниципальной службы Дегустационные листы
Дегустационные листы Тема любви в повести А.И. Куприна "Гранатовый браслет"
Тема любви в повести А.И. Куприна "Гранатовый браслет" Заработок на облачном майнинге
Заработок на облачном майнинге Решение «Парковка» Обеспечивает: полностью автоматическое управление электромеханическим шлагбаумом, учет и контроль проезда ав
Решение «Парковка» Обеспечивает: полностью автоматическое управление электромеханическим шлагбаумом, учет и контроль проезда ав Новые стандарты – первые шаги
Новые стандарты – первые шаги Фасадное стекло
Фасадное стекло Слово как произведение искусства
Слово как произведение искусства Опера «Кармен» Ж.Бизе
Опера «Кармен» Ж.Бизе Фотоотчет УФМС, Архангельск
Фотоотчет УФМС, Архангельск История космических побед
История космических побед ПРАВА, ОБЯЗАННОСТИ и ОТВЕТСТВЕННОСТЬ ЧЕЛОВЕКА и ГРАЖДАНИНА
ПРАВА, ОБЯЗАННОСТИ и ОТВЕТСТВЕННОСТЬ ЧЕЛОВЕКА и ГРАЖДАНИНА История зарождения баскетбола. Современный баскетбол
История зарождения баскетбола. Современный баскетбол