ДОКАЗАТЕЛЬНОЕ ПРОЕКТИРОВАНИЕ РЕАКТИВНЫХ АЛГОРИТМОВ

РЕАКТИВНЫЕ СИСТЕМЫ
Под реактивными системами понимаются системы, постоянно взаимодействующие со своим окружением.
Примеры таких систем
системы управления технологическими процессами,
телекоммуникационные сети,
системы управления летательными аппаратами и др.
Функционирование таких систем состоит в выработке реакции на сигналы, поступающие из окружающей среды.

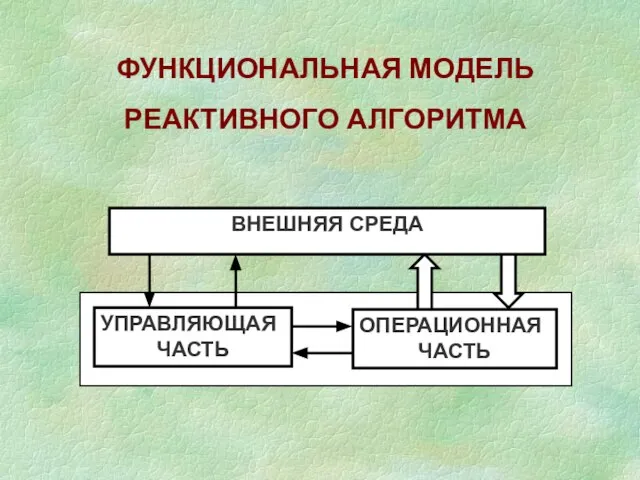
ФУНКЦИОНАЛЬНАЯ МОДЕЛЬ
РЕАКТИВНОГО АЛГОРИТМА

ПОДХОД К ПРОЕКТИРОВАНИЮ
При проектировании систем управления потенциально опасными объектами необходимо гарантировать точное соответствие алгоритма управления всем требованиям к функционированию системы.
В основе подхода лежит спецификация функциональных требований к системе в языке логики предикатов и формальный переход от спецификации к процедурному представлению алгоритма функционирования проектируемой системы.

ОСНОВНЫЕ ПОДХОДЫ К КОРРЕКТНОМУ ПРОЕКТИРОВАНИЮ РЕАКТИВНЫХ АЛГОРИТМОВ
ФОРМАЛЬНАЯ ВЕРИФИКАЦИЯ
доказывает, что полученный алгоритм обладает некоторыми свойствами, однако не гарантирует, что он в точности соответствует своему назначению.

ОСНОВНЫЕ ПОДХОДЫ К КОРРЕКТНОМУ ПРОЕКТИРОВАНИЮ РЕАКТИВНЫХ АЛГОРИТМОВ
СИНТЕЗ
гарантирует точное соответствие между спецификацией требований к алгоритму и ее процедурной реализацией.

ОСНОВНЫЕ ПОДХОДЫ К КОРРЕКТНОМУ ПРОЕКТИРОВАНИЮ РЕАКТИВНЫХ АЛГОРИТМОВ
ДОКАЗАТЕЛЬНОЕ ПРОЕКТИРОВАНИЕ
доказывается корректность всех процедур проектирования, а также всех преобразований, выполняемых разработчиком в процессе интерактивного проектирования.

ЯЗЫКИ СПЕЦИФИКАЦИИ
Ω = {p1, …, pk} – ПРЕДИКАТНЫЕ СИМВОЛЫ
t – ПЕРЕМЕННАЯ, СО ЗНАЧЕНИЯМИ ИЗ Z
ВИД ФОРМУЛ СПЕЦИФИКАЦИИ : ∀t F(t)
ЯЗЫК L
F(t) – ФОРМУЛА, ПОСТРОЕННАЯ С ПОМОЩЬЮ
ЛОГИЧЕСКИХ СВЯЗОК ИЗ АТОМОВ ВИДА
p(t + k), где p ∈ Ω, k ∈ Z.

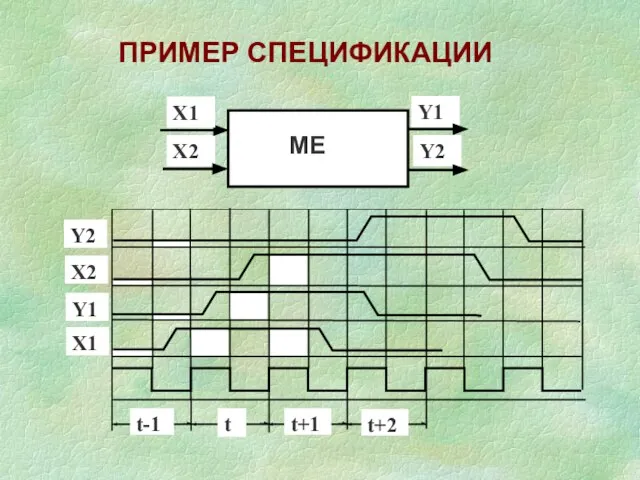
ПРИМЕР СПЕЦИФИКАЦИИ

{Y1(Y2) РАВЕН 1 ТОЛЬКО ТОГДА, КОГДА X1(X2) =1}
Y1(t) → X1(t) , Y2(t) → X2(t),
{СТАВ РАВНЫМ 1, Y1(Y2) СОХРАНЯЕТ ЭТО ЗНАЧЕНИЕ ,
ПОКА X1(X2) = 1}
Y1(t–1) & X1(t) → Y1(t),
Y2(t–1) & X2(t) → Y2(t),
{ВЗАИМНОЕ ИСКЛЮЧЕНИЕ}
¬(Y1(t) & Y2(t)),
{Y1(Y2) ИЗМЕНЯЕТСЯ В 1 ОДНОВРЕМЕННО С X1(X2)}
X1(t) → (Y1(t) ∨ Y2(t)),
X2(t) → (Y1(t) ∨ Y2(t)).
F = ∀tF(t)
ПРИМЕР СПЕЦИФИКАЦИИ

ЯЗЫК L*
ДОБАВЛЯЕТСЯ КОНСТРУКЦИЯ
∃t1(t1≤ t+k1)&F1(t1)&∀t2(t1+k2≤ t2≤ t+k3) → F2(t2),
F1(t1) – ФОРМУЛА ЯЗЫКА L*,
F2(t2) – ФОРМУЛА ЯЗЫКА L, k1, k2, k3∈ Z.

СВЕРХСЛОВА
ПУСТЬ σi ∈ Σ (i ∈ Z)
…σ-2σ-1σ0σ1σ2… – ДВУСТОРОННЕЕ
СВЕРХСЛОВО ( ΣZ )
σ1σ2… – СВЕРХСЛОВО ( Σω)
…σ-2σ-1 σ0 – ОБРАТНОЕ СВЕРХСЛОВО ( Σ– ω)
АЛФАВИТ Σ = {<00…0>, …, <11...1>}
Σ* – МНОЖЕСТВО ВСЕХ СЛОВ В АЛФАВИТЕ Σ

СВЕРХСЛОВА
ПУСТЬ k ∈ Z И u ∈ ΣZ
k-префикс u(– ∞, k) = …σk–2σk–1σk
k-суффикс u(k + 1, ∞) = σk+1σk+2…

АВТОМАТЫ
(X–Y) – АВТОМАТ A =
, ГДЕ
χA: Q × X × Y→ Q – ФУНКЦИЯ ПЕРЕХОДОВ,
Σ = X × Y
Σ-АВТОМАТ A = <Σ, Q, δA>, ГДЕ δA: Q × Σ → Q
СВЕРХСЛОВА И АВТОМАТЫ.
l = σ1σ2… ДОПУСТИМО В СОСТОЯНИИ q АВТОМАТА A, ЕСЛИ СУЩЕСТВУЕТ ТАКОЕ СВЕРХСЛОВО q0q1q2…,ГДЕ q0 = q, ЧТО ДЛЯ ЛЮБОГО i = 0, 1, 2,… δA(qi, σi+1) = qi+1.

АВТОМАТЫ
ПУСТЬ Q = {q1, …, qn} –
МНОЖЕСТВО СОСТОЯНИЙ АВТОМАТА A.
СЕМЕЙСТВО МНОЖЕСТВ (S1, …, Sn), ГДЕ Si – МНОЖЕСТВО ВСЕХ СВЕРХСЛОВ, ДОПУСТИМЫХ В СОСТОЯНИИ qi (i = 1, 2, …, n), НАЗЫВАЕТСЯ ПОВЕДЕНИЕМ АВТОМАТА A.

ФОРМУЛЫ И АВТОМАТЫ
ИНТЕРПРЕТАЦИЯ ЯЗЫКА
ПУСТЬ Ω = {p1, …, pk}
p1 …0110100…
. .
. . Σ = {<00…0>, …, <11...1>}
pk …1001110…
MF – МНОЖЕСТВО ВСЕХ МОДЕЛЕЙ ДЛЯ F,
WF – МН – ВО ВСЕХ 0-СУФФИКСОВ ИЗ MF ,
u ∈ MF Su = { l ∈ Σω | u(– ∞, 0)⋅l ∈ MF}
ℜF = {Su | u ∈ MF} = {S1, …, Sn}

ФОРМУЛЫ И АВТОМАТЫ
ФОРМУЛА F = ∀tF(t) СПЕЦИФИЦИРУЕТ АВТОМАТ A, ПОВЕДЕНИЕ КОТОРОГО СОВПАДАЕТ С
ℜF = {S1, …, Sn} .

ОСНОВНЫЕ ПРОЦЕДУРЫ ПРОЕКТИРОВАНИЯ
ПРОВЕРКА НЕПРОТИВОРЕЧИВОСТИ
ВЕРИФИКАЦИЯ СПЕЦИФИКАЦИИ
ПРЕОБРАЗОВАНИЕ СПЕЦИФИКАЦИИ ВО МНОЖЕСТВО ДИЗЪЮНКТОВ
ПОСТРОЕНИЕ АВТОМАТА, ПРЕДСТАВЛЕННОГО МНОЖЕСТВОМ СОСТОЯНИЙ И ФУНКЦИЯМИ ПЕРЕХОДОВ И ВЫХОДОВ
ДЕТЕРМИНИЗАЦИЯ АВТОМАТА

ОСОБЕННОСТИ ПОДХОДА
ОГРАНИЧЕННЫЙ СИНТАКСИС ЯЗЫКА
СПЕЦИФИКАЦИИ
ИНТЕРПРЕТАЦИЯ ЯЗЫКА НА МНОЖЕСТВЕ ЦЕЛЫХ
ЧИСЕЛ
ИСПОЛЬЗОВАНИЕ МОДЕЛИ НЕИНИЦИАЛЬНОГО
АВТОМАТА ДЛЯ ПРЕДСТАВЛЕНИЯ РЕАКТИВНОГО
АЛГОРИТМА