Содержание
- 2. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Доказательство через подобные треугольники.
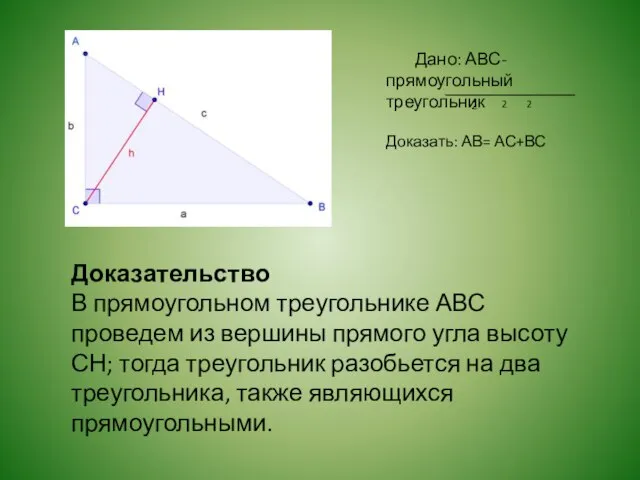
- 3. Дано: АВС- прямоугольный треугольник Доказать: АВ= АС+ВС 2 2 2 Доказательство В прямоугольном треугольнике АВС проведем
- 4. Треугольник ACH подобен треугольнику ABC по двум углам (по первому признаку подобия: если два угла одного
- 5. Теорема доказана. Пользуясь терминами теории пропорций: В прямоугольном треугольнике каждый катет есть средняя пропорциональная между гипотенузой
- 6. Мы пришли к доказательству теоремы Пифагора, основанному на теории подобия. Оно встречается у индуса Басхара (род.
- 7. Задачи на применение теоремы Пифагора
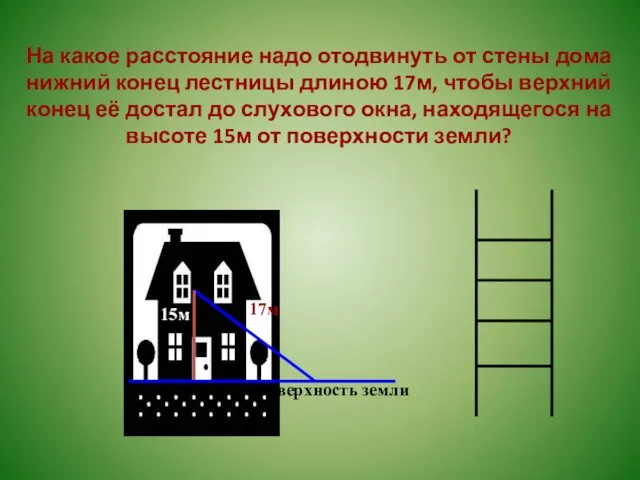
- 8. На какое расстояние надо отодвинуть от стены дома нижний конец лестницы длиною 17м, чтобы верхний конец
- 9. На какое расстояние надо отодвинуть от стены дома нижний конец лестницы длиною 17м, чтобы верхний конец
- 10. Задача древних индусов Над озером тихим, С полфута размером, высился лотоса цвет. Он рос одиноко. И
- 11. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И
- 13. Скачать презентацию








 Евангелие, которое мы проповедуем
Евангелие, которое мы проповедуем Введение. Основы безопасности жизнедеятельности
Введение. Основы безопасности жизнедеятельности СТОП вырубке ёлок!
СТОП вырубке ёлок! Тарифы курса Убеждения на миллион
Тарифы курса Убеждения на миллион Institute for Materials Science Problems n. I.N.Frantsevich NAN of the UkraineDiamond -hardalloy macrocomposit high-modulus material brand AVKM
Institute for Materials Science Problems n. I.N.Frantsevich NAN of the UkraineDiamond -hardalloy macrocomposit high-modulus material brand AVKM Поздравление от 5 «А»
Поздравление от 5 «А» Автомобили Франции
Автомобили Франции  Родительское собрание ТЕМА: «Служба школьной медиации»
Родительское собрание ТЕМА: «Служба школьной медиации» ЗИЛ-4421 1994г.в., дв. ЯМЗ-236 Полуприцеп ОДАЗ-885, 1980 г.в. УТС, цена 150 000 р. Торг. г. Барабинск, ул. Коммунистическая - 1 Т. (383) 289-25-23.
ЗИЛ-4421 1994г.в., дв. ЯМЗ-236 Полуприцеп ОДАЗ-885, 1980 г.в. УТС, цена 150 000 р. Торг. г. Барабинск, ул. Коммунистическая - 1 Т. (383) 289-25-23. Проект о скидках в процентах под Новый Год на Сотовую связь
Проект о скидках в процентах под Новый Год на Сотовую связь Правописание приставок
Правописание приставок ПРОБЛЕМА ВНЕДРЕНИЯ СТАНДАРТОВ ВТОРОГО ПОКОЛЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫЕ ШКОЛЫ
ПРОБЛЕМА ВНЕДРЕНИЯ СТАНДАРТОВ ВТОРОГО ПОКОЛЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫЕ ШКОЛЫ Географическая оболочка
Географическая оболочка Kursus «Tehniline analuus»maht: 1 ON
Kursus «Tehniline analuus»maht: 1 ON Конкурс ведущих
Конкурс ведущих The Finest of Fine Teas
The Finest of Fine Teas Тепловые насосы BROS
Тепловые насосы BROS Презентация на тему Принципы гражданского и арбитражного процесса
Презентация на тему Принципы гражданского и арбитражного процесса План развития сетей на 2018-2019 г
План развития сетей на 2018-2019 г Презентация на тему Дикие и домашние животные (3 класс)
Презентация на тему Дикие и домашние животные (3 класс) Презентация на тему Основные понятия компьютерной графики
Презентация на тему Основные понятия компьютерной графики  проф. С.В. Шалаев
проф. С.В. Шалаев 1. АПС 2020
1. АПС 2020 СТАТИСТИКА ЭНЕРГЕТИКИ УКРАИНЫ: ГАЗ ПРИРОДНЫЙ Баку, Азербайджан 27-28 сентября 2011 Анатолий Фризоренко Директор департамента ст
СТАТИСТИКА ЭНЕРГЕТИКИ УКРАИНЫ: ГАЗ ПРИРОДНЫЙ Баку, Азербайджан 27-28 сентября 2011 Анатолий Фризоренко Директор департамента ст Государственно-политическое развитие Великобритании в 17-19 вв. Становление в Англии конституционной монархии
Государственно-политическое развитие Великобритании в 17-19 вв. Становление в Англии конституционной монархии Запас вооруженных сил РФ
Запас вооруженных сил РФ Псевдо-конфликт. Факт-конфликт. Эго-конфликт
Псевдо-конфликт. Факт-конфликт. Эго-конфликт Felting exhibition(выставка из фетровых изделий)
Felting exhibition(выставка из фетровых изделий)