1,6, на величину большую 0,4 в обе стороны (и большую, и меньшую) равна:
Вероятность отклонения в одну (большую) сторону будет не более:
Итак, вероятность восстановления предприятием своей платежеспособности и возврата долга инвестору равна не более 6,25%. Значит, вероятность противоположного события, когда инвестор потеряет свои средства, вложенные в ненадежное предприятие, будет равна не меньше.
Достоинством неравенства Чебышева является то, что на его использование не накладывается каких-либо ограничений в части вида распределения вероятностей и объема исходных данных.







 Личность и ее социализация
Личность и ее социализация Власть и народ в стихотворении Н.А. Некрасова «Железная дорога»
Власть и народ в стихотворении Н.А. Некрасова «Железная дорога» Гордость и эгоизм
Гордость и эгоизм Паустовский Константин Сергеевич (3 класс)
Паустовский Константин Сергеевич (3 класс)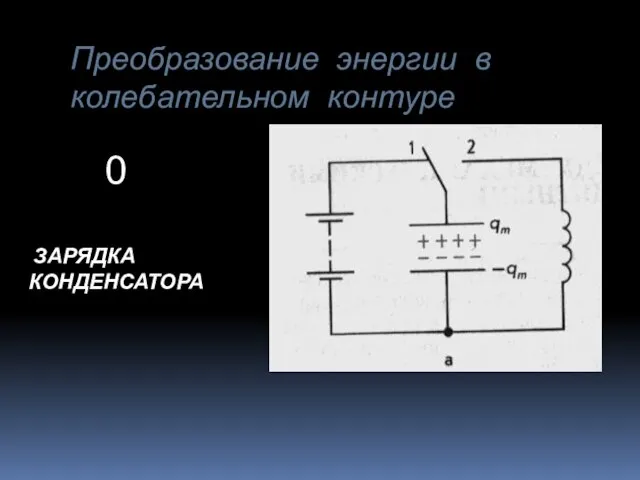 Презентация на тему Преобразование энергии в колебательном контуре
Презентация на тему Преобразование энергии в колебательном контуре  Слова благодарности выпускников учителям и родителям
Слова благодарности выпускников учителям и родителям МЕТОДЫ ОБУЧЕНИЯ
МЕТОДЫ ОБУЧЕНИЯ Основные ошибки при подаче документов на лицензирование
Основные ошибки при подаче документов на лицензирование Молодежная музыкальная Культура
Молодежная музыкальная Культура Дизайн вещно-пространственной среды жилища
Дизайн вещно-пространственной среды жилища Тутанхамон
Тутанхамон Ответственные родители
Ответственные родители Паттерн «Specification»
Паттерн «Specification» Композитинг
Композитинг ОСНОВНЫЕ ЦЕННОСТИ БРЕНДА «ТОРЭКС»
ОСНОВНЫЕ ЦЕННОСТИ БРЕНДА «ТОРЭКС» План Путина – победа России
План Путина – победа России Генрих Гейне (13 декабря 1797 -17 февраля 1856)
Генрих Гейне (13 декабря 1797 -17 февраля 1856) НАШИ РЕСУРСЫ РАЗВИТИЯ
НАШИ РЕСУРСЫ РАЗВИТИЯ Герои войны - дети
Герои войны - дети Коммерческая деятельность
Коммерческая деятельность My Trip to the UK
My Trip to the UK Мотивация кураторов и старших операторов
Мотивация кураторов и старших операторов Психологическая готовность детей к школе
Психологическая готовность детей к школе Компетенции сотрудников в краткосрочном проекте
Компетенции сотрудников в краткосрочном проекте Доступный спорт на открытом воздухе для жителей Старой Ржевки
Доступный спорт на открытом воздухе для жителей Старой Ржевки API WebMoney Transfer Для интернет-проектов. WebMoney как провайдер идентификации -11 млн зарегистрированных клиентов; - 4 уровня аттестации; - авт
API WebMoney Transfer Для интернет-проектов. WebMoney как провайдер идентификации -11 млн зарегистрированных клиентов; - 4 уровня аттестации; - авт НОРМЫ ПОВЕДЕНИЯ
НОРМЫ ПОВЕДЕНИЯ Зимний пейзаж
Зимний пейзаж