Движение

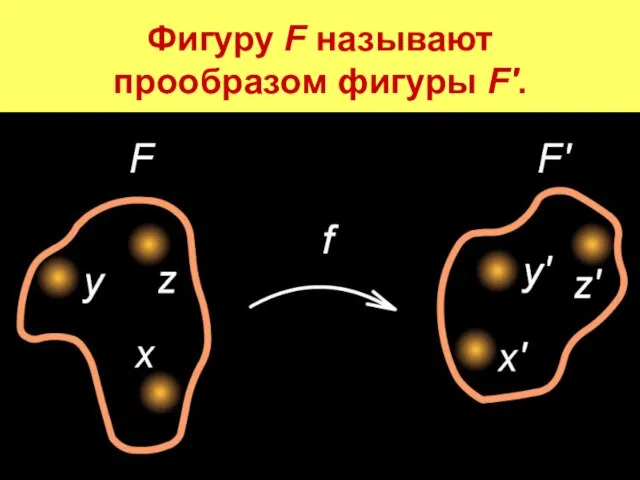
Фигуру F называют прообразом фигуры F'.

Преобразование фигуры, которое сохраняет расстояние между точками, называется движением этой фигуры

Свойства движения :
Точки, лежащие на одной прямой, при движении переходят в точки, лежащие на одной прямой.
Точки, не лежащие на одной прямой, при движении переходят в точки, не лежащие на одной прямой.
Отрезок переводится в отрезок, луч – в луч, прямая – в прямую.
Треугольник переводится в треугольник.
При движении сохраняются углы.
Фигура переходит в равную ей фигуру.

Формы движения:
параллельный перенос;
поворот;
симметрия относительно точки;
симметрия относительно прямой.

Параллельный перенос
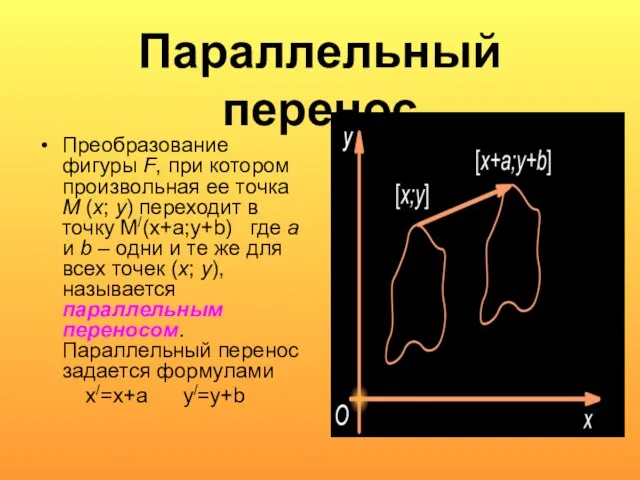
Преобразование фигуры F, при котором произвольная ее точка M (x; y) переходит в точку М/(х+а;у+b) где a и b – одни и те же для всех точек (x; y), называется параллельным переносом. Параллельный перенос задается формулами
x/=x+a y/=y+b

Поворот
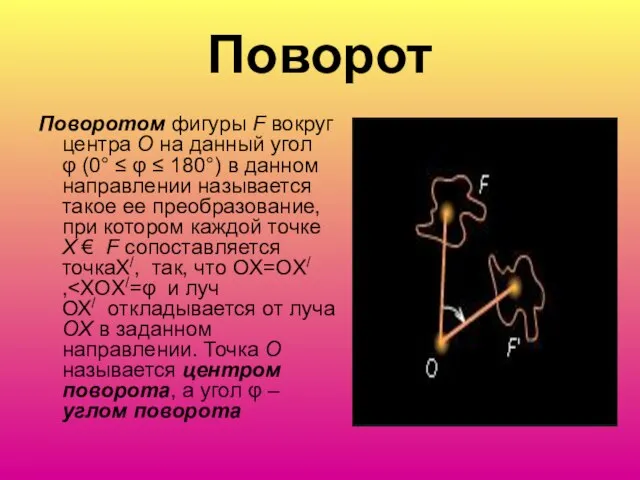
Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°) в данном направлении называется такое ее преобразование, при котором каждой точке X € F сопоставляется точкаX/, так, что OX=OX/ ,

Симметрия относительно точки
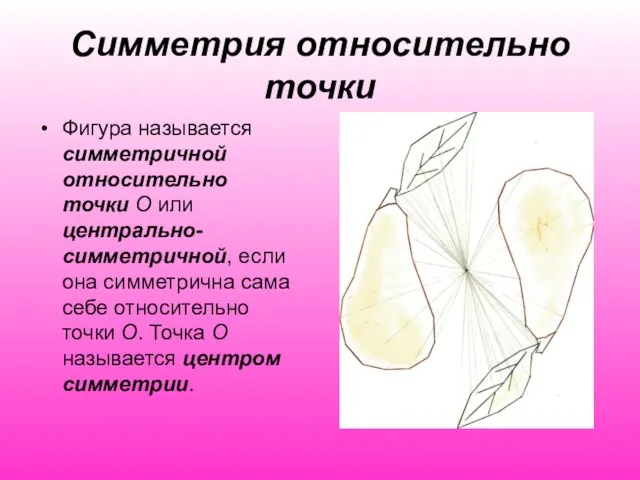
Фигура называется симметричной относительно точки O или центрально-симметричной, если она симметрична сама себе относительно точки O. Точка O называется центром симметрии.

Симметрия относительно прямой
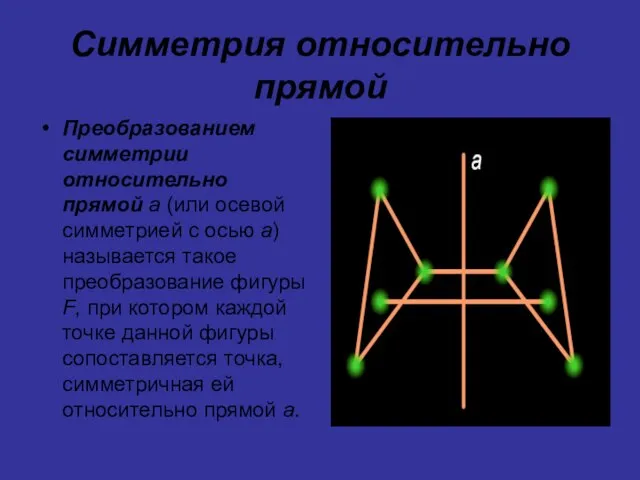
Преобразованием симметрии относительно прямой a (или осевой симметрией с осью a) называется такое преобразование фигуры F, при котором каждой точке данной фигуры сопоставляется точка, симметричная ей относительно прямой a.