Содержание
- 2. Повторим тему «Системы счисления»
- 3. Основные понятия систем счисления Система счисления - это способ записи чисел и связанные с ними способы
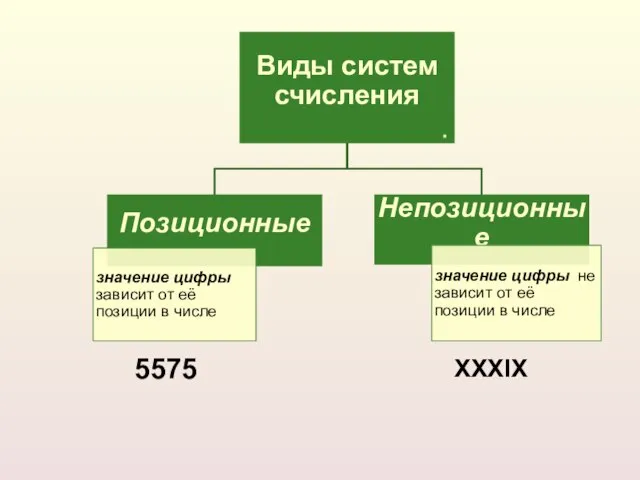
- 4. 5575 XXXIX
- 6. = 3 4 5
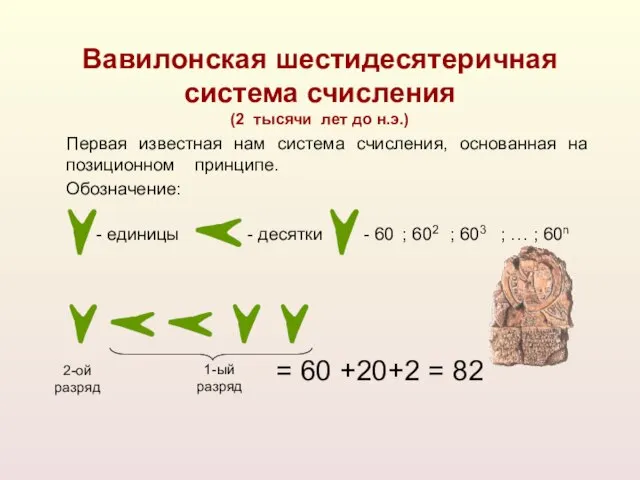
- 7. = 60 +20+2 = 82
- 8. X X X I I = 32 D X L I I = 542 Значение цифры
- 9. – основание (p) Набор всех цифр для записи числа – алфавит Количество цифр для записи числа
- 10. Алфавиты систем счисления Для записи чисел в позиционной системе с основанием р нужно иметь алфавит из
- 11. Представление информации в компьютере В каждой такой «клетке» хранится только одно из двух значений : нуль
- 12. 5555=5000+500+50+5=5*1000+5*100+5*10+5*1=5*103+5*102+5*101+5*100 456327=4*100000+5*10000+6*1000+3*100+2*10+7*1=4*105+5*104+6*103+3*102+2*101+7*100 Рассмотрим десятичную систему счисления Развёрнутая форма записи числа
- 13. Позиция цифры в числе называется разрядом. Aq = an-1qn-1 + … + a1q1 + a0q0 +
- 14. 11012=1*23+1*22+0*21+1*20=1*8+1*4+0*2+1*1=13 111000112=? Рассмотрим двоичную систему счисления Перевод двоичного числа в десятичное
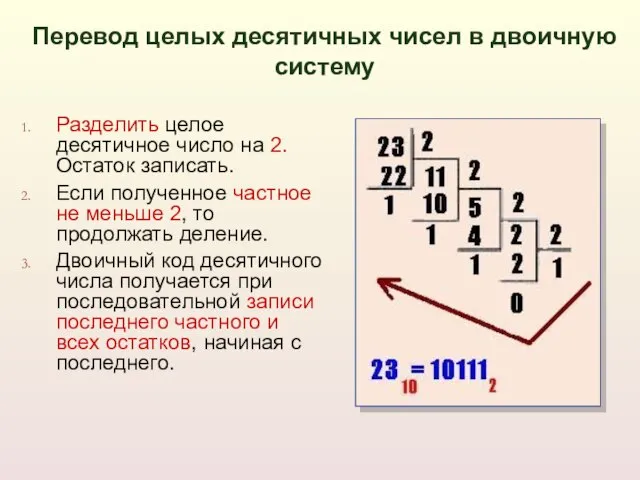
- 15. Разделить целое десятичное число на 2. Остаток записать. Если полученное частное не меньше 2, то продолжать
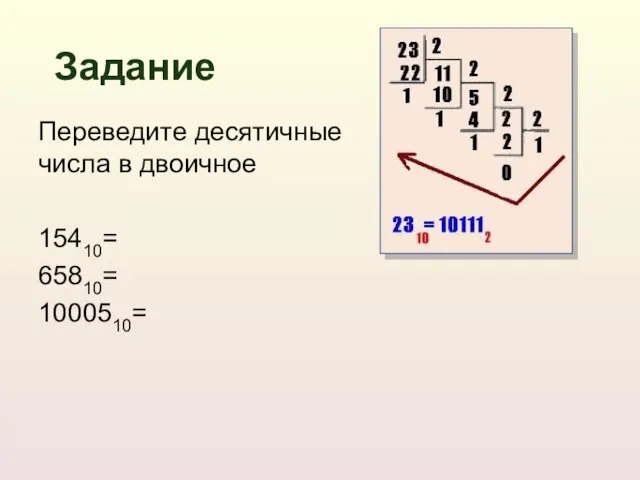
- 16. Переведите десятичные числа в двоичное 15410= 65810= 1000510= Задание
- 17. Арифметика двоичных чисел 0+0= 0+1= 1+0= 1+1= 0*0= 0*1= 1*0= 1*1= 0 10 0 0 0
- 19. Скачать презентацию












 Повторяем тему «Правила вычисления производной»
Повторяем тему «Правила вычисления производной» Занятие № 3 Речевые средства общения
Занятие № 3 Речевые средства общения Конституция ДНР
Конституция ДНР Основы композиции. Практическая работа
Основы композиции. Практическая работа Объявление онлайн-опрос ОМС
Объявление онлайн-опрос ОМС Презентация на тему Санкт-Петербург в романе: «Преступление и наказание». Современный Санкт-Петербург
Презентация на тему Санкт-Петербург в романе: «Преступление и наказание». Современный Санкт-Петербург  Концепция социально-экономического развития автономного округа
Концепция социально-экономического развития автономного округа Февральская лазурь
Февральская лазурь Разработка и пилотное внедрение административных регламентов исполнения государственных функций и административных регламенто
Разработка и пилотное внедрение административных регламентов исполнения государственных функций и административных регламенто Как сохранить здоровье?
Как сохранить здоровье? Обобщающее повторение фонетики, графики, орфоэпии и орфографии
Обобщающее повторение фонетики, графики, орфоэпии и орфографии Памятка студенту УниКИТа
Памятка студенту УниКИТа История отечественной художественной культуры
История отечественной художественной культуры Соловецкий монастырь- северное чудо России
Соловецкий монастырь- северное чудо России фруктовый фейерверк
фруктовый фейерверк Алгоритм ведения работы по контракту на оказание услуг по организации питания и обеспечению питьевого режима обучающихся
Алгоритм ведения работы по контракту на оказание услуг по организации питания и обеспечению питьевого режима обучающихся Презентация на тему Архимедова сила
Презентация на тему Архимедова сила  Основы уголовного права
Основы уголовного права Акцизы. Лекция 5
Акцизы. Лекция 5 Методический подход к духовно-нравственному воспитанию в работе Начертание христианского нравоучения
Методический подход к духовно-нравственному воспитанию в работе Начертание христианского нравоучения Проект Чертежник
Проект Чертежник Why I need study economics
Why I need study economics Роль и последствия экономической реформы 1965-1967 гг
Роль и последствия экономической реформы 1965-1967 гг Настольный теннис
Настольный теннис Химия элементов VIB подгруппы Cr, Mo, W
Химия элементов VIB подгруппы Cr, Mo, W Приспособленность городов России и городов Европы к велосипедам
Приспособленность городов России и городов Европы к велосипедам ФУНКЦИИ internet explorer 8
ФУНКЦИИ internet explorer 8 Привычки полезные и вредные
Привычки полезные и вредные